一个正方体和一个长方体拼成一个新的长方体,拼成的长方体的表面积比原来的长方体的表面积增加了50平方米。原来正方体的表面积是多少平方厘米?
题目
一个正方体和一个长方体拼成一个新的长方体,拼成的长方体的表面积比原来的长方体的表面积增加了50平方米。原来正方体的表面积是多少平方厘米?
相似考题
更多“一个正方体和一个长方体拼成一个新的长方体,拼成的长方体的表面积比原来的长方体的表面积增加了50平方米。原来正方体的表面积是多少平方厘米?”相关问题
-
第1题:
一个体积为l立方米的立方体,把它切成1立方厘米的小正方体,然后把这些小正方体排成一列,组成一个长方体。这个长方体长多少厘米?( )
A.10
B.1000000
C.200
D.1000
正确答案:B1立方米的正方体可以切割成1000000个1立方厘米的正方体,此时切割成的小正方体的边长为1厘米,则1000000个小正方体排成的长方体的长为1000000厘米。
-
第2题:
一个长方体的长、宽、高恰好是三个连续的自然数,并且它的体积数值等于它的所有 棱长之和的2倍,那么这个长方体的表面积是多少?( ) A.74 B.148 C.150 D.154
正确答案:B
本题属于几何问题。设宽为x,那么长为x+1,高为x-1,所有棱长之和为4×3x=12x,体积为x(x+1)(x-1),根据题意2×12x=x(x+1)(x-1),解得x=5。所以长为6,高为4。表面积=2×(4×5+4×6+5×6)=148。故选B。
-
第3题:
一个长方体前面和上面的面积和是209平方厘米。如果这个长方体的长、宽、高都是以厘米为单位的质数,那么这个长方体的体积是多少立方厘米?
A.209
B.342
C.374
D.418
正确答案:
设长、宽、高分别为x、y、z厘米,则x(y+z)=209=11×19。
由于11和19都是奇数。说明y和z之间必然有一个偶数,而y、z都是质数,故其中一个数是2,不妨设z=2。若y+z=11,则y=9,不为质数,矛盾。因此,y+z=19,y=17,x=11。
该长方体体积为11×17×2=374立方厘米。
-
第4题:
用n个棱长是a cm的小正方体可以摆出“一”字形长方体,如图,n个小正方体拼在一起 时,这个长方体表面积是_______cm2。
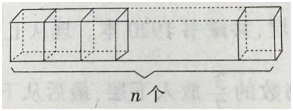 答案:解析:(4n+2)a2。解析:n个小正方体如题干图中所示拼在一起时,组成长为na,宽为a,高为a的长方体,所以表面积为(4n+2)a2 cm2。
答案:解析:(4n+2)a2。解析:n个小正方体如题干图中所示拼在一起时,组成长为na,宽为a,高为a的长方体,所以表面积为(4n+2)a2 cm2。 -
第5题:
把一个64cm×40cm×24cm的长方体切成若干个完全相同的小正方体,并使这些小正方体的表面积总和最小,则小正方体的表面积总和为()。A.73280cm2
B.54680cm2
C.69450cm2
D.46080cm2答案:D解析:要使这些小正方体的表面积总和最小,那么小正方体的边长要尽可能大。64、40、24的最大公约数为8,因此小正方体的边长为8cm,共有64×40×24÷83=120块。表面积总和为6×82×120=46080cm2. -
第6题:
210个边长为1厘米的小正方体组成的长方体,其表面积最小为多少?( )A.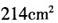
B.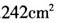
C.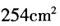
D.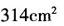 答案:A解析:该长方体体积为210立方厘米,根据体积一定的情况下越接近球体表面积越小,则其长、宽、高应尽量接近。210=2×3×5×7,当三个棱长分别为5、6、7时,表面积最小是2×(5×6+5×7+6×7)=214平方厘米。
答案:A解析:该长方体体积为210立方厘米,根据体积一定的情况下越接近球体表面积越小,则其长、宽、高应尽量接近。210=2×3×5×7,当三个棱长分别为5、6、7时,表面积最小是2×(5×6+5×7+6×7)=214平方厘米。 -
第7题:
将一个表面积为36平方米的正方体等分成两个长方体,再将这两个长方体拼成一个大长方体,则大长方体的表面积是( )。A. 24平方米
B. 30平方米
C. 36平方米
D. 42平方米答案:D解析:将原正方体等分后重新组合,则表面积必然会比原来的大,所以D项正确。故答案为D。 -
第8题:
小学数学《长方体和正方体的体积》
一、考题回顾

 答案:解析:二、考题解析
答案:解析:二、考题解析
【教学过程】
(一)导入新课
教师创设情境:家里新买了一个冰箱。提出问题:冰箱是一个什么形状的几何图形?如何知道它的体积?
引出课题。
(二)新知探索
提出问题并引导学生思考:长方体各个面都是什么形状的?我们该如何研究它的大小的?
学生根据老师的提示想到长方形是用一个个面积相等的小正方形来测量长方形的面积。
提出问题:类比长方形测量面积的方式,如何知道长方体的体积呢?
组织学生小组讨论。
预设1:可以将长方体切成大小相同的小正方体。
预设2:之前计算长方形的面积直接测量长和宽,那长方体的体积能不能先测量再计算出体积呢?
教师组织学生前后桌四人为一组,用体积为1cm3的小长方体摆成不同的长方体。在交流中思考:如何摆放?长宽高分别是多少,长方体的体积是多少?并完成学案上的表格。


【答辩题目解析】
1.长方体正方体的体积是如何探究的?
【参考答案】
本节课先带领学生回顾之前是如何求得长方形的面积的,类比长方形用小正方形作为面积单位,长方体就可以用小正方体作为体积单位,观察其中包含几个小正方体。接下来组织探究活动,学生根据手中拿到的小正方体拼成长方体,观察研究发现长方体的体积可以计算包含多少个体积单位计算,还发现长方体的体积就等于长×宽×高。师生共同总结长方体体积公式并根据长方体和正方体的关系得到正方体体积公式。
2.在本节课中,教学重难点是什么?
【参考答案】
教学重点:长方体正方体的体积公式。
教学难点:长方体正方体体积公式探究过程。 -
第9题:
一个长方体木块恰能切割成五个正方体木块,五个正方体木块表面积之和比原来的长方体木块的表面积增加了200cm2。则长方体木块的体积为多少?A.625cm3
B.125cm3
C.500cm3
D.750cm3答案:A解析:第一步,本题考查几何问题,属于立体几何类。
第二步,如图所示,长方体分为5个小正方体,增加了4×2=8(个)阴影部分小正方形的面积,则每个小正方形面积为200÷8=25(cm2),边长为5cm。那么大长方体的体积为5×25×5=625(cm3)。
因此,选择A选项。 -
第10题:
将一个表面积为72平方米的正方体平分为两个长方体,再将这两个长方体拼成一个大长方体,则大长方体的表面积是多少平方米?A.56
B.64
C.72
D.84答案:D解析:第一步,本题考查几何问题,属于立体几何类。
第二步,如下图所示,立方体变为长方体。正方体一个面面积为72÷6=12(平方米),则表面积的变化为:增加了两个侧面为12×2=24(平方米),侧面的一半减少了两个,减少了12÷2×2=12(平方米)。故最终增加了24-12=12(平方米),表面积为72+12=84(平方米)。

-
第11题:
以下哪个选项适合作为五年级下册《长方体和正方体的表面积》教学的知识目标?()
- A、让学生理解长方体和正方体的表面积意义,初步学会长方体和正方体面积的计算方法
- B、通过小组合作、观察思考等解决问题的方法
- C、让学生感受到数学与生活的密切联系
- D、培养学生探求意识和探求能力
正确答案:A -
第12题:
把一个64Cmx40Cmx24Cm的长方体切成若干个完全相同的小正方体,并使这些小正方体的表面积总和最小,则小正方体的表面积总和为( )。
A.73280cm2
B.54680cm2
C.69450cm2
D.46080cm2
正确答案:D
要使这些小正方体的表面积总和最小,那么小正方体的边长要尽可能大。64、40、24的最大公约数为8,因此小正方体的边长为8cm,共有64×40×24÷83=120块。表面积总和为6×82×120=46080cm2。 -
第13题:
边长为1米的正方体525个,堆成了一个实心的长方体,它的高是5米,长、宽都大于高,问长方体的长与宽的和是多少米?
A.21
B.22
C.23
D.24
正确答案:B
525=5×105=5×3×5×7=5×7×15,所以长和宽分别为15米和7米,它们的和为22米。 -
第14题:
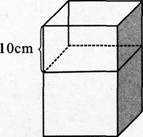
一个正方体的高增加10cm,得到新长方体的表面积比原正方体表面积增加120cm,原正方体体积是( ).A.9cm3
B.12cm3
C.18cm3
D.27cm3答案:D解析:如下图所示,高增加10cm后,增加的表面积为四个侧面积.设原正方体的棱长为acm,则有4×10a=120,解得a=3,则原正方体的体积为33=27cm3.
-
第15题:
210个边长为1cm的小正方体组成的长方体,其表面积最小为多少?( )A.214c㎡
B.242c㎡
C.254c㎡
D.314c㎡答案:A解析: -
第16题:
长方体的表面积是88,其长、宽、高之比为3:2:1,则长方体的体积是:( )A.48
B.46
C.384
D.3072答案:A解析:
-
第17题:
将一个表面漆有红色的长方体分割成若干个体积为1立方厘米的小正方体,其中,一点红色也没有的小正方体有4块,那么原来的长方体的体积为( )立方厘米A.180
B.54
C.54或48
D.64
E.180或64答案:C解析:没有红色的小正方体位于原来的长方体的内部,这4个小正方体可能排成一字形或田字形;若为一字形:棱长分别为1,1,4,故原长方体的长宽高为3,3,6,体积为3×3×6=54;若为田字形:棱长分别为2,2,1,故原长方体的长宽高为4,4,3,体积为4×4×3=48 -
第18题:
小学数学《长方体和正方体的表面积》
一、考题回顾
题目来源:5月18日 上午 天津市 面试考题
试讲题目
1.题目:长方体和正方体的表面积
2.内容:


3.基本要求:
(1)10分钟试讲;
(2)引导学生理解长方体和正方体的表面积计算公式;
(3)要有适当板书。
答辩题目
1.本节课的教学目标是什么?
2.如何做好课堂提问?答案:解析:二、考题解析
【教学过程】
(一)导入新课
课件出示:丰富的生活场景;一些长方体、正方体纸盒;漂亮的礼品盒。
提出问题:
(1)前面我们看到的主要是什么形状的物体?
(2)单独出示一个漂亮的礼品盒(出示图:长6厘米、宽5厘米、高4厘米)。想做一个这样的纸盒,至少需要多少硬纸板?
引出课题。
(二)新知探索
1.表面积的概念
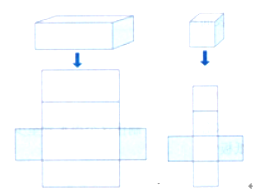
提问:如果把手中的长方体纸盒、正方体纸盒展开会是什么样子呢?
学生操作,得出如下图:
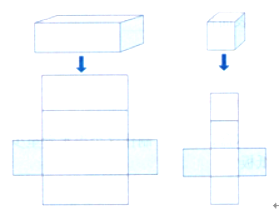
引导学生小组合作,在展开图中标出原来长方体、正方体的上、下、前、后、左、右6个面,并观察。
提问:哪些面的面积相等?每个面的长和宽与长方体的长宽高有什么关系?
预设:长方体的上下面积、前后面积、左右的面相等。正方体的六个面都相等。
教师给出表面积的概念:长方体或正方体6个面的总面积,叫做它的表面积。
2.表面积公式
例1:做一个微波炉的包装箱,至少需要多少平方米的硬纸板?

引导学生表示出上下、前后、左右面的面积,得出长方体表面积的计算方法。
例2:一个正方体墨水盒,棱长为6.5cm。制作这个墨水盒至少需要多少平方厘米的硬纸板?

引导学生通过合作,自己去探求正方体表面积的计算方法,通过对微波炉的包装,引导学生掌握正确计算长方体面积的计算方法。
总结:长方体表面积=(长×宽+长×高+宽×高)×2;正方体表面积=边长×边长×6
(三)课堂练习
做一做题目:
要做这样一个衣柜的布罩,至少需要用布多少平方米?
(四)小结作业
这节课我们一起学习了什么?你有哪些收获?
利用本节课所学的知识解决生活中遇到的问题。
【板书设计】
长方体和正方体的表面积
长方体或正方体6个面的总面积,叫做它的表面积。
例1:
例2:
长方体表面积=(长×宽+长×高+宽×高)×2;正方体表面积=边长×边长×6
【答辩题目解析】
1.本节课的教学目标是什么?
【参考答案】
知识与技能:能够知道什么是长方体和正方体表面积,学会长方体和正方体表面积计算方法,并能够运用方法解决实际问题。
过程与方法:通过动手实践、自主探索和合作交流的学习方式参与活动之中探索本质,锻炼分析、归纳、概括、推理能力。
情感态度与价值观:经历过程体验成功,激发学习兴趣,树立自信,形成良好的学习习惯。
2.如何做好课堂提问?
【参考答案】
课堂提问是启发学生非常重要的手段。要想做好,需要从以下几个方面入手:
首先,深钻教材是有效提问的前提。教师只有钻研教材,把握知识的来龙去脉,教学目标才能明确,教学重难点才能清晰,提问才能更具有针对性。
其次,教师需要了解学生情况。了解学生的生活经验,了解学生的知识背景,了解学生已有的知识与技能水平,这样才能依据学生情况提出更有针对性的问题,实现有效提问。
然后,教师还要合理设计提问的问题。把握好问题的形式。
最后,提问应该给予学生足够的思考与反应时间,才能达到最好的效果。 -
第19题:
边长为1米的正方体525个,堆成了一个实心的长方体,它的高是5米,长、宽都大于高,则长方体的长与宽的和是多少米?( )
A. 21
B. 22
C. 23
D. 24答案:B解析:解题指导: 根据题意得,实心长方形的体积为525立方米,又因为高为5米,故长*宽=105立方米,又因105=5*3*7,且长,宽均大于高,因此长为15,宽为7,则长与宽的和为15+7=22米。故答案为B。 -
第20题:
210个边长为1厘米的小正方体组成的长方体,其表面积最小为多少?
A.214cm2
B.242cm2
C.254cm2
D.314cm2答案:A解析:该长方体体积为210立方厘米,根据体积一定的情况下越接近球体表面积越小,则其长、 宽、高应尽量接近。210=2x3x5x7,当三个棱长分别为5、6、7时,表面积最小是2x(5x6+5x7+6x7)=214平方厘米。 -
第21题:
一个长方体的长、宽、高分别是a米、b米、h米,如果高增加3米后,新的长方体体积比原来增加()立方米。
- A、3ab
- B、3abh
- C、ab(h+3)
- D、abh+33
正确答案:A -
第22题:
有一个棱长为1米的立方体,沿长、宽、高分别切三刀、四刀、五刀后,切成了若干个相同的小长方体,问这些小长方体的表面积总和是多少?()
- A、24
- B、30
- C、25
- D、35
正确答案:B
