itgle.com
甲、乙、丙三人跑步比赛，从跑道起点出发，跑了20分钟，甲超过乙一圈，又跑了10分钟，甲超过丙一圈，问再过多长时间，丙超过乙一圈（） A、30分钟B、40分钟C、50分钟D、60分钟
题目
甲、乙、丙三人跑步比赛，从跑道起点出发，跑了20分钟，甲超过乙一圈，又跑了10分钟，甲超过丙一圈，问再过多长时间，丙超过乙一圈（）
- A、30分钟
- B、40分钟
- C、50分钟
- D、60分钟
相似考题
更多“甲、乙、丙三人跑步比赛，从跑道起点出发，跑了20分钟，甲超过乙一”相关问题
-
第1题：
周长为400米的圆形跑道上， 有相距100米的A、B两点， 甲乙两人分别从A、B两点同时相背而跑， 两人相遇后， 乙即转身与甲同向而跑步， 当甲跑到A时， 乙恰好跑到B。如果以后甲、乙跑的速度方向都不变，那么甲追上乙时，甲从出发开始，共跑了( )米。
A．600
B．800
C．900
D．1000
正确答案：D
13．D【解析】乙从相遇点C跑回B点时，甲从C过B到A，他比乙多跑了100米，乙从B到C时， 甲从A到C， 说明A到C比B到C多100米， 跑道周长400米， 所以8到C是100米，A到C是200米，甲跑200米，比乙多100米。甲追上乙要多跑300=400—100(米)，所以甲要跑200X 3=600(米)，加上开始跑的一圈，甲共跑600+400=1000(米)。 -
第2题：
甲、乙、丙三人的跑步速度分别为8米／秒、6米／秒、18千米／时，他们沿同一环形跑道在同一起点同时同向出发，则到他们三人再次同时回到起点时，甲和丙一共相遇多少次?（ ） A．1次 B．2次 C．3次 D．4次
正确答案：C
丙的速度为18千米／时＝5米／秒，则甲、乙、丙的速度比为8：6：5，故三人同时回到起点时，甲跑了8圈，丙跑了5圈，甲比丙多跑3圈，即相遇了3次。故选C。
-
第3题：
某儿童娱乐场有两条圆形赛车跑道，大圆跑道直径80米，小圆跑道直径60米，两跑道于发车起点A处相切重合。假设甲、乙两辆车同时从A点以相同速度出发（甲跑大圈、乙跑小圈），且此后速度均保持不变。则第一次相距最远时，甲、乙各跑了（ ）圈。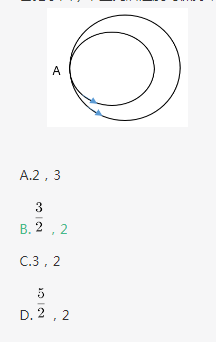
答案：B解析：第一步，本题考查行程问题，属于基本行程类，用代入排除法解题。
第二步，如图所示：乙在A处、甲在B处时，两车相距最远。此时，乙跑了整数圈，甲跑了
圈，排除A、C选项。
第三步，小圈周长60π、大圈周长80π。甲乙同时以相同速度出发，经相同时间，行驶路程相等：
-
第4题：
一个正方形跑道边长为20米，甲和乙从跑道上的不同位置同时出发，匀速沿逆时针跑步，已知两人出发的位置之间直线距离为20米，甲以2米/秒的速度跑6秒到达某个顶点后，又跑了不到10秒正好到达乙出发的位置，此时乙正好第二次跑到顶点位置。问以下哪个描述是正确的？（ ）A.甲出发后不到2分钟第一次追上乙
B.甲出发后超过2分钟第一次追上乙
C.乙出发后不到2分钟第一次追上甲
D.乙出发后超过2分钟第一次追上甲答案：A解析：本题属于行程问题。
由甲以2米/秒的速度跑6秒到达某个顶点，画出图示。如图所示：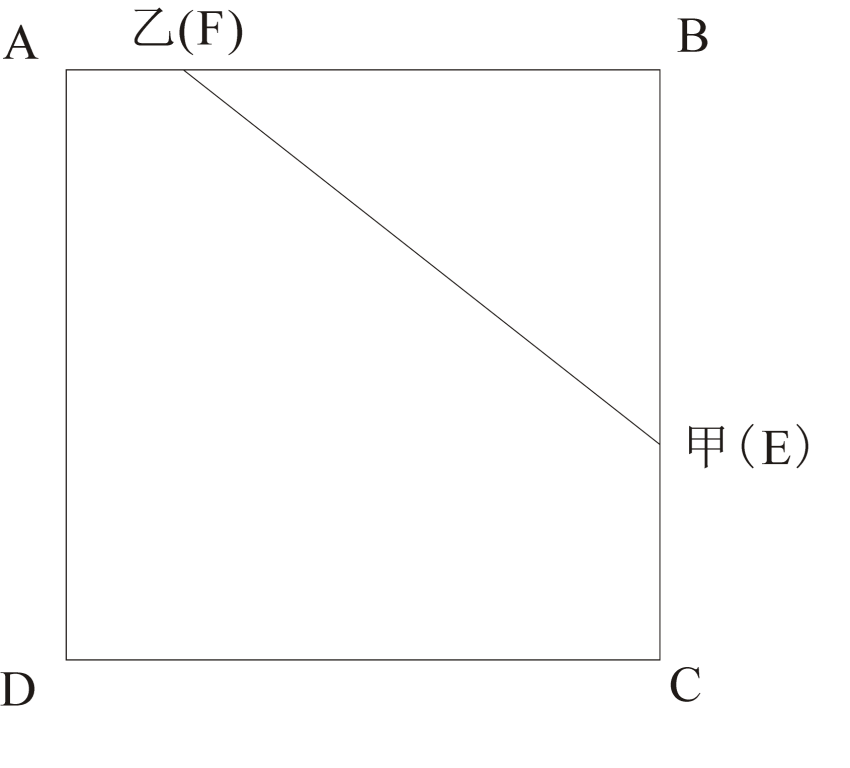
甲初始位置在E点，EB=6×2=12米，由题意又跑了不到10秒正好到达乙出发的位置，所以画出示意图乙出发点在F点，且EF=20。由勾股定理可求得BF=16。甲到达乙的出发点共用时（12+16）÷2=14秒。又因为此时乙正好第二次跑到顶点位置，即跑到了D点，所以乙的速度为（4+20）÷14=12/7。甲的速度大于乙的速度，所以甲出发后，追上乙需要的时间为（12+16）÷（2-12/7）=98s。A符合题意。
因此，选择A选项。 -
第5题：
甲、乙二人进行跑步比赛同时从起点出发后，当甲跑了全赛程的3/8时，乙跑了全赛程的1/3,以后甲的速度不变，乙提高了速度,结果两人同时到达了终点，问后来乙的速度提髙了多少？
a.12% b. 15% c. 18% d.20%答案：D解析：
-
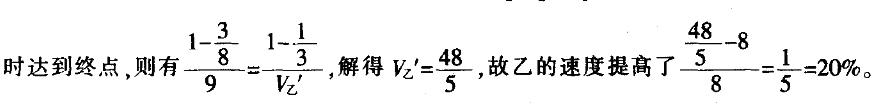
第6题：
甲、乙、丙三人跑步比赛，从跑道起点出发，跑了20分钟，甲超过乙一圈，又跑了10分钟，甲超过丙一圈，问再过多长时间，丙超过乙一圈（）
- A、30分钟
- B、40分钟
- C、50分钟
- D、60分钟
正确答案:A -
第7题：
单选题甲、乙、丙三人从400米环形跑道上三个前后等距的起点出发（甲在最后、丙在最前），沿顺时针方向跑步，三人的速度分别为8米／秒、6米／秒、4米／秒。为了保证三人同时到达终点（甲的起点），乙、丙又分别比甲提前一段时间出发，已知丙比乙提前10秒出发。求三人起点的间距为多少米？A50
B60
C70
D80
正确答案： B解析： -
第8题：
单选题甲、乙两名运动员在400米的环形跑道上练习跑步，甲出发1分钟后乙同向出发，乙出发2分钟后第一次追上甲，又过了8分钟，乙第二次追上甲，此时乙比甲多跑了250米，问两人出发地相隔多少米（ ）A200
B150
C100
D50
正确答案： A解析： -
第9题：
甲、乙、丙三人沿着400米环形跑道进行800米跑比赛，当甲跑1圈时，乙比甲多跑1/7圈。丙比甲少跑1/7圈。如果他们各自跑步的速度始终不变，那么，当乙到达终点时，甲在丙前面（ ）
正确答案：C
-
第10题：
甲、乙、丙三人沿圆形跑道跑步，同时从跑道某一固定点出发，甲按顺时针方向行走，乙与丙按逆时针方向行走，甲第一次遇到乙2分钟后遇到丙，再过8分钟第二次遇到乙。已知乙的速度是甲的2/3，圆形跑道的周长为600米，则丙的速度为( )。A. 14米/分
B. 15米/分
C. 16米/分
D. 17米/分答案：A解析：行程问题。在环形相遇问题中，任意两者相遇一次所走的路程和为一个周长，因此，甲与乙第二次相遇共走的路程（1200米）是第一次相遇共走的路程（600米）的2倍，由于二者速度不变，设第一次的相遇所用时间为t，则第二次相遇时间应为2t，根据题意有2t=t+2+8，解得t=10分钟。再设甲、乙、丙的速度分别为、、，则（+）×10=600，（+V丙）×（10+2）=600，又，解得=36米/分，=14米/分。故本题选择A。 -
第11题：
甲、乙、丙三人跑步比赛，从跑道起点出发，跑了20分钟，甲超过乙一圈，又跑了10分钟，甲超过丙一圈，问再过多长时间，丙超过乙一圈？A. 30分钟
B. 40分钟
C. 50分钟
D. 60分钟答案：A解析：列方程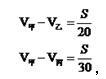
两式相减得到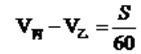
所以丙超过乙一圈需要60分钟，所以说再过30分钟即可，选择A选项。 -
第12题：
某市一体育场有三条同心圆的跑道，里圈跑道长公里，中圈跑道长公里，外圈跑道公里。甲、乙、丙三人分别在里、中、外圈同一起跑线同时同向跑步。甲每小时跑3.5公里，乙每小时跑4公里，丙每小时5公里，问几小时后三人同时回到出发点：
A8小时
B7小时
C6小时
D5小时答案：C解析：
-
第13题：
甲、乙两名运动员在400米的环形跑道上练习跑步，甲出发1分钟后乙同向出发，乙出发2分钟后第一次追上甲，又过了8分钟，乙第二次追上甲，此时乙比甲多跑了250米，问两人出发地相隔多少米（）
- A、200
- B、150
- C、100
- D、50
正确答案:B -
第14题：
单选题一条圆形跑道长500米，甲、乙两人从不同起点同时出发，均沿顺时针方向匀速跑步。已知甲跑了600米后第一次追上乙，此后甲加速20%继续前进，又跑了1200米后第二次追上乙。问甲出发后多少米第一次到达乙的出发点？（ ）A180
B150
C120
D100
正确答案： A解析：
赋值甲的速度为100米/分，第一次追及，甲跑了600米，用时为6分；第二次追及，甲加速20%，即速度为120米/分，又跑了1200米，用时为10分。行程问题追及公式为：S差＝v差t，从第一次追及开始，到第二次追及时，两人的路程差为1圈，即500＝（120－v乙）×10，解得v乙＝70米/分。分析第一次追及过程可知，甲比乙多走的距离即为甲出发点到乙出发点距离，S差＝v差t＝（100－70）×6＝180米。故正确答案为A。 -
第15题：
单选题甲每秒跑3米，乙每秒跑2米，丙每秒跑4米，三人沿600米的环形跑道从同一点同时同向跑步，经过()秒三人又同时从出发点出发。A12
B600
C300
D无法确定
正确答案： B解析： 暂无解析