itgle.com
编程实现用Euler法求初值问题的数值解，设方程如下：du/dt=√u+5u，且u（0）=1，t=[0，10]，并取步长h=0.1。
题目
编程实现用Euler法求初值问题的数值解，设方程如下：du/dt=√u+5u，且u（0）=1，t=[0，10]，并取步长h=0.1。
相似考题
参考答案和解析
正确答案:
t=0:0.1:10;
n=length(t);
h=0.1;
u(1)=1;
uu=1;
for i=2:n
du=(sqrt(uu)+5*uu)*h;
uu=uu+du;
u(i)=uu;
end
n=length(t);
h=0.1;
u(1)=1;
uu=1;
for i=2:n
du=(sqrt(uu)+5*uu)*h;
uu=uu+du;
u(i)=uu;
end
更多“编程实现用Euler法求初值问题的数值解，设方程如下：du/dt=√u+5u，且u（0）=1，t=[0，10]，并取步长h=0.1。”相关问题
-
第1题：
图中所示电路c=0.1F,R=10Ω,求冲击响应u为()。
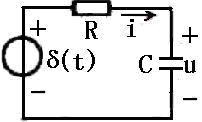
A、0
B、e-t1(t)V
C、其它
参考答案：B
-
第2题：
设X~N (μ,σ2),其中σ2已知，对假设检验问题H0： μ=μ0，H1: μ≠μ0的显著性水平为α的拒绝域为（ ）。
A. U 〉uα B. U 〉u 1-α
C. U 〉-u α/2 D. U 〉u α/2
E. t ＞t 1-α/2答案：C,D解析：。在σ已知时，选择U统计量，双侧原假设，选择1—α/2分位数。 -
第3题：
设A为三阶实对称矩阵,A的每行元素之和为5,AX=0有非零解且λ1=2是A的特征值,
对应特征向量为(-1,0,1)^T.
(1)求A的其他特征值与特征向量；
(2)求A.答案：解析：
-
第4题：
设随机变量X,y独立同分布,且X～N（0,σ^2）,再设U=aX+by,V=aX-bY,其中a,b为不相等的常数.求：
(1)E(U),E(V),D(U),D(V),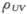
;
(2)设U,V不相关,求常数A,B之间的关系.答案：解析：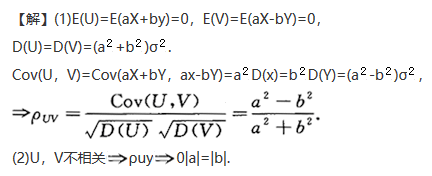
-
第5题：
设A=
，E为三阶单位矩阵.
(Ⅰ)求方程组Ax=0的一个基础解系；
(Ⅱ)求满足AB=E的所有矩阵B.答案：解析：【分析】(Ⅰ)是基础题，化为行最简即可.
关于(Ⅱ)中矩阵B，其实就是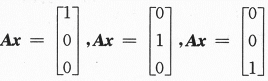
三个方程组的求解问题.
【解】(Ⅰ)对矩阵A作初等行变换，得
-
第6题：
已知方程组(I)
(II)图1} (1)a,b取什么值时这两个方程组同解?此时求解. (2)a,b取什么值时这两个方程组有公共解? 此时求公共解{答案：解析：
-
第7题：
设3阶实对称矩阵A的各行元素之和都为3,向量
都是齐次线性方程组AX=0的解.① 求A的特征值和特征向量.② 求作正交矩阵Q和对角矩阵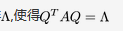
答案：解析：
-
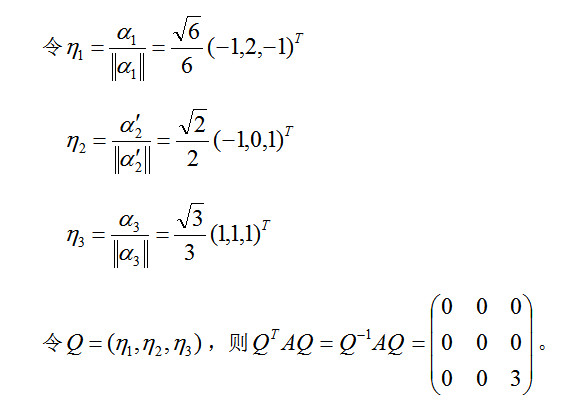
第8题：
设(Ⅰ)和(Ⅱ)都是个四元齐次方程组,已知(1,0,1,1)T,(-1,0,1,0)T,(0,1,1,0)T是(Ⅰ)的一个基础解系,(0,1,0,1)T,(1,1,-1,0)T是 (Ⅱ) 的一个基础解系．求(Ⅰ)和(Ⅱ)的公共解答案：解析：
-
第9题：
设(Ⅰ)和(Ⅱ)是两个四元齐次线性方程组,(Ⅰ)为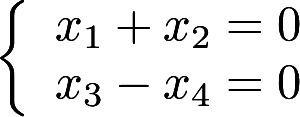
，(Ⅱ)有一个基础解系(0,1,1,0)T,(-1,2,2,1)T．求(Ⅰ)和(Ⅱ)的全部公共解答案：解析：
-
第10题：
常微分方程初值问题的数值解法有很多，比较常用的方法不包括（）。
- A、欧拉法
- B、龙格-库塔法
- C、线性多步法
- D、向量法
正确答案:D -
第11题：
问答题设AX=0与BX=0均为n元齐次线性方程组，秩r（A）=r（B），且方程组AX=0的解均为方程组BX=0的解，证明方程组AX=0与BX=0同解.正确答案：
设r(A)=r(B)=r,方程组AX=0的基础解系为①:ζ1,ζ2,…,ζn-r,方程组BX=0的基础解系为②:η1,η2,…,ηn-r.
构造向量组③:ζ1,ζ2,…,ζn-r,η1,η2,…,ηn-r.
由向量组①可由②线性表示,则向量组②和③等价,从而r(③)=n-r,所以ζ1,ζ2,…,ζn-r是向量组③的极大线性无关组,有η1,η2,…,ηn-r可由ζ1,ζ2,…,ζn-r线性表示,即BX=0的任一解都可由ζ1,ζ2,…,ζn-r线性表示,故BX=0的解都是AX=0的解,所以方程组AX=0与BX=0同解.解析： 暂无解析 -
第12题：
问答题设η(→)1，η(→)2，η(→)3，η(→)4是五元非齐次线性方程组AX(→)＝b(→)的四个解，且秩r（A）＝3，又设：η(→)1＋η(→)2＋η(→)3＋η(→)4＝（4，－8，－12，12，16）T，η(→)1＋2η(→)2＋2η(→)3＋η(→)4＝（6，18，－18，－30，12）T，2η(→)1＋2η(→)2＋η(→)3＋η(→)4＝（18，－30，－36，30，36）T，求方程组AX(→)＝b(→)的通解。正确答案：
由系数矩阵A的秩r(A)=3,知五元线性方程组的基础解系应含两个解向量。
由线性方程组解的性质知η2-η1,η3-η4,η1-η3,η2-η4都是其导出组的解,且它们的组合也是导出组的解,所以有
ξ1=(η2-η1)+(η3-η4)=2(η1+2η2+2η3+η4)-3(η1+η2+η3+η4)=(0,60,0,-96,-24)T
ξ2=(η1-η3)+(η2-η4)=2(2η1+2η2+η3+η4)-3(η1+η2+η3+η4)=(24,-36,-36,24,24)T
ξ1,ξ2是导出组的两个线性无关的解向量。又有
A[(η1+η2+η3+η4)/4]=(Aη1+Aη2+Aη3+Aη4)/4=(1/4)·4b=b所以η*=(η1+η2+η3+η4)/4=(1,-2,-3,3,4)T是AX=b的特解。故AX=b的通解为η=η*+k1ξ1+k2ξ2,k1,k2为任意常数。解析： 暂无解析 -
第13题：
画出函数 y=x²-2x-3的图象，利用图象回答：
（1）方程 x²-2x-3=0 的解是什么；
（2）x取什么值时，函数值大于0 ；
（3）x取什么值时，函数值小于0 。
-
第14题：
设A=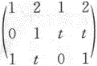
,且AX=0的基础解系含有两个线性无关的解向量,求AX=0的通解.答案：解析：
-
第15题：
设随机变量X~U（0，1)，Y~E（1），且X,Y相互独立，求Z=X+Y的密度函数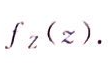
答案：解析：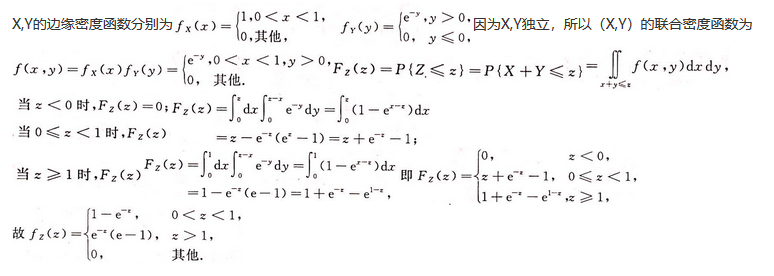
-
第16题：
设X,Y相互独立,且X～B
,Y～N(0,1),令U=max{X,Y},求P{1答案：解析：【解】P(U≤u)=P(max{X，Y}≤u)=P(X≤u，Y≤u)=P(X≤u)P(Y≤u)，
P(U≤1.96)=P(X≤1.96)P(Y≤1.96)=［P(X=0)+P(X=1)］P(Y≤1.96)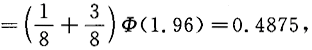
P(U≤1)=P(X≤1)P(Y≤1)=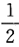
×Ф(1)=0.4205，
则P(1小于U≤1.96)=P(U≤1.96)-P(U≤1)=0.067.第17题：
设n元线性方程组Ax=b，其中
.
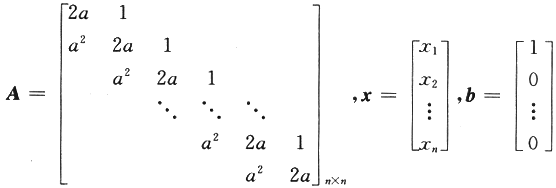
(Ⅰ)证明行列式｜A｜=(n+1)a^n；
(Ⅱ)当a为何值时，该方程组有唯一解，并求x1；
(Ⅲ)当a为何值时，该方程组有无穷多解，并求通解.答案：解析：
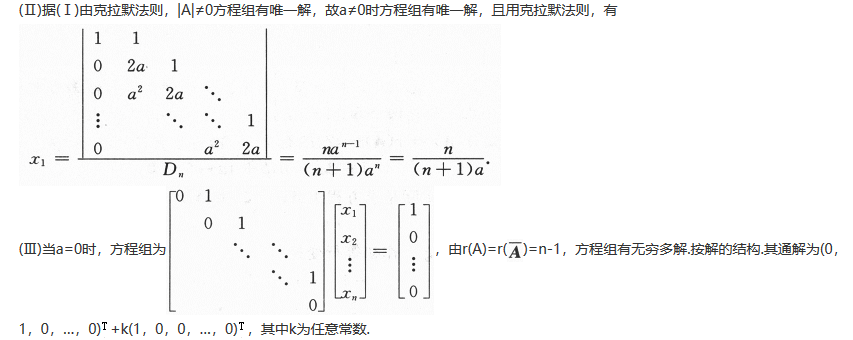
第18题：
设线性方程组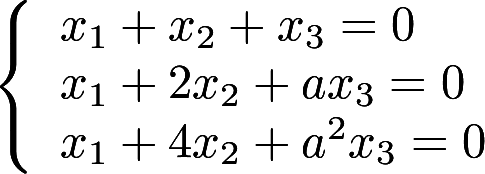
与方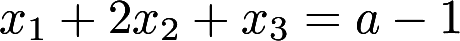
程有公共解，求a的值及所有公共解答案：解析：
第19题：
设线性方程组(I)与(II)有公共的非零解,其中(I)为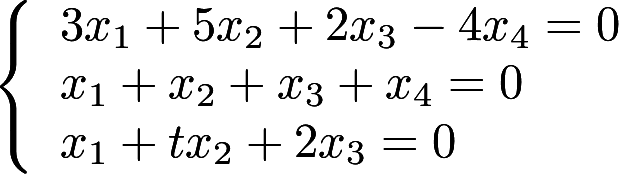
，(II)有基础解系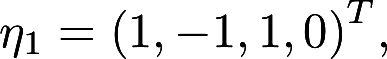
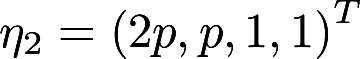，求p,t的值和全部公共解答案：解析：
第20题：
设矩阵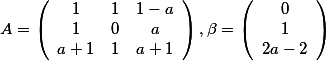
且方程组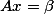
无解， （Ⅰ）求a的值； （Ⅱ） 求方程组
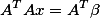的通解答案：解析：
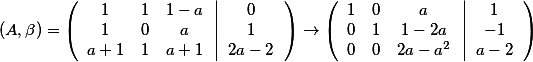当a=0时，
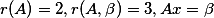无解第21题：
一平面简谐波沿X轴正向传播，已知x=1（1<λ）处质点的振动方程为y=Acoswt+φ0），波速为u，那么x=0处质点的振动方程为：（）
- A、y=Acos［w（t+1/u）+φ0］
- B、y=ACOS［w（t-1/u）+φ0］
- C、y=Acos［wt+1/u+φ0］
- D、y=Acos［wt-1/u+φ0］
正确答案:A第22题：
电容器的电流i＝C•du／dt，当u＞0，du／dt＞0时，则表明电容器正在（）。
- A、放电；
- B、充电；
- C、反方向充电；
- D、反方向放电。
正确答案:B第23题：
问答题编程实现用Euler法求初值问题的数值解，设方程如下：du/dt=√u+5u，且u（0）=1，t=[0，10]，并取步长h=0.1。正确答案： t=0:0.1:10;
n=length(t);
h=0.1;
u(1)=1;
uu=1;
for i=2:n
du=(sqrt(uu)+5*uu)*h;
uu=uu+du;
u(i)=uu;
end解析： 暂无解析