itgle.com
已知圆内接四边形ABCD中，AB、CD的延长线交与点F，则F=（）A、40°B、50°C、60°D、70°
题目
已知圆内接四边形ABCD中，AB、CD的延长线交与点F，则F=（）
- A、40°
- B、50°
- C、60°
- D、70°
相似考题
更多“已知圆内接四边形ABCD中，AB、CD的延长线交与点F，则F=（）A、40°B、50°C、60°D、70°”相关问题
-
第1题：
对边相等,对角相等的凸四边形,是平行四边形吧?方法①∠B小于90°；
左上为A，左下为B，右下为C，右上为D；
已知∠B=∠D；AB=CD;
证明：过A作AN⊥BC于N；
过C作CM⊥AD于M；
连接AC
∵AN⊥BC；CM⊥AD
∴∠ANB=∠DMC=90°
又∵∠B=∠D；AB=CD
∴△ANB=△DMC(AAS）
∴AN=CM;BN=DM
又∵∠ANB=∠DMC=90°，AC=AC
∴△ACD=△AMD（HL）
∴AM=DN
又∵BN=DM
∴BD=AC
∵BD=AC；AB=CD
∴凸四边形ABCD为平行四边型。
方法②∠B大于90°
左上为A，左下为B，右下为C，右上为D；
已知∠B=∠D；AB=CD;
证明：延长CD,过A作AN⊥BC于N；
延长AB,过C作CM⊥AD于M；
连接AC
∵AN⊥BC；CM⊥AD
∴∠ANB=∠DMC=90°
又∵∠B=∠D；AB=CD
∴△ANB=△DMC(AAS）
∴AN=CM;BN=DM
又∵∠ANB=∠DMC=90°，AC=AC
∴△ACD=△AMD（HL）
∴AM=DN
又∵BN=DM
∴BD=AC
∵BD=AC；AB=CD
∴凸四边形ABCD为平行四边型。
方法③∠B等于90°
证明：∵∠B=∠D=90°；AB=CD；AC=AC
∴△ABC=△ADC（HL）
∴AB=CB
∵BD=AC；AB=CD
∴凸四边形ABCD为平行四边型。
有错吗？若我的证明有错请明示，我知道有个反例，但它是凹四边形。
是平行四边形 -
第2题：
如图，四边形ABCD中，AB=10，AD=m，∠D=60o，以AB为直径作⊙O。
(1)求圆心0到CD的距离(用含m的代数式表示)；
(2)当m取何值时，CD与⊙0相切?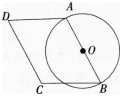
答案：解析：
-
第3题：
如图，四边形ABCD与四边形DEFG都是矩形，顶点F在BA的延长线上，边DG与AF交于点H，AD=4，DH=5，EF=6，求FG的长.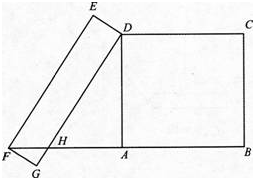
答案：解析：解：∵四边形ABCD和四边形DEFG均为矩形，
∴∠DAF=∠DAB=90°，∠G=90°，DG=EF.
∵EF=6，DH=5，∴GH=DG-DH=EF-DH=6-5=1
在Rt△ADH中，AD=4，DH=5，
-
第4题：
在平行四边形ABCD中，∠DAB=60，AB=15cm，已知圆O的半径等于3cm，AB，AD分别与圆O相切于点E，F.圆0在平行四边形ABCD内沿AB方向滚动，与BC边相切时运动停止．试求圆O滚过的路程．答案：解析：
-
第5题：
如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD2+CD2=2AB2.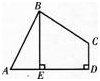
(1)求证：AB=BC；
(2)当BE⊥AD于E时，试证明：BE=AE+CD.答案：解析：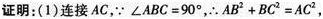
-
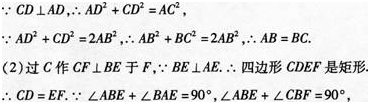
第6题：
如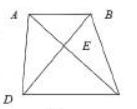
，在四边形ABCD中，AB//CD，AB与CD的边长分别为4和8，若ABE的面积为4，则四边形ABCD的面积为（ ）A.24
B.30
C.32
D.36
E.40答案：D解析： -
第7题：
如图8，四边形ABCD内接于⊙O，若∠BCD=130o，则∠BOD=_______°。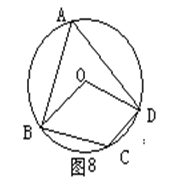
答案：解析：100 -
第8题：
圆内接四边形ABCD的一组对边AD、BC的延长线相交于户，对角线AC、BD相交于Q点，则图中共有相似三角形（）。
- A、4对
- B、2对
- C、1对
- D、3对
正确答案:A -
第9题：
设有关系模式R（A，B，C，D），F是R上成立的FD集，F＝{AB→C，D→A}，则属性集（CD）的闭包（CD）+为（）
- A、CD
- B、ACD
- C、BCD
- D、ABCD
正确答案:B -
第10题：
设关系模式R（ABCD），F是R上成立的FD集，F={AB→CD，A→D}。试把R分解成2NF模式集。
正确答案:如果将R分解成{AD，ABC}，则是2NF模式集。 -
第11题：
单选题圆内接四边形ABCD中，已知∠A＝70°，则∠C＝（ ）．A20°
B30°
C70°
D110°
正确答案： D解析：
圆内接四边形的对角互补，所以∠C＝110°． -
第12题：
单选题已知圆内接四边形ABCD中，AB、CD的延长线交与点F，则F=（）A40°
B50°
C60°
D70°
正确答案： B解析： 暂无解析 -
第13题：
设关系模式R (U，F)，其中U为属性集， F是U上的一组函数依赖，那么函数依赖的公理系统（Armstrong公理系统）中的合并规则是指为（ ）为F所蕴涵。
A.若A→B，B→C，则A→CB.若Y⊆X⊆U，则X→Y。C.若A→B，A→C ,则A→BCD.若A→B，C⊆B,则A→C
正确答案：C
-
第14题：
如图。在直角梯形ABCD中，AB∥CD，∠BAD=90o，且AB=8，AD=3，CD=4，动点P，Q分别以点B和点A为起点同时出发，点P沿B→A，以每秒1个单位速度运动，终点为点A；点Q沿A→D→C→B，以每秒1.5个单位速度运动，终点为点B。设△APQ的面积为y，运动时间为x。
(1)求y关于x的函数解析式y=f(x)；
(2)画出函数y=f(x)的图象。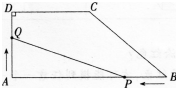
答案：解析：
(2)函数图象如图所示：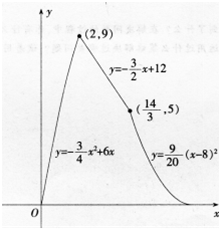
-
第15题：
如下图，平行四边形ABCD的对角线相交于点O，直线EF经过点O，分别与AB，CD的延长线交于点E，F．求证：四边形AECF是平行四边形．
答案：解析：证明：如右图所示，∵四边形ABCD为平行四边形，∴BO=DO，
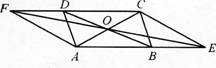
又∵AB∥CD，∴∠FDO=∠EB0
-
第16题：
如图,D是△ABC内的一点，BD⊥CD，AD=6，BD=8，CD=6，E，F，G，H分别是AB，AC，CD， BD的中点．则四边形EFGH的周长是()。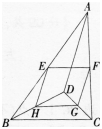
A.12
B.14
C.15
D.16答案：D解析：因为BD⊥CD，BD=8，CD=6，由勾股定理可知BC=10。由三角形中位线定理可知EH=FG=
-
第17题：
如图，平面四边形ABCD中，AB=2，BC=4，CD=5，DA=3，
(1)若∠B与∠D互补，求AC2的值；
(2)求平面四边形ABCD面积的最大值。
答案：解析：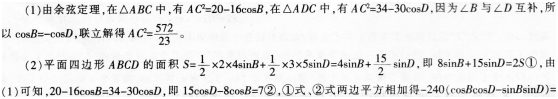
-
第18题：
平行四边形ABCD如右图所示，E为AB上的一点，F、G分别是AC和DE、DB的交点。若AB=3AE，则四边形BEFG与ABCD的面积之比是：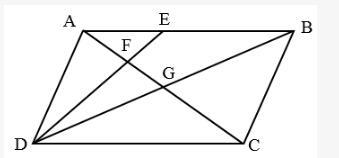
A.2︰7
B.3︰13
C.4︰19
D.5︰24答案：D解析：第一步，本题考查几何问题，属于平面几何类，用赋值法解题。
第二步，题干没给出具体数值，可以采用赋值法解题。赋值AB=3，平行四边形ABCD的高为4，则AE=1；由于△AEF相似于△CDF，则两个三角形的高之比为AE：DC=1︰3，可知△AEF的高为4×1/4=1。△ABG与△CDG全等，则△ABG的高为4÷2=2。
第三步，四边形BEFG面积=△ABG面积-△AEF面积=
四边形ABCD面积=3×4=12，两者之比为5/2 ︰12=5︰24。
因此，选择D选项。 -
第19题：
如图，平行四边形ABCD的面积是54平方厘米，点E、F、G分别是平行四边形ABCD边上的中点，H为AD边上的任意一点，则阴影部分的面积为（ ）平方厘米。
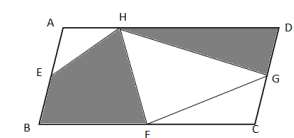A. 27
B. 28
C. 32
D. 36答案：A解析：方法一：如图所示，由于H为AD边上的任意一点，假设H点与A点重叠，则左边阴影为三角形ABF，其面积为三角形ABC的一半；右边阴影为三角形ADG，其面积为三角形ACD的一半。因此题目所求为平行四边形ABCD面积的一半，平行四边形ABCD的面积是54平方厘米，则阴影部分面积为27平方厘米。因此，本题答案为A选项。
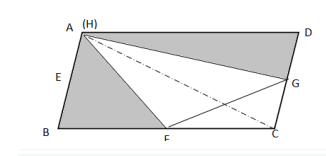
方法二：如图所示，连接BH和CH，由于点E、F、G分别是平行四边形ABCD边上的中点，则三角形AEH和BEH相等，三角形BFH和CFH相等，三角形CGH和DGH相等，因此题目所求的阴影部分为平行四边形ABCD的一半。平行四边形ABCD的面积是54平方厘米，则阴影部分面积为27平方厘米。因此，本题答案为A选项。
-
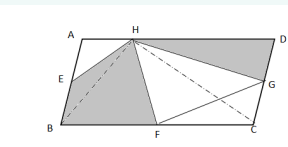
第20题：
逻辑代数式子f=AB+ABC+AB（C+D），则f的简化式子为（）。
- A、AB
- B、A+B
- C、ABC
- D、ABCD
正确答案:A -
第21题：
设关系模式R（ABCD），F是R上成立的FD集，F={AB→CD，A→D}。试说明R不是2NF模式的理由。
正确答案:从已知的函数依赖集F，可知R的候选键是AB。另外，由AB→CD可推出AB→D，再由A→D可知AB→D是部分（局部）函数依赖，因此R不是2NF模式。 -
第22题：
在曲柄摇杆机构中，已知连杆BC=50mm、摇杆CD=40mm、机架AD=40mm，则曲柄AB的取值范围是（）。
正确答案:0＜AB≤30mm -
第23题：
单选题圆内接四边形ABCD的一组对边AD、BC的延长线相交于户，对角线AC、BD相交于Q点，则图中共有相似三角形（）。A4对
B2对
C1对
D3对
正确答案： A解析： 暂无解析