举例说明高中数学内容在现实生活中的原型。
题目
举例说明高中数学内容在现实生活中的原型。
相似考题
更多“举例说明高中数学内容在现实生活中的原型。”相关问题
-
第1题:
数学应用是贯穿高中数学课程的一条主线,其应用主线结构图如下图所示: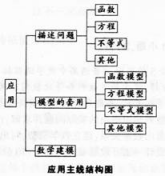
20世纪中叶以来,由于计算机和现代信息技术的飞速发展,使应用数学和数学应用得到了前所未有的发展,数学渗透到几乎每一个学科领域和人们日常生活的每一个角落。数学应用的巨大发展成为数学发展的显著特征之一。
(1)请举例说明高中数学内容在现实生活中的原型。
(2)分析高中数学教学中存在的问题。答案:解析:(1)函数有丰富的实际背景,出租车的计价、邮局寄包裹的计费都是分段函数的实际应用:考古学中也应用到了指数函数的性质;简谐振动的数学模型就是三角函数;平抛运动抽象为数学模型就是二次函数。
又例如:储蓄中的单利问题是等差数列模型,复利问题是等比数列模型。
算法中的取最小值问题、排序问题都是实际中常见的。
生活中的掷硬币决胜负、抽签决定出场次序都是概率模型在生活中的应用。
在研究力和速度时,向量就是很好的模型。
宇宙天体的运行轨道、铅球出手后的运动轨迹、汽车的广角灯等,都是圆锥曲线模型在实际中的应用。
通过这些实际例子,可以帮助我们更深刻地理解数学中的重要概念,有了对于这些重要概念(模型)的本质理解,就可以更好地利用这些模型来刻画(描述)实际问题。
(2)在我国数学教学中,比较突出的一个问题是忽视数学的应用,忽视数学与其他学科以及与日常生活的联系,忽视培养学生的应用意识。在很长一段时期内,数学教育界过分强调“数学是思维的体操”。把数学应用斥之为“实用主义”“短视行为”。1995年以后,虽然数学应用的呼声渐高,但是数学课程中对数学应用的重视程度还是比较低的。由于数学课程与教学中对数学应用的忽视,使学生在数学学习中,不能足够地认识到数学的应用价值、数学与日常生活以及其他学科的联系。 -
第2题:

20世纪中叶以来,由于计算机和现代信息技术的飞速发展,使应用数学和数学应用得到了前所未有的发展,数学渗透到几乎每一个学科领域和人们日常生活的每一个角落。数学应用的巨大发展成为数学发展的显著特征之一。
(1)请举例说明高中数学内容在现实生活中的原型。
(2)分析高中数学教学中存在的问题。答案:解析:(1)函数有丰富的实际背景,出租车的计价、邮局寄包裹的计费都是分段函数的实际应用:考古学中也应用到了指数函数的性质;简谐振动的数学模型就是三角函数;平抛运动抽象为数学模型就是二次函数。
又例如:储蓄中的单利问题是等差数列模型,复利问题是等比数列模型。
算法中的取最小值问题、排序问题都是实际中常见的。
生活中的掷硬币决胜负、抽签决定出场次序都是概率模型在生活中的应用。
在研究力和速度时,向量就是很好的模型。
宇宙天体的运行轨道、铅球出手后的运动轨迹、汽车的广角灯等,都是圆锥曲线模型在实际中的应用。
通过这些实际例子,可以帮助我们更深刻地理解数学中的重要概念,有了对于这些重要概念(模型)的本质理解,就可以更好地利用这些模型来刻画(描述)实际问题。
(2)在我国数学教学中,比较突出的一个问题是忽视数学的应用,忽视数学与其他学科以及与日常生活的联系,忽视培养学生的应用意识。在很长一段时期内,数学教育界过分强调“数学是思维的体操”。把数学应用斥之为“实用主义”“短视行为”。1995年以后,虽然数学应用的呼声渐高,但是数学课程中对数学应用的重视程度还是比较低的。由于数学课程与教学中对数学应用的忽视,使学生在数学学习中,不能足够地认识到数学的应用价值、数学与日常生活以及其他学科的联系。 -
第3题:
在现实生活中,你经历过哪些变苦、苦苦、行苦?请举例说明。
正确答案: 变苦:如得得一些爱不释手的东西,却一不小心给打碎了。亲友难得相聚,却很快就分离了...
苦苦:记得刚走上社会不久,单位体验时发现很一些病患,心里瞬间痛苦不已,而此时平时要好的同事也纷纷躲避,没过几日工作也失去了。
平时吃饭穿衣、住房受用、装饰设宴等,无不隐藏着痛苦,有漏法不离迁流变化,这就是行苦。 -
第4题:
举例说明在高中数学课程中,如何利用整体性质讨论方程的近似解。
正确答案: 首先举一个利用二分法判断方程根的存在性的实例。
例如判断方程x2-x-6=0的根的存在性。我们可以考查函数f(x)=x2-x-6,图象为抛物线。易得f(0)=-6<0,f(4)=6>0,f(-4)=14>0。
由于函数f(x)的图象是连续曲线,因此点B(0,-6)与点C(4,6)之间的那部分曲线必然穿过x轴,即在区间(0,4)内必有一点x1,使f(x1)=0;同样,在区间(-4,0)内也必有一点x2,使f(x2)=0。所以方程x2-x-6=0有两个实根。
二分法本质上就是用函数的整体性质“函数在闭区间连续,且端点函数值异号”,去寻求函数图象与x轴的交点。除了二分法外,在数学分析中,还有一些用整体性质讨论方程近似解的方法,这些方法都是从整体看待局部。例如切线法,如果一个函数y=f(x)在闲区间有一阶导数,则可用切线法求方程f(x)=0的解。再例如,割线法,如果一个函数y=f(x)在闭区间有二阶导数,则可用割线法求方程y=f(x)的解。在“计算方法”中可以证明:切线法比二分法快,割线法比切线法快。这是因为,割线法比切线法要求函数具有更好的性质,切线法比二分法要求函数具有更好的性质。 -
第5题:
举例说明“度”这一范畴在现实生活的意义。
正确答案:事物的度是事物的质和量的统一,度是事物保持其质的数量界限,它表示事物的质所依赖的数量的变化幅度和范围。度的两端称为“关节点”或“临界点”。事物的数量变化超出这个“关节点”事物的质就会改变,水在加热过程中,只要尚未达到“沸点”它就处于量变过程,加热超过100`C,它就会变成汽,就会发生质变,100度就是水的临点,超过这个温度,水就发生了质变。凡一切事物皆有一定的尺度,追求财富、荣誉、权力等并不是坏事,但是不顾一切地去追求这些东西,甚至为这些东西而违法犯罪,就会事与愿违,走向事物的反面,将好事变成坏事。“乐极生悲”也是这个道理。 -
第6题:
在高中数学课程中为什么要讲微积分初步?
正确答案:(1)微积分的思想是非常重要的思想,它可以帮助我们了解函数的变化,刻画现实世界中的规律。在日常生活中,微积分的基本知识已经成为人们认识某些事物的常识。很多中学生中学毕业之后会直接进入工作岗位,希望学生通过微积分的学习,能用变化和运动的观点来看待数学世界和现实世界,能有一个更加广阔的数学视野。
(2)在中学阶段所学到的相关的学科,比如物理、化学、生物、地理等,都有很多反映微积分思想的实例和案例,所以在数学上给出微积分的表述,对于理解这些事例和案例是必要的。
(3)直接介绍微积分的难度不大,能为中学生所接受。
(4)可以帮助学生了解导数和积分的丰富背景和应用,建立一些具体的、特殊的极限概念,初步形成对极限的感性认识,这些对于进一步学习微积分理论是有帮助的。(5)微积分的产生在人类文明史上有着重要的作用。通过这部分内容的学习可以让学生更好地理解数学在人类进步和发展中不可缺少的作用。 -
第7题:
《林海雪原》以现实生活中的真人真事为原型,塑造了()这一英雄形象。这部小说在艺术上具有突出的浪漫主义传奇色彩。
正确答案:杨子荣 -
第8题:
问答题举例说明原型意象和抒情母题的关系。正确答案: 如自古代有折柳送别的习俗,而且“柳与留”谐音,这都暗示柳树与离别情绪之间存在某种联系,为使柳树成为表达离别情绪这一母题的原型意象奠定了基础。解析: 暂无解析 -
第9题:
问答题举例说明“度”这一范畴在现实生活的意义。正确答案: 事物的度是事物的质和量的统一,度是事物保持其质的数量界限,它表示事物的质所依赖的数量的变化幅度和范围。度的两端称为“关节点”或“临界点”。事物的数量变化超出这个“关节点”事物的质就会改变,水在加热过程中,只要尚未达到“沸点”它就处于量变过程,加热超过100`C,它就会变成汽,就会发生质变,100度就是水的临点,超过这个温度,水就发生了质变。凡一切事物皆有一定的尺度,追求财富、荣誉、权力等并不是坏事,但是不顾一切地去追求这些东西,甚至为这些东西而违法犯罪,就会事与愿违,走向事物的反面,将好事变成坏事。“乐极生悲”也是这个道理。解析: 暂无解析 -
第10题:
问答题举例说明在高中数学课程中,如何利用整体性质讨论方程的近似解。正确答案: 首先举一个利用二分法判断方程根的存在性的实例。
例如判断方程x2-x-6=0的根的存在性。我们可以考查函数f(x)=x2-x-6,图象为抛物线。易得f(0)=-6<0,f(4)=6>0,f(-4)=14>0。
由于函数f(x)的图象是连续曲线,因此点B(0,-6)与点C(4,6)之间的那部分曲线必然穿过x轴,即在区间(0,4)内必有一点x1,使f(x1)=0;同样,在区间(-4,0)内也必有一点x2,使f(x2)=0。所以方程x2-x-6=0有两个实根。
二分法本质上就是用函数的整体性质“函数在闭区间连续,且端点函数值异号”,去寻求函数图象与x轴的交点。除了二分法外,在数学分析中,还有一些用整体性质讨论方程近似解的方法,这些方法都是从整体看待局部。例如切线法,如果一个函数y=f(x)在闲区间有一阶导数,则可用切线法求方程f(x)=0的解。再例如,割线法,如果一个函数y=f(x)在闭区间有二阶导数,则可用割线法求方程y=f(x)的解。在“计算方法”中可以证明:切线法比二分法快,割线法比切线法快。这是因为,割线法比切线法要求函数具有更好的性质,切线法比二分法要求函数具有更好的性质。解析: 暂无解析 -
第11题:
问答题举例说明高中数学内容在现实生活中的原型。正确答案: 函数有丰富的实际背景,出租车的计价、邮局寄包裹的计费都是分段函数的实际应用;考古学中也应用到了指数函数的性质;简谐振动的数学模型就是三角函数;平抛运动抽象为数学模型就是二次函数。又例如:储蓄中的单利问题是等差数列模型,复利问题是等比数列模型。算法中的取最小值问题、排序问题都是实际中常见的。生活中的掷硬币决胜负、抽签决定出场次序都是概率模型在生活申的应用。在研究力和速度时,向量就是很好的模型。宇宙天体的运行轨道、铅球出手后的运动轨迹、汽车的广角灯等,都是圆锥曲线模型在实际中的应用。通过这些实际例子,可以帮助我们更深刻地理解数学中的重要概念,有了对于这些重要概念(模型)的本质理解,就可以更好地利用这些模型采刻画(描述)实际问题。解析: 暂无解析 -
第12题:
问答题在现实生活中,你经历过哪些变苦、苦苦、行苦?请举例说明。正确答案: 变苦:如得得一些爱不释手的东西,却一不小心给打碎了。亲友难得相聚,却很快就分离了...
苦苦:记得刚走上社会不久,单位体验时发现很一些病患,心里瞬间痛苦不已,而此时平时要好的同事也纷纷躲避,没过几日工作也失去了。
平时吃饭穿衣、住房受用、装饰设宴等,无不隐藏着痛苦,有漏法不离迁流变化,这就是行苦。解析: 暂无解析 -
第13题:
简述《普通高中数学课程标准(实验)》中必修课程内容确定的原则和选修课程内容确定的原则。答案:解析:必修课程内容确定的原则是:满足未来公民的基本数学需求,为学生进一步的学习提供必要 的数学准备。
选修课程内容确定的原则是:满足学生的兴趣和对未来发展的需求,为学生进一步学习、获得较高数学素 养奠定基础。其中,系列1是为那些希望在人文、社会科学等方面发展的学生而设置的,系列2则是为那些希望 在理工、经济等方面发展的学生而设置的。系列1、系列2内容是选修系列课程中的基础性内容。系列3和系列4是为对数学有兴趣和希望进一步提高数学素养的学生而设置的,所涉及的内容反映了某些重要的数学思想, 有助于学生进一步打好数学基础,提高应用意识,有利于学生终身的发展,有利于扩展学生的数学视野,有利于 提高学生对数学的科学价值、应用价值、文化价值的认识。 -
第14题:
下列关于高中数学课程的变化内容,说法不正确的是( )A.高中数学课程中的向量既是几何的研究对象,也是代数的研究对象
B.高中数学课程中,概率的学习重点是如何计数
C.算法是培养逻辑推理能力的非常好的载体
D.集合论是一个重要的数学分支答案:C解析:高中数学课程中向量既是几何的研究对象,也是代数的研究对象,向量是沟通几何与代数的一座天然桥梁;算法是培养逻辑推理能力的非常好的载体,在大学和中学数学教育中都发挥着重要的作用;集合论是一个重要的数学分支,教师要准确把握高中数学课程中集合这一内容的定位;在概率课中,学习的重点是如何理解随机现象而不是如何计数。 -
第15题:
下列关于高中数学课程的变化内容,说法不正确的是()。
- A、高中数学课程中的向量既是几何的研究对象,也是代数的研究对象
- B、高中数学课程中,概率的学习重点是如何计数
- C、算法是培养逻辑推理能力的非常好的载体
- D、集合论是一个重要的数学分支
正确答案:B -
第16题:
在现实生活中,“看不见的手”能否在所有领域发挥作用?请举例说明。
正确答案:看不见的手是依靠市场去自行调控,通过供需来控制,但是市场经济往往具有一定的盲目性,例如看见养猪挣钱,结果许多人扎堆去养猪,结果导致供过于求,造成产能过剩,浪费等不经济的现象。
看得见的手是指政府的宏观调控,例如淘汰落后产业等等,一定程度上促进了效率。但不能过度干预,否则就会形成像计划经济了。 -
第17题:
举例说明快速原型制造技术通常应用的场合。
正确答案: (1)新产品开发
(2)原型制造
(3)模具制造
(4)零部件制造及其他领域的应用 -
第18题:
什么是原型启发?它在创造发明或思维中有何作用?举例说明。
正确答案:原型启发是从其它事物中看出解决问题的途径和方法。对思维具有启发作用的事物叫做原型;任何事物、现象和活动都可以成为原型。
原型在创造发明或思维中既可起到积极作用,也可以起消极作用。
例如:鲁班根据丝茅草划破手指发明了锯,丝茅草是原型,发明锯就是受原型启发。 -
第19题:
举例说明原型意象和抒情母题的关系。
正确答案:如自古代有折柳送别的习俗,而且“柳与留”谐音,这都暗示柳树与离别情绪之间存在某种联系,为使柳树成为表达离别情绪这一母题的原型意象奠定了基础。 -
第20题:
单选题从现实生活的事例中受到启发而找到解决问题的途径和方法叫()。A技能学习
B原型启发
C灵感
D顿悟
正确答案: D解析: 暂无解析 -
第21题:
填空题数学探究、()、数学文化是贯彻于整个高中数学课程的重要内容,这些内容不单独设置,渗透在每个模块或专题中。正确答案: 数学建模解析: 暂无解析 -
第22题:
填空题《林海雪原》以现实生活中的真人真事为原型,塑造了()这一英雄形象。这部小说在艺术上具有突出的浪漫主义传奇色彩。正确答案: 杨子荣解析: 暂无解析 -
第23题:
问答题表面为什么具有吸附作用?物理吸附和化学吸附的主要起源于什么?举例说明现实生活中的吸附粒子?正确答案: (1)吸附是指外来的原子或分子气体在界面上富集的现象。气体分子或原子分子咋表面吸附可以不同程度上抵消表面原子的不平衡力场,使作用力的分布趋于对称,于是就降低了表面能,使体系处于较低的能量状态,体系更为稳定,所以吸附过程是自发进行的。
(2)物理吸附源自于范德华耳斯力作用而相互吸引,物理吸附无选择性;化学吸附则源自于剩余的不饱和键力,化学吸附有选择性。解析: 暂无解析
