itgle.com
单选题变直径圆管流，细断面直径d1，粗断面直径d2=2d1，粗细断面雷诺数的关系是（ ）。A <p>Re<sub>1</sub>=0.5Re<sub>2</sub></p>B <p>Re<sub>1</sub>=Re<sub>2</sub></p>C <p>Re<sub>1</sub>=1.5Re<sub>2</sub></p>D <p>Re<sub>1</sub>=2Re<sub>2</sub> </p>
题目
<p>Re<sub>1</sub>=0.5Re<sub>2</sub></p>
<p>Re<sub>1</sub>=Re<sub>2</sub></p>
<p>Re<sub>1</sub>=1.5Re<sub>2</sub></p>
<p>Re<sub>1</sub>=2Re<sub>2</sub> </p>
相似考题
更多“变直径圆管流，细断面直径d1，粗断面直径d2=2d1，粗细断面雷诺数的关系是（ ）。”相关问题
-
第1题：
变直径圆管流，细断面直径d1，粗断面直径d2=2d1，粗细断面雷诺数的关系是:
A. Re1=0. 5Re2 C. Re1 =1. 5Re2
B. Re1=Re2 D. Re1 =2Re2答案：D解析：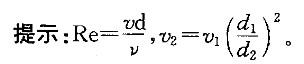
-
第2题：
变直径有压圆管内的流动，上游断面1的直径d1=150mm，下游断面2的直径d2=300mm。断面1的平均流速v1，断面2的平均流速v2为：
A. 3m/s B. 2m/s C. 1.5m/s D.1m/s答案：C解析：提示:应用连续方程v2=v1A1/A2。 -
第3题：
变直径圆管，前段直径d1=30mm，雷诺数为3000，后段直径变为d2=60mm，则后段圆管的雷诺数为（ ）。
A． 1000
B． 1500
C． 2000
D． 3000答案：B解析：雷诺数是流体流动的关键参数，要求会计算。由连续性方程A1V1=A2V2，可得：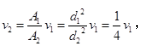
-
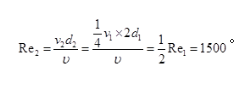
第4题：
变直径圆管流，细断面直径d1，粗断面直径d2=2d1，粗细断面雷诺数的关系是:A. Re1=0. 5Re2
B. Re1 =1. 5Re2
C. Re1=Re2
D. Re1 =2Re2答案：D解析：
-
第5题：
变直径管流，细断面直径D1，粗断面直径D2=2D1，粗细断面雷诺数的关系是：（）
ARe1=0.5Re2；
BRe1=Re2；
CRe1=1.5Re2；
DRe1=2Re2。
D
略 -
第6题：
变直径圆管流，细断面直径d1，粗断面直径d2=2d1，粗细断面雷诺数的关系是：（）
- A、Re1=0.5Re2
- B、Re1=Re2
- C、Re1=1.5Re2
- D、Re1=2Re2
正确答案:D -
第7题：
有压圆管恒定流，若断面1的直径是其下游断面2的直径的二倍，则断面1的雷诺数Re1与断面2的雷诺数Re2的关系是（）
- A、Re1=Re2
- B、Re1=0.5Re2
- C、Re1=1.5Re2
- D、Re1=2Re2
正确答案:B -
第8题：
变直径管流，细断面直径为d1=30mm，雷诺数为5000，粗断面直径d2=2d1，则粗断面管中雷诺数是（）。
- A、5000
- B、4000
- C、2500
- D、1250
正确答案:C -
第9题：
问答题有一直径缓慢变化的锥形水管，断面1处直径d1=0.15m，断面2处直径d2=0.3m，断面2处流速v2为1.5m/s，试求断面1处的流速？正确答案： 根据连续方程，v1×A1=v2×A2
故v1=（A2/A1）×v2=（πd22/4）v2/（πd12/4）=（d2/d1）2v2=（0.30/0.15）2×1.5=6m/s。解析： 暂无解析 -
第10题：
单选题变直径圆管流，细断面直径d1，粗断面直径d2=2d1，粗细断面雷诺数的关系是（ ）。ARe1=0.5Re2
BRe1=Re2
CRe1=1.5Re2
DRe1=2Re2
正确答案： B解析：
同一总流上，各断面平均流速v与断面面积成反比，故v1=4v2，雷诺数Re=vd/ν，对特定流体，ν一定，从而与vd成正比，故Re1/Re2=（v1d1）/（v2d2）=（4v2d1）/（2v2d1）=2。 -
第11题：
单选题有压圆管恒定流，若断面1的直径是其下游断面2直径的两倍，则断面1的雷诺数Rei与断面2的雷诺数Re2的关系是：（）ARe1=Re2
BRe1=0.5Re2
CRe1=1.5Re2
DRe1=2Re2
正确答案： B解析： 暂无解析 -
第12题：
单选题变直径管流，细断面直径D1，粗断面直径D2=2D1，粗细断面雷诺数的关系是：（）ARe1=0.5Re2；
BRe1=Re2；
CRe1=1.5Re2；
DRe1=2Re2。
正确答案： D解析： 暂无解析 -
第13题：
有压圆管恒定流，若断面1的直径是其下游断面2直径的两倍，则断面1的雷诺数Re1与断面2的雷诺数Re2的关系是：
A. Re1=0. 5Re2 C. Re1 =1. 5Re2
B. Re1=Re2 D. Re1 =2Re2答案：B解析：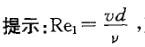
直径减小一半，流速增加4倍。Re随d减少而增加。 -
第14题：
变直径有压圆管的流动，上游断面1的直径d1＝150mm，下游断面2的直径d2＝300mm，断面1的平均流速v1＝6m/s，断面2的平均流速v2为（ ）m/s。A．1
B．1.5
C．2
D．3答案：B解析：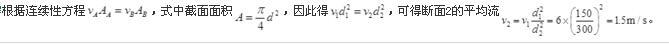
-
第15题：
有压圆管恒定流，若断面1的直径是其下游断面2直径的两倍，则断面1的雷诺数Re1与断面2的雷诺数Re2的关系是：A. Re1=0. 5Re2
B. Re1 =1. 5Re2
C. Re1=Re2
D. Re1 =2Re2答案：B解析：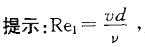
直径减小一半，流速增加4倍。Re随d减少而增加。 -
第16题：
变直径管流细断面直径为d1，粗断面直径d2＝2d1，粗细断面雷诺系数的关系是（ ）。A．Re1＝0.5Re2
B．Re1＝Re2
C．Re1＝1.5Re2
D．Re1＝2Re2答案：D解析：用圆管传输流体计算雷诺数时，定型尺寸一般取管道直径（d），则雷诺数Re＝vdρ/μ，而v＝Q/A＝4Q/πd2，换算得：
又d2＝2d1，所以Re1＝2Re2。 -
第17题：
有一直径缓慢变化的锥形水管，流量Q=4L/s，断面1处直径d1=0.05m，断面2处直径d2=0.1m，试求断面1、2处的平均流速？
正确答案: 根据连续方程，Q=v1×A1=v2×A2
故v1=Q/A1=Q/（πd12/4）=0.004/（3.14×0.05×0.05/4）=2.04m/s。
v2=Q/A2=Q/（πd22/4）=0.004/（3.14×0.1×0.1/4）=0.51m/s。 -
第18题：
有压圆管恒定流，若断面1的直径是其下游断面2直径的两倍，则断面1的雷诺数Rei与断面2的雷诺数Re2的关系是：（）
- A、Re1=Re2
- B、Re1=0.5Re2
- C、Re1=1.5Re2
- D、Re1=2Re2
正确答案:B -
第19题：
有一直径缓慢变化的锥形水管，断面1处直径d1=0.15m，断面2处直径d2=0.3m，断面2处流速v2为1.5m/s，试求断面1处的流速？
正确答案: 根据连续方程，v1×A1=v2×A2
故v1=（A2/A1）×v2=（πd22/4）v2/（πd12/4）=（d2/d1）2v2=（0.30/0.15）2×1.5=6m/s。 -
第20题：
单选题变直径圆管，前段直径d1＝30mm，雷诺数为3000，后段直径变为d2＝60mm，则后段圆管中的雷诺数为（ ）。[2012年真题]A1000
B1500
C2000
D3000
正确答案： A解析：
连续性方程的公式为：A1v1＝A2v2。由题意可得，d1/d2＝30/60＝1/2，则v2/v1＝A1/A2＝（d1/d2）2＝1/4。雷诺数Re＝vd/υ，则Re2/Re1＝（v2/v1）（d2/d1）＝（1/4）×2＝1/2。因此，后段圆管中的雷诺数Re2＝Re1/2＝3000/2＝1500。 -
第21题：
问答题有一直径缓慢变化的锥形水管，流量Q=4L/s，断面1处直径d1=0.05m，断面2处直径d2=0.1m，试求断面1、2处的平均流速？正确答案： 根据连续方程，Q=v1×A1=v2×A2
故v1=Q/A1=Q/（πd12/4）=0.004/（3.14×0.05×0.05/4）=2.04m/s。
v2=Q/A2=Q/（πd22/4）=0.004/（3.14×0.1×0.1/4）=0.51m/s。解析： 暂无解析 -
第22题：
单选题有压圆管恒定流，若断面1的直径是其下游断面2的直径的二倍，则断面1的雷诺数Re1与断面2的雷诺数Re2的关系是（）ARe1=Re2
BRe1=0.5Re2
CRe1=1.5Re2
DRe1=2Re2
正确答案： B解析： 暂无解析 -
第23题：
单选题水流经过变直径圆管，管中流量不变，已知前段直径d1＝30mm，雷诺数为5000，后段直径变为d2＝60mm，则后段圆管中的雷诺数为：（）A5000
B4000
C2500
D1250
正确答案： B解析： 暂无解析 -
第24题：
单选题变直径管流，细断面直径为d1，粗断面直径d2＝2d1，粗细面雷诺数的关系是（ ）。ARel＝0.5Re2
BRel＝Re2
CRel＝1.5Re2
DRel＝2Re2
正确答案： D解析：
根据连续性方程v1A1＝v2A2可知，v1＝v2A2/A1＝v2d22/d12＝4v2。因此，粗细雷诺数关系式为：Re1/Re2＝（v1d1/ν）/（v2d2/ν）＝（v1/v2）（d1/d2）＝4×0.5＝2，即Rel＝2Re2。