itgle.com

对同一目标进行三次独立射击，第一，二，三次射击的命中概率分别为0.4，0.5，0.7，试求 （1）在这三次射击中，恰好有一次击中目标的概率； （2）至少有一次命中目标的概率。

题目

对同一目标进行三次独立射击，第一，二，三次射击的命中概率分别为0.4，0.5，0.7，试求 （1）在这三次射击中，恰好有一次击中目标的概率； （2）至少有一次命中目标的概率。

相似考题

1.甲、乙两人独立的进行两次射击,每次射击甲命中概率为0.2,乙命中概率为0.5,X与Y分别表示甲、乙命中的次数,求X与Y的联合分布列。

2.甲、乙两人独立地向同一目标射击一次,其命中率分别为0.7和0.6,则目标被击中的概率是()。A.0.46B.1.8C.0.42D.0.88

3.某项飞碟射击比赛规定一个碟靶有两次命中机会(即允许在第一次脱靶后进行第二次射击)。某射击选手第一发命中的可能性是80%,第二发命中的可能性为50%。则该选手两发都脱靶的概率是()。A.0.9B.0.8C.0.1D.0.5

4.一射手对同一目标独立地进行四次射击,若至少命中一次的概率为80／81,则该射手的命中率为()A、1/3B、2/3C、1/6D、1/4

参考答案和解析
正确答案: P{三次射击恰击中目标一次}=0.4（1-0.5）（1-0.7）+（1-0.4）0.5（1-0.7）+（1-0.4）（1-0.5）0.7=0.36
P{至少有一次命中}=1-P{未击中一次}=1-（1-0.4）（1-0.5）（1-0.7）=0.91
更多“对同一目标进行三次独立射击，第一，二，三次射击的命中概率分别为”相关问题

  • 第1题：

    设一射手射击命中率稳定。射手对靶独立进行3次射击,一次也未命中的概率为1／27,则该射手射击的命中率为1／3。()

    此题为判断题(对，错)。


    正确答案：错误

  • 第2题：

    甲乙两人独立地向同一目标各射击一次，命中率分别为0.8和0.6，现已知目标被击中，则它是甲射中的概率为：

    A.0.26
    B.0.87
    C.0.52
    D.0.75

    答案：B
    解析：
    参考解析：提示：设“甲击中”为A，“乙击中”为B，A、B独立，目标被击中即甲、乙至少一人击中，求P(A│A+B)。


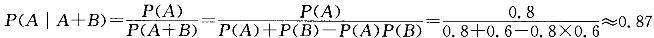
  • 第3题：

    甲、乙两人独立对同一目标进行射击,命中目标概率分别为60%和50%.
    　　(1)甲、乙两人同时向目标射击,求目标被命中的概率；
    　　(2)甲、乙两人任选一人,由此入射击,目标被击中,求是甲击中的概率.


    答案：
    解析：
    【解】(1)设A={甲击中目标}，B={乙击中目标}，C={击中目标}，则C=A+B，
    P(C)=P(A+B)=P(A)+P(B)-P(AB)=P(A)+P(B)-P(A)P(B)
    =0.6+0.5-0.6×0.5=0.8.
    (2)设A1={选中甲}，A2={选中乙}，B={目标被击中}，则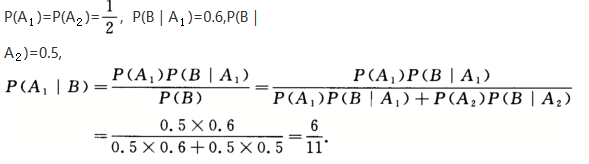

  • 第4题：

    已知军训打靶对目标进行 10 次独立射击，假设每次打靶射击命中率相同，若击中靶子次数的方差为 2.1，则每次命中靶子概率等于（ ）

    A.0.2
    B.0.3
    C.0.4
    D.0.5

    答案：B
    解析：

  • 第5题：

    甲，乙两人独立地对同一目标射击一次，其命中率分别为0.6和0.5，则目标被击中的概率为（）.

    • A、0.5
    • B、0.8
    • C、0.55
    • D、0.6

    正确答案:B

  • 第6题：

    已知一射手在两次独立射击中至少命中目标一次的概率为0.96，则该射手每次射击的命中率为（）

    • A、0.04
    • B、0.2
    • C、0.8
    • D、0.96

    正确答案:C

  • 第7题：

    对目标进行3次独立射击，每次射击的命中率相同，如果击中次数的方差为0.72，则每次射击的命中率等于（）。

    • A、0.1
    • B、0.2
    • C、0.3
    • D、0.4

    正确答案:D

  • 第8题：

    两射手独立地向同一目标各射击一次，假设两射手的命中率分别为0.9和0.8，则目标被击中的概率为（）


    正确答案:0.98

  • 第9题：

    对同一目标进行三次独立地射击，第一、二、三次射击的命中率分别为0.4，0.5，0.7，则在三次射击中恰有一次击中目标的概率为（）。


    正确答案:0.36

  • 第10题：

    单选题
    某人独立地射击10次，每次射击命中目标的概率为0.8，随机变量X表示10次射击中命中目标的次数，则E（X2）等于（）．
    A

    64

    B

    65.6

    C

    66.6

    D

    80


    正确答案： C
    解析： 把每次射击看成是做一次伯努利试验，"成功"表示"命中目标"，"失败"表示"没有命中目标"，出现成功的概率p=0.8．于是，X服从参数n=10，p=0.8的二项分布．已知二项分布的数学期望与方差分别是 E(X)=np=10×0.8=8， D(X)=np(1-p)=10×0.8×0.2=1.6. 于是，由方差的计算公式推得 E(X2)=D(X)+［E(X)］2=1.6+82=65.6.故选(B). 本题借助于常用分布的数字特征来求E(X2)是比较方便的，因为常用分布的数学期望与方差可以作为已知值使用．如果用随机变量函数的数学期望的定义

  • 第11题：

    单选题
    甲、乙两人独立的对同一目标各射击一次，其命中率分别为0.6和0.5，现已知目标被命中，则它是甲射中的概率等于（）。
    A

    3/4

    B

    3/5

    C

    1/2

    D

    3/7

    E

    3/8


    正确答案： B
    解析： 暂无解析

  • 第12题：

    问答题
    22.甲、乙两人独立地各向同一目标射击一次，其命中率分别为0.6和O.7，求目标被命中的概率．若已知目标被命中，求它是甲射中的概率．

    正确答案：
    解析：

  • 第13题：

    某人连续向一目标独立射击(每次命中率都是3/4)，一旦命中，则射击停止，设X 为射击的次数，那么射击3次停止射击的概率是：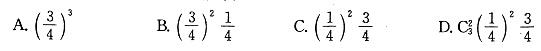


    答案：C
    解析：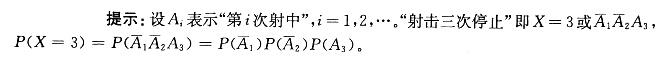

  • 第14题：

    甲、乙两人独立地向同一目标射击，甲、乙两人击中目标的概率分别为0．8，
    0．5，两人各射击1次，求至少有1人击中目标的概率．


    答案：
    解析：

  • 第15题：

    某人向同一目标独立重复射击，每次射击命中目标的概率为P(0
    A.3p(1－p)2
    B.6p(1－P)2
    C.3p2(1－P)2
    D.6p2(1－p)2

    答案：C
    解析：
    分析事件第4次射击恰好第2次击中目标可知，它表示前3次射击中有1次击中，同时，第四次命中。前3次射击中命中的次数服从二项分布，恰有l次击中的概率为C31p(1-p)3－1＝ 3p(1-p)2。所以整个事件的概率为3p(1-p)2×p＝3p2(1-p)2故选C。

  • 第16题：

    甲、乙两人独立的对同一目标各射击一次，其命中率分别为0.6和0.5，现已知目标被命中，则它是甲射中的概率等于（）。

    • A、3/4
    • B、3/5
    • C、1/2
    • D、3/7
    • E、3/8

    正确答案:A

  • 第17题：

    甲、乙两人独立地对同一目标射击一次，其命中率分别为0.6和0.5.现已知目标被命中，则它是甲射中的概率是（）


    正确答案:6/11

  • 第18题：

    在三次独立重复射击中，若至少有一次击中目标的概率为37/64，则每次射击击中目标的概率为（）。


    正确答案:1/4

  • 第19题：

    某人向同一目标独立重复射击，每次射击命中目标的概率为p（0＜p＜1），则此人第4次射击恰好第2次命中目标的概率为（）。

    • A、3p（1-p）2
    • B、6p（1-p）2
    • C、3p2（1-p）2
    • D、6p2（1-p）2

    正确答案:C

  • 第20题：

    一射手对同一目标独立地进行4次射击，假设每次射击命中率相同，若至少命中1次的概率为80/81，则该射手的命中率p=（）。


    正确答案:2/3

  • 第21题：

    单选题
    某人向同一目标独立重复射击，每次命中目标的概率为p（0＜p＜1），则此人第4次射击恰好第2次命中目标的概率为（　　）。
    A

    3p（1－p）2

    B

    6p（1－p）2

    C

    3p2（1－p）2

    D

    6p2（1－p）2


    正确答案： C
    解析：
    前3次射击中有1次命中目标的概率为C31p（1－p）2＝3p（1－p）2，由乘法公式得第4次射击恰好为第2次命中目标的概率为p·3p（1－p）2＝3p2（1－p）2。

  • 第22题：

    单选题
    甲乙两人独立地向同一目标各射击一次，命中率分别为0.8和0.6，现已知目标被击中，则它是甲射中的概率为：（）
    A

    0.26

    B

    0.87

    C

    0.52

    D

    0.75


    正确答案： B
    解析： 暂无解析

  • 第23题：

    填空题
    设X表示10次独立重复射击命中目标的次数，每次命中目标的概率为0.4，则E（X2）＝____。

    正确答案： 18.4
    解析：
    由题意可知，X～B（10，0.4），则
    E（X2）＝D（X）＋[E（X）]2＝10×0.4（1－0.4）＋（10×0.4）2＝18.4

相关内容