一个N点序列的N点DFT为该序列的DTFT在区间[0,π]上的等间隔采样。
题目
一个N点序列的N点DFT为该序列的DTFT在区间[0,π]上的等间隔采样。
相似考题
更多“一个N点序列的N点DFT为该序列的DTFT在区间[0,π]上的等间隔采样。”相关问题
-
第1题:
● 对于长度为m(m>1)的指定序列,通过初始为空的一个栈、一个队列后,错误的叙述是 (61) 。
(61)
A. 若入栈和入队的序列相同,则出栈序列和出队序列可能相同
B. 若入栈和入队的序列相同,则出栈序列和出队序列可以互为逆序
C. 入队序列与出队序列关系为1:1,而入栈序列与出栈序列关系是1:n(n≥1)
D. 入栈序列与出栈序列关系为1:1,而入队序列与出队序列关系是1:n(n≥1)
正确答案:D
试题(61)分析
本题考查数据结构基础知识。
队列的元素按特点是先进先出。对于队列,元素的进入次序和出队的次序相同,如,入队的序列为a、b、c,则出队的序列也为a、b、c。对于栈则不同,栈的运算特点是后进先出。若入栈序列为a、b、c,则出栈序列可能为a、b、c,a、c、b,b、a、c,b、c、a或者c、b、a,而c、a、b则不行,因此,入栈序列与出栈序列关系为1:1,而入队序列与出队序列关系为1:n(n1)。
参考答案
(61)D
-
第2题:
插入排序算法的主要思想是:每次从未排序序列中取出一个数据,插入已排序序列中的正确位置。Insert类的成员函数sort()实现了插入排序算法,请填空。
class Insert{
public:
Insert(int*b0,int n0):b(b0),n(n0){};//参数b0是某数组首地址,n是数组元素个数
void sort()
{//此函数假设已排序序列初始化状态只包含b[0],未排序序列初始为b[1]…b[n-1]
for(int i=1;i<n;++i)
{
int t=b[i];
int j;
for(______;j>0;--j)
{
if(t>=b[j-1])
break;
b[j]=b[j-1];
b[j]=t;
}
}
}
};
正确答案:j=i
j=i 解析:在函数sort()中,外层for循环中依次将数组b中的值赋值给变量t,然后在内层循环中依次与已经排序的数组元素进行比较,并在符合条件的位置插入该元素。“int t=b[i];”语句可知数组中有i个元素已经排序。因此,根据内层循环中的j>0;--j语句,知道内层循环是将当前的第i个元素与j个元素进行比较,前面已知数组中有i个元素已经排序,根据题干中的要求“插入已排序序列中”,即j=i。 -
第3题:
有限长序列的N点DFT相当于该序列的z变换在单位圆上的N点等间隔取样。()此题为判断题(对,错)。
参考答案:正确
-
第4题:
插入排序算法的主要思想是:每次从未排序序列中取出一个数据,插入到己排序序列中的正确位置。InsertSort类的成员函数sort()实现了插入排序算法。请将画线处缺失的部分补充完整。
class InsertSort{
public:
InsertSort(int* a0,int n0):a(a0),n(n0){}//参数a0是某数组首地址,n是数组元素个数
void sort()
{//此函数假设已排序序列初始化状态只包含a[0],未排序序列初始为a[1]…a[n-1]
for(int i=1;i<n;++i){
int t=a[i];
int j;
for(【 】;j>0;--j){
if(t>=a[j-1])break;
a[j]=a[j-1];}
a[j]==t;}}
protected:
int*a,n;//指针a用于存放数组首地址,n用于存放数组元素个数
};
正确答案:j=i
j=i 解析:本题考查的是插入排序算法。在sort()函数中是一个两重循环,外循环从1循环递增到n-1,即遍历未排序序列a[1]…a[n-1],取未排序序列中的第1个元素a[i] (i初值等于1)与已排序序列中的最后一个元素a[i-1]开始从后往前进行比较。内循环从后往前遍历已排序序列,使循环变量j的初值为i,则a[j-1]是已排序序列的最后一个元素。所以应该填j=i -
第5题:
一个栈的输入序列为123…n,若输出序列的第一个元素是n,输出第i(1≤i≤n)个元素是______。
A.不确定
B.n-i+l
C.i
D.n-i
正确答案:B
解析:栈的特点是先进后出,若输入序列为123…n,输出的第一个元素是n,则表明,所有元素都已入栈,则出栈顺序为:第1个元素为n,第2个元素为n-1,第3个元素为n-2,…,第i个元素是n-i+1。 -
第6题:
一个栈的输入序列为123…n,若输出的序列的第一个元素是n,输出的第i(1<=i<=n)个元素是【】
A.不确定
B.n-i+l
C.i
D.n-i
正确答案:B
[解析]因为输出序列的第一个元素是n,说明 n个元素全部进栈后才开始出栈,则输出第1个是n,第2个是n-1,第3个是n-2,……,第i 个是n-(i-1),即n-i+1. -
第7题:
若一个栈初始为空,其输入序列是1,2,3,…,n-1,n,其输出序列的第一个元素是k(1≤k≤n/2),则输出序列的最后一个元素是 ( ) 。A.1
B.n
C.n-1
D.不确定的答案:D解析:因为题目中没指出出栈的顺序,因此输出的最后一个元素是不确定的。 -
第8题:
设输入序列是1、2、3、……、n,经过栈的作用后输出序列的第一个元素是n,则输出序列中第i个输出元素是()A.n-1-i
B.n-i
C.n+1-i
D.不能确定答案:C解析:经过栈后的输出序列中第一个元素为n,代表从1至n是一次性全部人栈的,所以出栈序列刚好是入栈序列的倒序。 -
第9题:
设输入序列是1、2、3、……、n,经过栈的作用后输出序列的第一个元素是n,则输出序列中第i个输出元素是()。
- A、n-i
- B、n-1-i
- C、n+1-i
- D、不能确定
正确答案:C -
第10题:
DFT可以看成是时域N点映射到频域()点的一种映射关系。
正确答案:N -
第11题:
单选题某二叉树为单枝树(即非叶子节点只有一个孩子节点)且具有n个节点(n>1)则该二叉树()。A共有n层,每层有一个节点
B共有log2n层,相邻两层的节点数正好相差一倍
C先序遍历序列与中序遍历序列相同
D后序遍历序列与中序遍历序列相同
正确答案: D解析: 题考查数据结构中二叉树的基本概念和运算。 若二叉树为单枝树,那么n个节点就分布在n层上。遍历序列则与遍历方法和二叉树的形态有关。例如,对于三个节点的单枝二叉树(A、B、C的层次依次增高),其形态可为: [*] 考查它们的先序、中序和后序遍历序列,先序遍历序列都为A、B、C,而中序和后序遍历序列则有所不同。 -
第12题:
判断题若一个栈的输入序列为123…n,其输出序列的第一个元素为n,则其输出序列的每个元素ai一定满足ai=n-i+1。(i=1,2..…n)。A对
B错
正确答案: 对解析: -
第13题:
( 14 ) 插入排序算法的主要思想是 : 每次从未排序序列中取出一个数据 , 插入到已排序序列中的正确位置 。
InsertSort 类的成员函数 sort() 实现了插入排序算法。请将画线处缺失的部分补充完整。
class InsertSort{
public:
InsertSort(int* a0, int n0) :a(a0), n(n0) {} // 参数 a0 是某数组首地址, n 是数组元素个数
void sort( )
{// 此函数假设已排序序列初始化状态只包含 a[0] ,未排序序列初始为 a[1]...a[n-1]
for (int i=1; i
int t=a[i];
int j;
for ( 【 14 】 ; j>0; --j){
if (t>=a[j-1]) break;
a[j]=a[j-1];}
a[j]=t;}}
protected:
int *a, n; // 指针 a 用于存放数组首地址, n 用于存放数组元素个数
};
正确答案:
-
第14题:
● 某二叉树为单枝树(即非叶子结点只有一个孩子结点)且具有n个结点(n>1),则该二叉树 (40) 。
(40)
A. 共有n层,每层有一个结点
B. 共有log2n层,相邻两层的结点数正好相差一倍
C. 先序遍历序列与中序遍历序列相同
D. 后序遍历序列与中序遍历序列相同
正确答案:A
-
第15题:
下面算法是实现对n个整数的序列进行选择排序,其中序列的“长度”n为问题的规模。该算法的时间复杂度为(11)。 void select_sort(int a[],int n){ //将a中整数序列重新排列成从小到大有序的整数序列 for(i=0;i<n-1;++i){ j=i; for(k=i+1;k<n;++k)if(a[k]<a[j])j=k; if(j!=i){w=a[j];a[j];a[i];a[i]=w} )//select_sort
A.O(n2)
B.O(n3)
C.O(n4)
D.O(n)
正确答案:A
解析:算法中的控制结构是两重循环,所以基本操作是在内层循环中的“比较”,它的重复执行次数是:对时间复杂度而言,只需要取最高项,并忽略常数系数。 -
第16题:
如果一棵二叉树结点的前序序列是M、N、P、Q,后序序列是Q、P、N、M,则该二叉树结点的对称序序列( )。A.必为M、Q、P、NB.必为M、N、Q、PC.必为Q、N、P、MD.不能确定
正确答案:D
由前序序列可知,M为根节点。但是其他的结点的位置不好确定,因为在已知序列结果中,由于结点数少,左右结点的次序都可以构成已知结果,但对于对称序列来说,结果就不一样了。 -
第17题:
对于一个相始为空的栈,其入栈序列为 1、2、3、…、n (n>3) ,若出栈序列的第一个元素是 1,则出栈序列的第n 个元素( )。
A.可能是 2 ~ n中的任何一个B.一定是 2C.一定是 n-1D.一定是 n
正确答案:A
-
第18题:
若一个栈的输入序列是1,2,3,…,n,输出序列的第一个元素是n,则第i个输出元素是( )。A.不确定
B.n-i
C.n-i-l
D.n-i+l答案:D解析:此时,输出序列一定是输入序列的逆序,故第i个输出元素为n-i+l。 -
第19题:
求解两个长度为n的序列X和Y的一个最长公共子序列(如序列ABCBDAB和BDCABA的一个最长公共子序列为BCBA)可以采用多种计算方法。如可以采用蛮力法,对X的每一个子序列,判断其是否也是Y的子序列,最后求出最长的即可,该方法的时间复杂度为( )。经分析发现该问题具有最优子结构,可以定义序列长度分别为i和j的两个序列X和Y的最长公共子序列的长度为c[i,j],如下式所示。
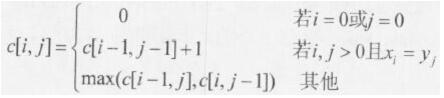
采用自底向上的方法实现该算法,则时间复杂度为(请作答此空)A.O(n^2)
B.O(n^21gn)
C.O(n^3)
D.O(n2^n)答案:A解析:蛮力法,对X的每一个子序列,判断是否也是Y的子序列,其中,长度为n的序列X共有2^n个子序列,判断其是否是Y的子序列时间是n,因此是n*2^n;采用动态规划法自底向上实现时,根据递归公式,实际是关于i和j的两重循环,因此时间复杂度是n^2. -
第20题:
若一个栈初始为空,其输入序列是1,2,3,…,n-1,n,其输出序列的第一个元素为k(1≤k≤「n/2」),则输出序列的最后一个元素是()。
- A、值为n的元素
- B、值为1的元素
- C、值为n-k的元素
- D、不确定的
正确答案:D -
第21题:
已知一个栈的输入序列为1,2,3,...,n,则其输出序列的第2个元素为n的输出序列的种数是()。
正确答案:n—1 -
第22题:
如果α的支撑集D是Zv的加法群的(4n-1,2n,n)差集,那么序列α就是Z2上周期为v的一个拟完美序列。
正确答案:错误 -
第23题:
填空题已知一个栈的输入序列为1,2,3,...,n,则其输出序列的第2个元素为n的输出序列的种数是()。正确答案: n—1解析: 暂无解析 -
第24题:
单选题设f(x)在x=0处满足f′(0)=f″(0)=…=f(n)(0),f(n+1)(0)>0,则( )。A当n为偶数时,x=0是f(x)的极大值点
B当n为偶数时,x=0是f(x)的极小值点
C当n为奇数时,x=0是f(x)的极大值点
D当n为奇数时,x=0是f(x)的极小值点
正确答案: C解析:
此题可用举例法判断。当n=1时(即n为奇数),f′(0)=0,f″(0)>0。由f″(0)>0知f′(x)在x=0处单调增加。又f′(0)=0,x<0时f′(x)<0;x>0时f′(x)>0。因此f(x)在x=0点处取得极小值。
当n=2时(即n为偶数),f′(0)=f″(0)=0,f‴(0)>0。由f‴(0)>0知,f″(x)在x=0处单调增加。因f″(0)=0,故f′(x)在x=0附近先减小后增加。f′(0)=0,故f(x)在x=0点处单调。因此x=0既不是f(x)的极大值也不是它的极小值。综上所述D项正确。
