itgle.com

2、目前讨论了六种类型的函数极限，不是每一类都具有局部有界性

题目

2、目前讨论了六种类型的函数极限，不是每一类都具有局部有界性

相似考题

1.设f(x)=sinx＋cos2x,则f(x)在(－∞,＋∞)为()A、奇函数B、偶函数C、单调函数D、有界函数

2.Excel提供了( )类函数，每一类有若干个不同的函数。A．7B．9C．11D．13

3.服从正态分布的随机误差都具有对称性、单峰性、抵偿性和有界性。()此题为判断题(对，错)。

4.下列关于Excel的函数说法正确的是( )。A．函数的形式是([参数1]，[参数2]，……)B．Excel提供了13类函数，每一类有若干个不同的函数C．函数中至少具备一个参数D．AVERAGE是求平均数函数

更多“2、目前讨论了六种类型的函数极限，不是每一类都具有局部有界性”相关问题

  • 第1题：


    A、有界函数
    B、无界函数
    C、单调函数
    D、周期函数

    答案：A
    解析：
    函数的有界性；

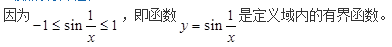
  • 第2题：


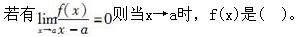    A.有极限的函数
    B.有界函数
    C.无穷小量
    D.比(x-a)高阶的无穷小

    答案：D
    解析：

  • 第3题：

    若有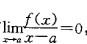则当x→a 时，f(x)是：
    A.有极限的函数 B.有界函数
    C.无穷小量 D.比(x-a)高阶的无穷小


    答案：D
    解析：
    提示:由极限运算法则，答案A、B、C均不成立，利用两个无穷小比较知识，当x→a时，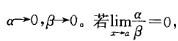
    称在x→a时，a是β的高阶无穷小，所以答案D成立。f(x)是比(x-a)高阶的无穷小。

  • 第4题：

    下列叙述正确的是()。

    A.有界函数的商必有界
    B.分段函数一定不是初等 函数
    C.无界函数必为无穷大
    D.有界函数与无穷大之和必为无穷大

    答案：D
    解析：

  • 第5题：

    讨论法教学有六种基本类型，其中（）是一种对某一主题具有丰富知识或代表性见解的若干名人员在讨论会协调者的主持之下发表意见，进行讨论的方法。

    • A、定型化讨论法；
    • B、自由讨论法；
    • C、集团讨论法；
    • D、专题讨论会法。

    正确答案:D

  • 第6题：

    以下叙述不对的是：我们讨论的重积分（）。

    • A、是一种和式的极限
    • B、是个连续函数
    • C、被积区域有限且被积函数有界
    • D、被积函数只要分段连续

    正确答案:B

  • 第7题：

    二元函数的极限与累次极限之间的关系是（）。

    • A、二元函数的极限存在则两累次极限都存在
    • B、累次极限就是二元函数的极限
    • C、两累次极限都存在则二元函数的极限存在
    • D、二元函数的极限和两累次极限都存在时，可用累次极限求二元函数极限

    正确答案:D

  • 第8题：

    函数的参数个数和类型都相同，只是返回值不同，这不是重载函数。


    正确答案:正确

  • 第9题：

    单选题
    以下叙述不对的是：我们讨论的重积分（）。
    A

    是一种和式的极限

    B

    是个连续函数

    C

    被积区域有限且被积函数有界

    D

    被积函数只要分段连续


    正确答案： D
    解析： 暂无解析

  • 第10题：

    单选题
    二元函数的极限与累次极限之间的关系是（）。
    A

    二元函数的极限存在则两累次极限都存在

    B

    累次极限就是二元函数的极限

    C

    两累次极限都存在则二元函数的极限存在

    D

    二元函数的极限和两累次极限都存在时，可用累次极限求二元函数极限


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    单调有界函数若有间断点，则其类型为（　　）.
    A

    必为第一类间断点

    B

    必为第二类间断点

    C

    第一类或第二类间断点

    D

    以上都不会


    正确答案： B
    解析：
    因函数单调有界，则它在间断点处的左、右极限必存在，故只可能是第一类间断点.

  • 第12题：

    单选题
    以下叙述正确的是：我们讨论的重积分（）。
    A

    被积区域可以无限

    B

    被积函数可以无界

    C

    被积函数必须连续

    D

    在有限的被积区域上被积函数有界


    正确答案： C
    解析： 暂无解析

  • 第13题：


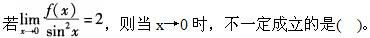    A.f(x)是有极限的函数
    B.f(x)是有界函数
    C.f(x)是无穷小量
    D.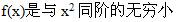

    答案：B
    解析：

  • 第14题：

    若有则当x→0时，f(x)是：
    (A）有极限的函数
    (B）有界函数
    (C）无穷小量
    （D）比（x-a）高阶的无穷小


    答案：D
    解析：
    ①若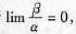就称β是比α高阶的无穷小，记作β=σ（α），并称α是比β低阶的无穷小
    ②若就称β是与α高阶的无穷小
    ③就称β是与α等价的无穷小，记作α~β，关于等价无穷小，有以下性质：
    且存在，则

    当x→0 时,有以下常用的等价无穷小：

  • 第15题：

    讨论函数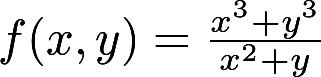 在点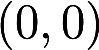 的重极限与累次极限。


    答案：
    解析：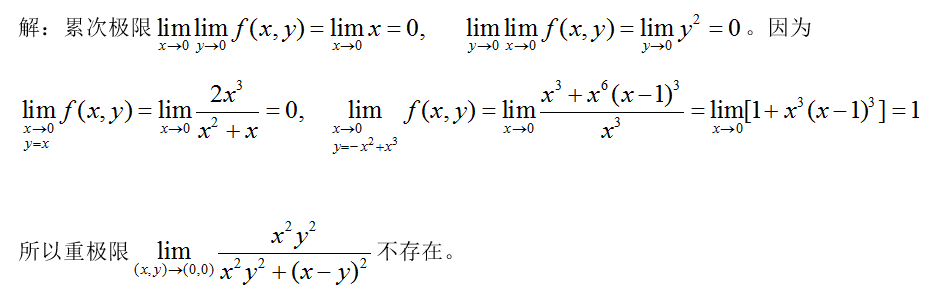

  • 第16题：

    设其中g(x)是有界函数，则f(x)在x=0点( )。

    A、极限不存在
    B、极限存在但不连续
    C、连续、但不可导
    D、可导

    答案：D
    解析：

  • 第17题：

    以下叙述正确的是：我们讨论的重积分（）。

    • A、被积区域可以无限
    • B、被积函数可以无界
    • C、被积函数必须连续
    • D、在有限的被积区域上被积函数有界

    正确答案:D

  • 第18题：

    若x点是函数的可去间断点，则在x点处函数（）。

    • A、左右极限都存在但不相等
    • B、左极限不存在
    • C、左右极限都存在且相等
    • D、右极限不存在

    正确答案:C

  • 第19题：

    函数在一点处的左右极限都存在，则函数在这一点的极限存在。


    正确答案:错误

  • 第20题：

    函数y=lg（x-1）在（1，2）上是有界函数。


    正确答案:错误

  • 第21题：

    单选题
    若x点是函数的可去间断点，则在x点处函数（）。
    A

    左右极限都存在但不相等

    B

    左极限不存在

    C

    左右极限都存在且相等

    D

    右极限不存在


    正确答案： A
    解析： 暂无解析

  • 第22题：

    单选题
    函数f（x）＝xsinx（　　）。
    A

    当x→∞时为无穷大量

    B

    在（－∞，＋∞）内有界

    C

    在（－∞，＋∞）内无界

    D

    当x→∞时有有限极限


    正确答案： D
    解析：
    （1）x＝（2kπ＋π/2）（k＝±1，±2，…）时，|k|无限增大时，|f（x）|＝|2kπ＋π/2|≥2π|k|－π/2大于任意给定的正数M，故f（x）＝xsinx在（－∞，＋∞）内无界。
    （2）当x＝2kπ时，f（x）＝0。
    综上所述，选C。

  • 第23题：

    单选题
    如果函数f（x）在点x0的某个邻域内恒有|f（x）|≤M（M是正数），则函数f（x）在该邻域内（　　）。
    A

    极限存在

    B

    连续

    C

    有界

    D

    不能确定


    正确答案： C
    解析：
    由函数有界的定义可知：设函数f（x）的定义域为D，数集X∈D。如果存在数K1使得f（x）≤K1对任意x∈X都成立则称函数f（x）在X上有上界。故选C项。

  • 第24题：

    判断题
    函数y=lg（x-1）在（1，2）上是有界函数。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

相关内容