itgle.com

一位篮球运动员投篮两次，两投全中的概率为0．375、；两投一中的概率为0．5，则他两投全不中的概率为 （ ）A.0．6875B.0．625C.0．5D.0．125

题目

一位篮球运动员投篮两次，两投全中的概率为0．375、；两投一中的概率为0．5，则他两投全不中的概率为 （ ）

A.0．6875

B.0．625

C.0．5

D.0．125

相似考题

1.同时抛掷3枚均匀的硬币，则恰好有两枚正面朝上的概率为（ ）A．0.125 B．0.25C．0.375 D．0.50

2.甲、乙两人独立的进行两次射击,每次射击甲命中概率为0.2,乙命中概率为0.5,X与Y分别表示甲、乙命中的次数,求X与Y的联合分布列。

3.已知某运动员每次投篮命中的概率低于40%。现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计算器算出0到9之间取整数值的随机数，指定1，2，3，4表示命中，5，6，，7，8，9，0表示不命中；再以每三个随机数为一组，代表三次投篮的结果。经随机模拟产生了20组随机数：907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989据此估计，该运动员三次投篮恰有两次命中的概率为A．0.35 B 0.25 C 0.20 D 0.15

4.一个骰子连续投2次，点数和为4的概率为_________。

更多“一位篮球运动员投篮两次，两投全中的概率为0．375、；两投一中的概率为0．5，则他两投全不中的概率为 （ ）A.0．6875B.0．625C.0．5D.0．125”相关问题

  • 第1题：

    市场上两只股票甲、乙。某天，股票甲上涨的概率为70%，股票乙上涨的概率为30%，两只股票同时上涨的概率为25%，则这一天两只股票至少有一只上涨的概率为( )。

    A．0.7

    B．0.3

    C．0.75

    D．1


    正确答案：D

  • 第2题：

    同时抛掷3枚均匀的硬币，则恰好有两枚正面向上的概率为

    A、0.5

    B、0.25

    C、0.125

    D、0.375


    正确答案:D

  • 第3题：

    某两地的通行必须经过两座桥,第一座桥需要维修的概率为0.05,第二座桥需要维修的概率为0.02,则这两地正常通行的概率为________。

    A．0.07

    B．0.01

    C．0.931

    D．0.069


    正确答案：C

  • 第4题：

    设试验成功的概率为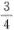,失败的概率为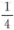,独立重复试验直到成功两次为止,求试验次数的数学期望.


    答案：
    解析：
    【解】设试验的次数为X，则X的分布律为

  • 第5题：

    某承包人面临A、B两项工程投标,因受本单位资源条件限制,只能选择其中一项工程投标,或者两项工程均不投标。根据过去类似工程投标的经验数据,A工程投高标的中标概率为0.3,投低标的中标概率为0.6,编制投标文件的费用为3万元；B工程投高标的中标概率为0.4,投低标的中标概率为O。7,编制投标文件的费用为2万元。各方案承包的效果、概率及损益情况见表7-2。
    【问题】2、试运用决策树法进行投标决策。


    答案：
    解析：
    2、第一步：画出决策树,标明各方案的概率和损益值,见图7—5。第二步：计算图中各机会点的期望值（可将计算结果标在各机会点上方）。点⑦：150×0.3+100×0.5+50×0.2=105万元点②：105×0.3-3×O。7=29.4万元点⑧：110×0.2+60×0.7+0×O.1=64万元点③：64×0.6-3×0.4=37.2万元点⑨：110×0.4+70×0.5+30×0.1=82万元点④：82×0.4-2×O.6=31.6万元点⑩：470×0.2+30×O.5-10×0.3=26万元点⑤：26×0.7-2×0.3=27.6万元点⑥：O第三步：选择最优方案。因为点③的期望值最大,故投A工程低标为最优方案。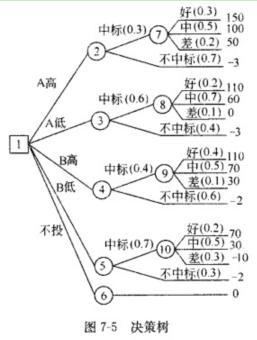

  • 第6题：

    投项目风险概率分析法中，应考虑的每种风险因素可能发生的概率总和必须（）


    正确答案:等于1

  • 第7题：

    假设随意地投掷一均匀骰子两次，则两次出现的点数之和为8的概率为（）

    • A、3/36
    • B、4/36
    • C、5/36
    • D、2/36

    正确答案:C

  • 第8题：

    甲投中篮球的概率0.5，乙投中的概率是0.6，各投两次，求甲乙投中次数相同的概率是（）。

    • A、0.63
    • B、0.37
    • C、0.36
    • D、0.64

    正确答案:B

  • 第9题：

    已知甲任意一次射击中靶的概率为0,5，甲连续射击3次，中靶两次的概率为（　）。


    正确答案:0.375

  • 第10题：

    填空题
    已知甲任意一次射击中靶的概率为0,5，甲连续射击3次，中靶两次的概率为（　）。

    正确答案： 0.375
    解析： 暂无解析

  • 第11题：

    单选题
    甲、乙两人下棋，甲胜的概率为40％，甲不输的概率为90％，则甲、乙两人下成和棋的概率为（　　）．
    A

    60％

    B

    30％

    C

    10％

    D

    50％


    正确答案： B
    解析：
    甲不输包括甲胜和甲与乙和棋两种情况，所以甲、乙两人下成和棋的概率为90％－40％＝50％．

  • 第12题：

    单选题
    某人投蓝，每次的命中率为0.7，现投5次，至少命中4次的概率（）
    A

    0.53

    B

    0.36

    C

    0.31

    D

    0.35


    正确答案： B
    解析： 暂无解析

  • 第13题：

    投两颗骰子，面朝上的点数之和为8的概率是（ ）。

    A． 1/6

    B． 5/36

    C． 1/9

    D． 1/13


    正确答案：B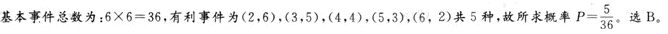

  • 第14题：

    投一枚硬币三次，问恰好有两次正面一次反面的概率是多少？（ ）

    A．4/5

    B．2/3

    C．3/8

    D．1/2


    正确答案：C
    一枚硬币投三次共有8种结果，用1表示为正面，0表示反面，则有(0，0，0)，(0，0，1)，(0，1，0)，(1，0，0)，(1，1，0)，(1，0，1)，(0，1，1)，(1，1，1)种结果，可以看到满足条件的结果有3种，概率是3/8。

  • 第15题：

    已知某篮球运动员每次投篮投中的概率为0．9．记X为他两次独立投篮投中的次数．
    ①求X的概率分布；
    ②求X的数学期望．


    答案：
    解析：
    ①设Ai=“第i次投篮投中”(i=1，2)，则两次独立投篮投中的次数X的可能取值为0，1，2．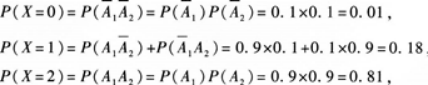

    从而X的概率分布为：

    ②E(X)=0×0．01+1×0．18+2x0．81=1．80．

  • 第16题：

    甲、乙两人轮流投篮。每人每次投一球。约定甲先投且先投中者获胜，一直到有人获胜或每人都已投球3次时投篮结束。设甲每次投篮投中的概率为1/3，乙每次投篮投中的概率为1/2，且各次投篮互不影响。则投篮结束时乙只投了两个球的概率为：

    A.1/27
    B.1/9
    C.4/27
    D.13/27

    答案：C
    解析：
    投篮结束时乙只投了两个球有两种情况：(1)乙在第二次投中；(2)甲在第三次投中。第

  • 第17题：

    某承包人面临A、B两项工程投标,因受本单位资源条件限制,只能选择其中一项工程投标,或者两项工程均不投标。根据过去类似工程投标的经验数据,A工程投高标的中标概率为0.3,投低标的中标概率为0.6,编制投标文件的费用为3万元；B工程投高标的中标概率为0.4,投低标的中标概率为O。7,编制投标文件的费用为2万元。各方案承包的效果、概率及损益情况见表7-2。
    【问题】1、简述决策树的概念。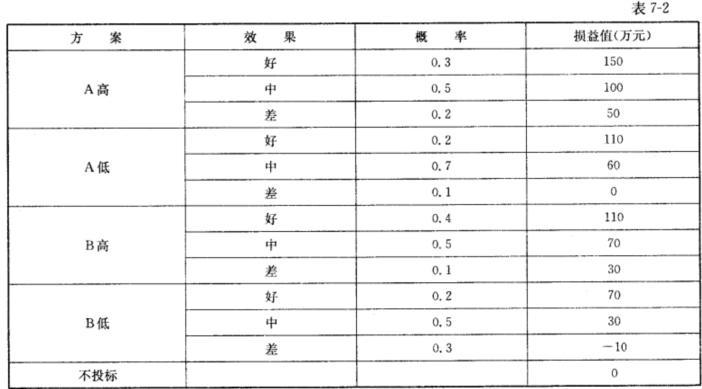


    答案：
    解析：
    1、决策树是以方框和圆圈为结点,并由直线连接而成的一种树枝形状的结构,其中：方框代表决策点,圆圈代表机会点：从决策点画出的每条直线代表一个方案,叫做方案枝,从机会点画出的每条直线代表一种自然状态,叫做概率枝。

  • 第18题：

    某人有一笔资金，他投入基金的概率为0.58，购买股票的概率为0.28，两项投资都做的概率为0.19，已知他已购买股票，再投入基金的概率为（）。


    正确答案:0.6786

  • 第19题：

    某人投蓝，每次的命中率为0.7，现投5次，至少命中4次的概率（）

    • A、0.53
    • B、0.36
    • C、0.31
    • D、0.35

    正确答案:A

  • 第20题：

    一对夫妇希望有两个或更多的小孩，预期他们将有两个男孩和一个女孩的概率为（）。

    • A、0.125
    • B、0.25
    • C、0.375
    • D、0.5

    正确答案:C

  • 第21题：

    已知甲任意一次射击中靶的概率为0.5，甲连续射击3次，中靶两次的概率为（）。

    • A、0.375
    • B、0.75
    • C、0.325
    • D、0.125

    正确答案:A

  • 第22题：

    填空题
    投项目风险概率分析法中，应考虑的每种风险因素可能发生的概率总和必须（）

    正确答案： 等于1
    解析： 暂无解析

  • 第23题：

    单选题
    已知甲任意一次射击中靶的概率为0.5，甲连续射击3次，中靶两次的概率为（）。
    A

    0.375

    B

    0.75

    C

    0.325

    D

    0.125


    正确答案： A
    解析： 暂无解析

相关内容