itgle.com

设函数f(x)=ax3＋bx2＋cx＋d，问常数a，b，c满足什么关系时，f(x)分别没 有极值、可能有一个极值、可能有两个极值?

题目

设函数f(x)=ax3＋bx2＋cx＋d，问常数a，b，c满足什么关系时，f(x)分别没 有极值、可能有一个极值、可能有两个极值?

相似考题

1.设f(x)=xe-x，求函数f(x)的极值（6分）

2.函数厂（x）具有连续的二阶导数，且f″（0）≠0，则x=0（ ）。A.不是函数f（x）的驻点 B.一定是函数f（x）的极值点 C.一定不是函数f（x）的极值点 D.是否为函数f（x）的极值点，还不能确定

3.下列命题中，正确的是( ).A.单调函数的导函数必定为单调函数 B.设f´(x)为单调函数，则f(x)也为单调函数 C.设f(x)在(a，b)内只有一个驻点xo，则此xo必为f(x)的极值点 D.设f(x)在(a，b)内可导且只有一个极值点xo，f´(xo)=0

4.设两函数f(x)及g(x)都在x=a处取得极大值，则函数F(x)=f(x)g(x)在x=a处( )。A.必取极大值 B.必取极小值 C.不可能取极值 D.是否取极值不能确定

更多“设函数f(x)=ax3＋bx2＋cx＋d,问常数a,b,c满足什么关系时,f(x)分别没 有极值、可能有一个极值、可能有 ”相关问题

  • 第1题：

    设函数f（x）在（a，b）内可微，且f′（x）≠0，则f（x）在（a，b）内（　　）。

    A、 必有极大值
    B、 必有极小值
    C、 必无极值
    D、 不能确定有还是没有极值

    答案：C
    解析：
    可导函数极值判断：若函数f（x）在（a，c）上的导数大于零，在（c，b）上的导数小于零，则f（x）在c点处取得极大值；若函数f（x）在（a，c）上的导数小于零，在（c，b）上的导数大于零，则f（x）在c点处取得极小值。即可导函数极值点处，f′（x）=0。函数f（x）在（a，b）内可微，则函数在（a，b）内可导且连续；又f′（x）≠0，则在（a，b）内必有f′（x）>0或f′（x）＜0，即函数f（x）在（a，b）内单调递增或单调递减，必无极值。

  • 第2题：

    设函数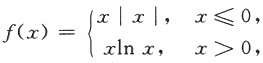则x=0是f(x)的

    A.A可导点，极值点B
    B.不可导点，极值点
    C.可导点，非极值点
    D.不可导点，非极值点

    答案：B
    解析：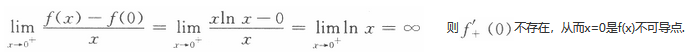

    又在x=0的左半邻域f(x)=x｜x｜<0=f(0)，
    　　在x=0的右半邻域f(x)=xln x<0=f(0)，
    　　则f(x)在x=0处取极大值，故应选(B).

  • 第3题：

    设f(x)处处连续，且在x=x1处有f'(x1)=0,在x=x2处不可导，那么（ ）。
    A.x=x1及x=x2都必不是f(x)的极值点
    B.只有x=x1是f(x)的极值点
    C.x=x1及x=x2都有可能是f(x)的极值点
    D.只有x=x2是f(x)的极值点


    答案：C
    解析：
    提示：驻点和导数不存在点都是极值可疑点。

  • 第4题：

    设函数f(x，y)=X2+Y2+xy+3，求f(x，y)的极值点与极值．


    答案：
    解析：

  • 第5题：

    函数厂（x）具有连续的二阶导数，且f″（0）≠0，则x=0（ ）。《》（ ）

    A.不是函数f（x）的驻点
    B.一定是函数f（x）的极值点
    C.一定不是函数f（x）的极值点
    D.是否为函数f（x）的极值点，还不能确定

    答案：D
    解析：
    由极值的必要条件可知，若f（x）在x=0处可导，且x=0是f（x）的极值点，则必有f′（0）=0。由题干无法确定f′（0）是否等于0，因此不能确定x=0是否为函数f（x）的极值点。

相关内容