itgle.com

在△ABC中，D、E分别是边AB、AC的中点，若BC＝5，则DE的长是（ ）。A．2.5B．5C．10D．15

题目

在△ABC中，D、E分别是边AB、AC的中点，若BC＝5，则DE的长是（ ）。

A．2.5

B．5

C．10

D．15

相似考题

1.△ABC中，AB=3，BC=4，则AC边的长满足（ ）。A．AC=5B．AC>1C．AC<7D．1<AC<7

2.改良Barthel指数评分中,若进餐情况为需要部分帮助才能完成,则该项得分为()A.0分B.5分C.10分D.15分E.20分

3.在 △ABC中，∠C=90°，AB=10。（1）∠A=30°，求BC，AC（精确到0.01）；（2）∠A=45°，求BC，AC（精确到0.01）。

4.改良Barthel指数评分中,若小便偶尔失禁,则该项得分为()A.0分B.5分C.10分D.15分E.20分

更多“在△ABC中,D、E分别是边AB、AC的中点,若BC=5,则DE的长是( )。 A.2.5 B.5 C.10 D.15 ”相关问题

  • 第1题：

    下列关于函数依赖的描述，错误的是（ ）。

    A.若A→B，B→C，则A→C B.若A→B，A→C，则A→BC C.若B→A，C→A，则BC→A D.若BC→A，则B→A，C→A


    正确答案：D

  • 第2题：

    锐角三角形ABC中，sinA=√5/5，D为BC边上的点，若△ABD 和△ACD的面积分别为2和4，过D作DE ⊥AB于E，DF⊥AC于F，


    答案：
    解析：

  • 第3题：

    如图所示，△ABC中DE∥BC，且BO和CO分别是∠ABC和∠ACB的角平分线。已知AB=25.4 cm，BC=24.5 cm，AC=20 cm。问△ADE的周长是多少？

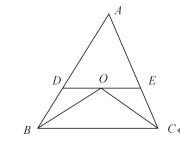
    A．45.4 cm B．45.1 cm C．44.8 cm D．44.5 cm


    答案：A
    解析：
    根据题意可知，DO=BD，OE=EC，则△ADE的周长=AB+AC=45.4 cm。

  • 第4题：

    在△ABC中，已知AB＝5，AC＝3，∠A＝120°，则BC长为



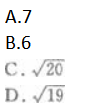    答案：A
    解析：

  • 第5题：

    在△ABC中，若AB=3，A=45°，C=30°，则BC=（　　）



    答案：C
    解析：

  • 第6题：

    在 ABC中，∠ABC=600，AB=4，BC=6，则AC=（）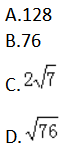


    答案：C
    解析：

  • 第7题：

    如，在直角三角形ABC中，AC=4，BC=3，DE//BC，已知梯形BCDE的面积为3，则DE长为（ ）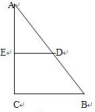



    答案：D
    解析：

  • 第8题：

    在△ABC中，∠C=90o，AC=8，BC=6，则△ABC的外接圆直径的长为__________ 。


    答案：
    解析：
    10

  • 第9题：

    如图，Rt△ABC中，AB=6，BC=4，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为__________。



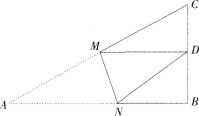    答案：
    解析：

  • 第10题：

    分别用分析法，综合法证明如下命题。
    命题：如图：三角形ABC的角B和角C的角平分线相交于点0，过点O作平行于底边BC的直线，交AB边于点D，交AC边于点E，则DE=BD+EC。



    答案：
    解析：
    证明：(1)分析法证明：要证DE=BD+EC．
    需证OD=BD，OE=CE，
    需证∠DBO=∠DOB,∠ECO=∠EOC，
    显然由已知OB为∠DBC的平分线，OC为∠ECB的平分线，且DE∥BC，所以∠DBO=∠DOB,∠ECO=∠EOC,所以命题成立。
    (2)综合法证明：
    ∵OB为∠DBC的平分线，OC为1ECB的平分线，且DE∥BC，
    ∴∠DBO=∠OBC=∠DOB,∠EC0=∠BC0=∠EOC,
    ∴BD=OD．EC=OE。
    又∵DE=OD+DE
    ∴DE=BD+EC。

  • 第11题：

    有一镗削工件，三孔ABC的坐标尺寸如图，为检验上的需要，计算三孔ABC的中心距尺寸，正确的是（）。

    • A、AB=26.93，BC=23.35，AC=27.2
    • B、AB=26.93，BC=20.23，AC=26.5
    • C、AB=25.03，BC=23.35，AC=27.2
    • D、AB=25.03，BC=20.23，AC=27.2

    正确答案:A

  • 第12题：

    单选题
    在△ABC中，AC＝5，中线AD＝7，则AB边的取值范围是（　　）。
    A

    1＜AB＜29

    B

    4＜AB＜24

    C

    5＜AB＜19

    D

    9＜AB＜19


    正确答案： D
    解析：
    延长AD到E，使DE＝AD，则ABEC为平行四边形，所以BE＝5，AE＝14，因此9＜AB＜19。

  • 第13题：

    设A、B、C为随机事件，则( )。

    A.P(A-B-C)=P(A)-P(AB)-P(AC)-P(BC)+P(ABC)
    B.P(A-B-C)=P(A)-P(AB)-P(AC)+P(ABC)
    C.P(A-B-C)=P(A)-P(AB)-P(BC)+P(ABC)
    D.P(A-B-C)=P(A)-P(AC)-P(BC)+P(ABC)

    答案：B
    解析：

  • 第14题：

    如图,D是△ABC内的一点，BD⊥CD，AD=6，BD=8，CD=6，E，F，G，H分别是AB，AC，CD， BD的中点．则四边形EFGH的周长是()。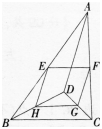

    A.12
    B.14
    C.15
    D.16

    答案：D
    解析：
    因为BD⊥CD，BD=8，CD=6，由勾股定理可知BC=10。由三角形中位线定理可知EH=FG=

  • 第15题：

    平行四边形ABCD如右图所示，E为AB上的一点，F、G分别是AC和DE、DB的交点。若AB=3AE，则四边形BEFG与ABCD的面积之比是：

    A.2︰7
    B.3︰13
    C.4︰19
    D.5︰24

    答案：D
    解析：
    第一步，本题考查几何问题，属于平面几何类，用赋值法解题。
    第二步，题干没给出具体数值，可以采用赋值法解题。赋值AB=3，平行四边形ABCD的高为4，则AE=1；由于△AEF相似于△CDF，则两个三角形的高之比为AE：DC=1︰3，可知△AEF的高为
    4*1/4=1。△ABG与△CDG全等，则△ABG的高为4÷2=2。
    第三步，四边形BEFG面积=△ABG面积-△AEF面积=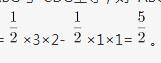

    四边形ABCD面积=3×4=12，两者之比为 ︰12=5︰24。
    因此，选择D选项。

  • 第16题：

    在△ABC中，AB=2，BC=3，B=60°，BD为AC边上的高．求AC，BD．


    答案：
    解析：

  • 第17题：

    在△ABC中，AB=2，BC=3，B=60°．求AC及△ABC的面积．


    答案：
    解析：
    解：由余弦定理得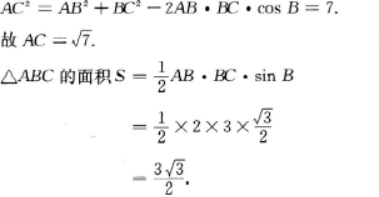

  • 第18题：

    在三角形ABC，AB=4，AC=6，BC=8，D为BC的中点，则AD=




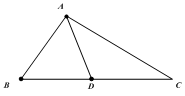
    答案：B
    解析：

  • 第19题：

    如右图所示，在△ABC：中，D为AC的中点，E在BC上，且 BE ： EC=1 ： 2，AE与BD交于F。则△BEF与四边形EFDC 的面积之比为（ ）。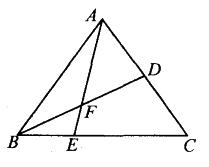

    A. 1 : 3 B. 1 ： 4
    C. 1 ： 5 D. 1 ： 6


    答案：C
    解析：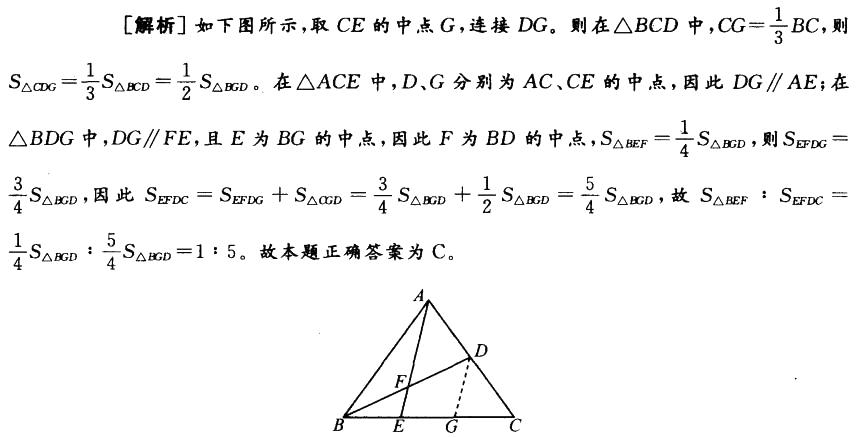

  • 第20题：

    如图1，在△ABC中，BC = 8 cm，AB的垂直平分线交AB于点Ｄ， 交边AC于点E，△BCE的周长等于18 cm，则AC的长等于（ ）

    A、6cm　
    B、8cm
    C、10cm　　
    D、12cm

    答案：C
    解析：

  • 第21题：

    如图在ΔABC中，DE∥BC，若AD：DB=1：3，DE=2，则BC等于( )。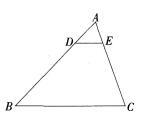

    A.8
    B.6
    C.4
    D.2

    答案：A
    解析：
    由于DE∥BC,所以DE：BC=AD：AB，又由AD:DB=1：3，所以AD：AB=1:4，由DE=2得BC=8。

  • 第22题：

    (10分)如图，几何体A1B1C1-ABC中，AB=AC，AB⊥AC，棱AA1，BB1，CC1都垂直于面ABC，BC=AA1=2BB1=2CC1=4，D为B1C1的中点，E为A1D的中点。
    求证：(1)AE⊥BC；(3分)
    (2)求异面直线AE与DC所成角的余弦值。(7分)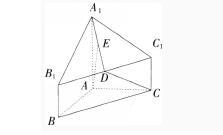


    答案：
    解析：

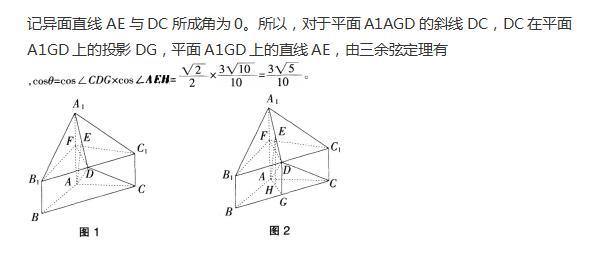
  • 第23题：

    在Z中若（a，c）=1，（b，c）=1，则可以得出哪两个数是素数？（）

    • A、（abc，a）=1
    • B、（ac，bc）=1
    • C、（abc，b）=1
    • D、（ab，c）=1

    正确答案:D

相关内容