举例说明不等式的基本性质与等式的基本性质的区别。
题目
举例说明不等式的基本性质与等式的基本性质的区别。
相似考题
更多“举例说明不等式的基本性质与等式的基本性质的区别。 ”相关问题
-
第1题:
“基本不等式”是高中数学教学中的重要内容,请完成下列任务:
(1)在“基本不等式”起始课的“教学重点”设计中,有两种方案:①强调基本不等式在求数值中的应用,将基本不等式的应用作为重点。②强调基本不等式的背景,过程与意义,将学生感受和体验“基本不等式”中“基本”的意义作为教学重点。你赞同哪种方案?简述理由。(2)给出的几何解释。
(3)为了让高中生充分认识“基本不等式”中“基本”的意义,作为教师应该对此有多个维度的理解,请至少从两个维度谈谈你对“基本”意义的认识。答案:解析:


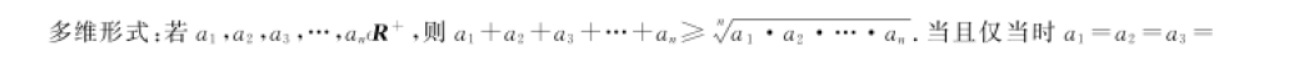
-
第2题:
【填空题】情绪的性质与事件的性质基本一致;情绪的()与事件的大小基本一致。
B -
第3题:
解不等式主要是依据不等式的性质进行恒等变形的。
B 因为2,3是方程 的两个根,所以 所以不等式 就是不等式 ,其解集为 . -
第4题:
19、线性规划模型可以有不等式约束条件,但不等式约束条件只能是小于等于的不等式。
错误 -
第5题:
2、在不等式的证明中,有一种方法是构造函数,通过对这个函数性质的研究,指向不等式的证明,这种方法本质上说就是一般化的方法。
分析法 试题分析:根据题意,由于该命题证明不等式 条件入手不能推出结论,则考虑从结论入手来逆推法来求解结论成立的充分条件即可,故该试题适合的最好方法是分析法,故答案为分析法。 点评:主要是考查了运用分析法来证明不等式的方法的运用,属于基础题。
