itgle.com

对分组数据计算加权算术平均数时，其平均数数值会受到()影响。A:极端值 B:组内极差 C:各组数值大小 D:组内标准差 E:各组频数多少

题目
对分组数据计算加权算术平均数时，其平均数数值会受到()影响。

A:极端值
B:组内极差
C:各组数值大小
D:组内标准差
E:各组频数多少
相似考题

1.下列关于算术平均数的说法中，正确的是（ ）。 A．算术平均数主要适用于数值型数据，但不适用于品质数据 B．算术平均数包括简单算术平均数和加权算术平均数等 C．算术平均数是按数据的大小顺序或出现频数的多少确定的集中趋势的代表值 D．算术平均数既适用于品质数据，也适用于数值数据 E．算术平均数是全部数据的算术平均

2.计算和应用平均数时，受数据中极端数值影响的平均数是（ ）。A．调和平均数B．几何平均数C．众数D．中位数E．算术平均数

3.由相对数或平均数计算平均数时，如果掌握的权数资料是相对数或平均数的分子项数值，则采用的计算方法应该是( )。A．简单算术平均数B．加权算术平均数C．加权调和平均数D．几何平均数

4.对于经分组整理的数据，其算术平均数会受到( )等因素的影响。A．各组数值的大小B．各组分布频数的多少C．组数D．数据个数E．极端值

更多“对分组数据计算加权算术平均数时，其平均数数值会受到()影响。”相关问题

  • 第1题：

    由于简单算术平均数和加权算术平均数在计算时,都是对全部数据进行计算,如果现象中存在着极端值时,平均数将受影响,出现偏高或偏低现象,影响对总体推断的准确性。所以,在调查资料数值分布比较均匀,数据波动幅度不大时,可以采用计算平均数的方式,来揭示现象的一般规律。如果不符合上述条件,一般可以采用计算中位数和众数的方法。()

    此题为判断题(对，错)。


    参考答案：正确

  • 第2题：

    根据未分组管理的原始数据计算的算术平均数是（ ）。

    A．加权算术平均数

    B．简单算术平均数

    C．几何平均数

    D．不变算术平均数


    正确答案：B

  • 第3题：

    计算和应用平均数时，不受数据中极端数值影响的平均数是( )。

    A．简单算术平均数

    B．几何平均数

    C．众数

    D．中位数

    E．加权算术平均数


    正确答案：CD

  • 第4题：

    根据分组整理的数据计算算术平均数的是()。

    A:加权算术平均数
    B:简单算术平均数
    C:几何平均数
    D:不变算术平均数

    答案：A
    解析：
    加权算术平均数主要用于处理经分组整理的数据，计算公式为：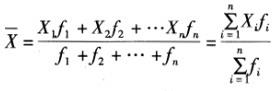

    式中，Xi表示各组的组中值；fi表示各组的频数。

  • 第5题：

    下列关于算术平均数的说法中，正确的有()。

    A:算术平均数主要适用于数值型数据，但不适用于品质数据
    B:算术平均数包括简单算术平均数和加权算术平均数等
    C:算术平均数是按数据的大小顺序或出现频数的多少确定的集中趋势的代表值
    D:算术平均数既适用于品质数据，也适用于数值型数据
    E:算术平均数是全部数据的算术平均

    答案：A,B,E
    解析：
    本题考查算术平均数的相关内容。算术平均数主要适用于数值型数据，但不适用于品质数据。位置平均数是指按数据的大小顺序或出现频数的多少确定的集中趋势的代表值。选项CD说法有误。

  • 第6题：

    对于经分组整理的数据，其算术平均数会受到()等因素的影响。

    A:各组数值的大小
    B:各组分布频数的多少
    C:组数
    D:数据个数
    E:极端值

    答案：A,B,E
    解析：
    本题考查算术平均数。算术平均数同时受到两个因素的影响：各组数值的大小和各组分布频数的多少；算数平均数也易受极端值的影响。所以选ABE。

  • 第7题：

    加权算术平均数适合于分组的统计资料，它受到变量和权数两个因素影响。权数对平均数起权衡轻重的作用，权数对平均数的影响取决于频率权数。（）


    答案：对
    解析：

  • 第8题：

    请分别写出简单算术平均数、加权算术平均数、加权调和平均数的计算公式并分别说明其应用条件。

    略

  • 第9题：

    计算加权算术平均数时，若对各组次数均扩大10倍，则算术平均数的数值（）

    • A、扩大10倍
    • B、缩小10倍
    • C、不变
    • D、说不定

    正确答案:C

  • 第10题：

    单选题
    在测度集中趋势时，不受数据中极端数值影响的是（　　）。
    A

    加权算术平均数

    B

    几何平均数

    C

    中位数

    D

    算术平均数


    正确答案： A
    解析：
    中位数是一个位置代表值，不受极端值的影响，抗干扰性强。

  • 第11题：

    单选题
    对于由观测变量的各个分组和各组变量总值顺序排列的分组分布表，计算算术平均数需采用的计算公式为（）
    A

    简单算术平均数

    B

    加权算术平均数

    C

    简单调和平均数

    D

    加权调和平均数


    正确答案： D
    解析： 暂无解析

  • 第12题：

    多选题
    计算和应用平均数时，受数据中极端数值影响的平均数是（）。
    A

    调和平均数

    B

    几何平均数

    C

    众数

    D

    中位数

    E

    算术平均数


    正确答案： D,C
    解析： 中位数是数据按照大小排列之后位于中间的那个数（如果样本量为奇数），或者中间两个数目的平均（如果样本量为偶数）；众数是数据中出现次数或出现频率最多的数值。中位数和众数是根据标志值在总体中所处的特殊位置来确定的平均数，也称作位置平均数，它们不受数据中极端数值的影响。

  • 第13题：

    对分组数据汁算加权算术平均数时，其平均数数值会受到（ ）等因素的影响。A．极端值B．组内极差C．各组数值大小D．组内标准差E．各组频数多少


    正确答案：ACE
    计算和运用算术平均数需注意：第一，算术平均数同时受到两个因素的影响，一个是各组数值的大小，另一个是各组分布频数的多少。第二，算术平均数易受极端值的影响。

  • 第14题：

    根据分组管理的数据计算算术平均数是（ ）。

    A．加权算术平均数

    B．简单算术平均数

    C．几何平均数

    D．不变算术平均数


    正确答案：A

  • 第15题：

    对分组数据计算加权算术平均数时，其平均数值会受到()等因素的影响。

    A:组内极差
    B:极端值
    C:组内标准差
    D:各组数值大小
    E:各组频数多少

    答案：B,D,E
    解析：
    本题考查算术平均数的相关知识。计算和运用算术平均数须注意：(1)算术平均数同时受到两个因素的影响：各组数值的大小；各组分布频数的多少。(2)算术平均数易受极端值的影响。

  • 第16题：

    以下有关平均数的说法，正确的有()。

    A:算术平均数是集中趋势最主要的测度值
    B:简单算术平均数主要用于处理未分组的原始数据
    C:加权算术平均数主要用于处理经分组整理的数据
    D:算术平均数易受极端值的影响
    E:各组数值的大小在加权算术平均数中起着权衡轻重的作用

    答案：A,B,C,D
    解析：
    选项E，算术平均数同时受到两个因素的影响，一个是各组数值的大小，另一个是各组分布频数的多少。频数在加权算术平均数中起着权衡轻重的作用。

  • 第17题：

    计算运用算术平均数时，其平均数数值会受到( )等因素的影响。

    A.极端值
    B.组内极差
    C.各组数值大小
    D.组内标准差
    E.各组频数多少

    答案：A,C,E
    解析：
    此题考察计算和运用算术平均数的三个影响因素。各组数值的大小、各组分布频数的多少、极端值的影响。

  • 第18题：

    在测度集中趋势时，不受数据中极端数值影响的是()。

    A:加权算术平均数
    B:几何平均数
    C:中位数
    D:算术平均数

    答案：C
    解析：
    中位数是一个位置代表值，不受极端值的影响，抗干扰性强。

  • 第19题：

    对分组数据计算加权算术平均数时，其平均数数值会受到（　　）等因素的影响。

    A.组内极差
    B.极端值
    C.组内标准差
    D.各组数值大小
    E.各组频数多少

    答案：B,D,E
    解析：
    计算和运用算术平均数须注意：①算触平均数同时受到两个因素的影响：各组数值的大小；各组分布频数的多少。②算术平均数易受极端值的影响。

  • 第20题：

    对于由观测变量的各个分组和各组变量总值顺序排列的分组分布表，计算算术平均数需采用的计算公式为（）

    • A、简单算术平均数
    • B、加权算术平均数
    • C、简单调和平均数
    • D、加权调和平均数

    正确答案:D

  • 第21题：

    计算和应用平均数时，受数据中极端数值影响的平均数是（）。

    • A、调和平均数
    • B、几何平均数
    • C、众数
    • D、中位数
    • E、算术平均数

    正确答案:A,B,E

  • 第22题：

    多选题
    对分组数据计算加权算术平均数时，其平均数值会受到（　）等因素的影响。
    A

    组内极差

    B

    极端值

    C

    组内标准差

    D

    各组数值大小

    E

    各组频数多少


    正确答案： D,C
    解析： [答案]：BDE
    [解析]：本题考查算术平均数的相关知识。计算和运用算术平均数须注意(1)算术平均数同时受到两个因素的影响：各组数值的大小;各组分布频数的多少。(2)算术平均数易受极端的影响。参见教材P192。

  • 第23题：

    多选题
    适用于数值型数据，且不受极端值影响的有（  ）。
    A

    众数

    B

    中位数

    C

    简单算术平均数

    D

    加权算术平均数

    E

    极差


    正确答案： A,B
    解析：

相关内容