itgle.com

已知一个等差数列的第五项等于10，前三项的和等于3，那么这个等差数列的公差为（ ）A.3 B.1 C.-1 D.-3

题目
已知一个等差数列的第五项等于10，前三项的和等于3，那么这个等差数列的公差为（ ）

A.3
B.1
C.-1
D.-3
相似考题

1.等差序列填充的步骤为()。A.先选定两个单元格的填充区域，然后输入等差数列的前两个值，再拖动区域的填充柄；B.先选定两个单元格的填充区域，然后输入等差数列的前两个值，再拖动区域的边框C.先选定等差数列的填充区域，然后输入等差数列的第一个值，再单击菜单栏中"视图一"填充"；D.先选定等差数列的填充区域，然后输入等差数列的第一个值，再单击菜单栏中"格式"--"填充"。

2.已知一个等差数列的首项为1，公差为3，那么该数列的前5项和为 （ ）A.35B.30C.20D.10

3.在等差数列{an}中，a5=6，前5项和等于20，则前10项的和等于 （ ）A.75B.65C.125D.60

4.已知等差数列{an}的首项与公差相等，{an）的前n项的和记作Sn，且S20=840．（I）求数列{an}的首项a1及通项公式；（Ⅱ）数列{an}的前多少项的和等于847.

更多“已知一个等差数列的第五项等于10，前三项的和等于3，那么这个等差数列的公差为（ ）”相关问题

  • 第1题：

    一个等差数列共有2n-1项，所有奇数项的和为36，所有偶数项的和为30，那么n的值为（ ）。 A．5 B．6 C．10 D．11


    正确答案：B
    所有奇数项的和减去所有偶数项的和得到36-30=6，即为中位数，则数列一共有(36+30)+6=11项，故n=(11+1)÷2=6，应选择B。

  • 第2题：

    已知公差为2的正整数等差数列为an，则该数列满足不等式7/16＜an/5＜398/9的所有项的和为（ ）

    A．12320

    B．12430

    C．12432

    D．12543


    正确答案：A
    13.【解析】公差为2的正整数数列为奇数列，满足条件的an最小为3，最大为221，故和为(3+221)×[(221-3)÷2+1]。故选A。

  • 第3题：

    已知等差数列{an}的公差是2，且a1+a2+a3+…+a100=100，那么a4+a8+a12+…+a100=


    答案：
    解析：
    ∵等差数列{an}的公差是2，且a1+a2+a3+…+a100=100=100a1+ 100×99/2 ×2， ∴a1 =-98，式子a4+a8+a12+…+a100 中共有25项，首项为a4，公差为4×2=8． ∴a4+a8+a12+…+a100 =25（a1 +6）+ (25×24)/2 ×(4×2)=25[（a1 +6）+12×8]=25×4=100， 故选100．

  • 第4题：

    设等差数列{an}的公差d不为0，a1=4d，若ak是a1与a2k的等比中项．则k等于( )。

    A.1
    B.3
    C.5
    D.7

    答案：B
    解析：
    等差数列{an}的通项公式an=4d+(n-1)d=(n+3)d，由ak2=a1a2k得(k+3)2d2=4d·(2k+3)d，整理得关于k的一元二次方程k2-2k-3=0，解之得k=3(负值舍去)。

  • 第5题：

    已知公差为2的正整数等差数列为an ，则该数列满足不等式7/16 ＜an/5 ＜398/9 的所有项的和为（ ）

    A. 12320
    B. 12430
    C. 12432
    D. 12543

    答案：A
    解析：
    公差为2的正整数数列为奇数列，满足条件的an 最小为3，最大为221，故和为(3+22)*[(221-3)/2+1]/2=12320 。故答案为A。

  • 第6题：

    已知等差数列前n项和
    (Ⅰ)求这个数列的逋项公式；
    (II)求数列第六项到第十项的和．


    答案：
    解析：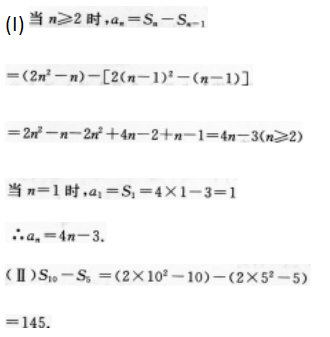

  • 第7题：

    已知三角形的三边边长组成公差为1的等差数列，且最大角是最小角的二倍，求三之长。


    答案：
    解析：
    三角形的三边边长分别为4，5，6

  • 第8题：

    已知某等差数列共有20项,其奇数项之和为30,偶数项之和为40,则其公差为（ ）.

    A.5
    B.4
    C.3
    D.2
    E.1

    答案：E
    解析：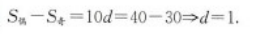

  • 第9题：

    案例：

    在等差数列的习题课教学中，教师布置了这样一个问题：等差数列前10项和为100，前100项和为10，求前110项的和。

    两位学生的解法如下：

    学生甲：设等差数列的首项为a1，公差为d，则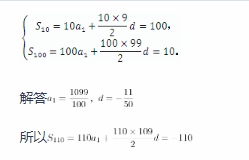

    学生乙：设等差数列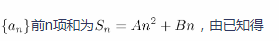


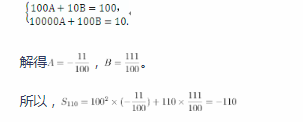
    针对上述解法，一些学生提出了自己的想法。

    （1）请分析学生甲和学生乙解法各自的特点，并解释学生乙设的理由。（12分）

    （2）请验证(*)中结论是否成立。


    答案：
    解析：
    本题主要从“等差数列”相关知识入手，考查等差数列的相关概念、等差数列的通项公式、求和公式等基层知识，教学工作的基本环节，常用的教学方法，以及课堂导入技巧等基本知识与技能。

  • 第10题：

    关于倒年系数法的理解与应用说法正确的有（）

    • A、折旧系数是等差数列，但折旧额不一定
    • B、按年序折旧系数与折旧额都是等差数列
    • C、折旧额是等差数列，但折旧系数不一定
    • D、折旧额总和等于原设备购入价减去残值

    正确答案:B

  • 第11题：

    有一等差数列，共8项。已知公差为2，第2项为4，求第三项的值。答案中含有的信息量是（）。

    • A、log1
    • B、log2
    • C、log8
    • D、log（1/8）

    正确答案:A

  • 第12题：

    单选题
    已知等差数列{an}满足a2＋a4＝4，a3＋a5＝10，则它的前10项的和S10＝（　　）。
    A

    138

    B

    135

    C

    95

    D

    23


    正确答案： D
    解析：
    由a2＋a4＝4，a3＋a5＝10得，a1＝4，d＝3，故S10＝10a1＋45d＝40＋135＝95。

  • 第13题：

    标准等差数列的计算公式为(row(a1)－1)*公差。()

    此题为判断题(对，错)。


    答案：正确

  • 第14题：

    设Sn为等差数列｛an｝的前n项和，若S3=3，S6=24，则a9= 。


    正确答案：
    15

  • 第15题：

    已知等差数列{an}中，a1=21，Sn是它的前n项之和，S7=S15。
    (1)求Sn；
    (2)这个数列的前多少项之和最大 求出最大值。


    答案：
    解析：
    (1)设等差数列的公差为d，由题意可得：



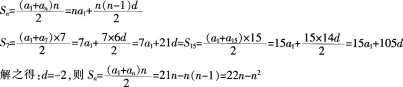
    (2)Sn=22n-n2=-(n-11)2+121，当n=11时，数列之和最大，最大值为121。

  • 第16题：

    一个等差数列有2n—1项，所有偶数项的和为40，所有奇数项的和为50，那么该数列共有( )项。

    A. 7
    B. 8
    C. 9
    D. 10

    答案：C
    解析：

  • 第17题：

    设直角三角形的三边为a、b、c，内切圆直径为2r，外接圆直径为2R，若a、b、c成等差数列，
    求证：
    (I)内切圆的半径等于公差；
    (Ⅱ)2r、a、b、2R也成等差数列．


    答案：
    解析：
    (I)由题意知，2R=c，∵a+b=r+r+χ+y，(如图a=χ+r，b=y+r)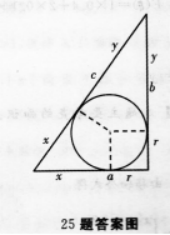
    又∵c=χ+y→2r=a+b-c.
    设公差为d，则三边为b-d，b，b+d，则有(b-d)2+b2=(b+d)2
    得6=4d，即三边a、b、c分别等于3d、4d、5d，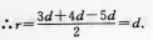

    (Ⅱ)由(I)可知2r、a、b、2R分别为2d、3d、4d、5d，∴其也为等差数列．

  • 第18题：

    等差数列{an)中，已知前15项之和S15＝90，则a1＋a15＝＝（　　）

    A.8
    B.10
    C.12
    D.14

    答案：C
    解析：

  • 第19题：

    已知{an}是等差数列,a1+a2=4,a7+a8=28,则该数列前10项和S10等于（ ）

    A.64
    B.100
    C.110
    D.130
    E.120

    答案：B
    解析：

  • 第20题：

    案例：

    在等差数列的习题课教学中，教师布置了这样一个问题：等差数列前10项和为100，前100项和为10，求前110项的和。

    两位学生的解法如下：

    学生甲：设等差数列的首项为a1，公差为d，则


    针对上述解法，一些学生提出了自己的想法。

    （1）请分析学生甲和学生乙解法各自的特点，并解释学生乙设的理由。（12分）

    （2）请验证(*)中结论是否成立。（8分）


    答案：
    解析：

  • 第21题：

    一个等差数列首项为32，该数列从第15项开始小于1，则此数列的公差d的取值范围是()．?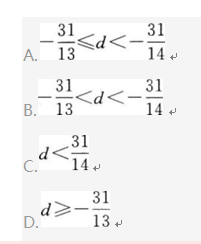


    答案：A
    解析：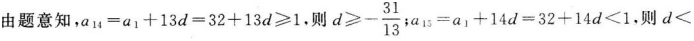

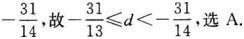
  • 第22题：

    关于倒年系数法的理解与应用说法正确的有（）

    • A、折旧系数是等差数列，但折旧额不一定
    • B、折旧系数与折旧额都是等差数列
    • C、折旧系数总和等于1
    • D、折旧额总和等于原设备购入价减去残值

    正确答案:B,C

  • 第23题：

    单选题
    在等差数列{an}中，已知前15项之和S15＝90，那么a8＝（　　）．
    A

    3

    B

    4

    C

    6

    D

    12


    正确答案： A
    解析：
    根据等差数列性质有S15＝15a8＝90，解得a8＝6．

相关内容