函数(x)=x2+2(m-1)x+2在区间(-∞,4)上是减函数,则实数m的取值范围是( )A.m≥-3 B.m=-3 C.m≤-3 D.m≥3
题目
B.m=-3
C.m≤-3
D.m≥3
相似考题
更多“函数(x)=x2+2(m-1)x+2在区间(-∞,4)上是减函数,则实数m的取值范围是( )A.m≥-3 B.m=-3 C.m≤-3 D.m≥3”相关问题
-
第1题:
下列哪项属于胆碱能受体
A.M、α
B.M、β
C.M、α
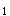 和β
和β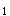
D.M、α
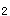 、β
、β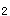
E.M、N
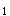 和N
和N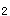 正确答案:E
正确答案:E
-
第2题:
二维数组M[i,j]的元素是4个字符(每个字符占一个存储单元)组成的串,行下标i范围从0~4,列下标j的范围从0~5。M按行存储时元素H[3,5]的起始地址与M按列存储时元素______的起始地址相同。
A.M[2,4]
B.M[3,4]
C.M[3,5]
D.M[4,4]
正确答案:B
解析:按行存储时M[3,5]的存储位置为:683+5=23,若按列存储,则与其地址相同的元素为M[3,4]:4*5+3=23。 -
第3题:
● 在13个元素构成的有序表M[1..13]中进行折半查找(向下取整),若找到的元素为M[4],则被比较的元素依次为(59)。 A.M[7]、 M[3]、M[5]、M[4] B.M[7]、M[5]、M[4] C.M[7]、M[6]、M[4] D.M[7]、M[4]
正确答案:A
试题59分析整个查找的过程为:(1+13)/2=7,因此首先与第7元素比较,由于要查找的元素在其前面,因此用(1+7-1)/2=3,然后与第3个元素比较,由于待查找在其后面,因此用(3+1+6)/2=5,因此接下来与第5个元素进行比较,最后再与第4个元素比较,找到了M[4]。参考答案(59)A -
第4题:
_____
A.M[15]
B.M[20]
C.M[35]
D.M[39]
正确答案:C
-
第5题:
已知函数f(x)是定义在R上的奇函数,若f(x)的最小正周期为4,且f(1)>0,f(3)=
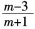
则m的取值范围是( )。A.-3<m<1
B.m>1或m<-3
C.-1<m<3
D.m>3或m<-1答案:C解析:
-
第6题:
已知函数f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,则该函数在 [-2,2]上的最小值是:A. 3
B. -5
C. -40
D. -37答案:D解析:提示:已知最大值为3,经以下计算得m=3。
f(x)=6x2 -12x = 6x(x-2),令f'(x)= 0,得 x1=0,x2= 2
f"(x)= 12x -12,f"(0) =-120,所以在x = 0 取得极大值代入f(x),f极大(0)= 0-0 + m = 3,m = 3
端点x = 2,x =-2 比较f(0)、f(2)、f(-2)函数值大小,得:fmin(-2)=-37 -
第7题:
若函数y=f(z)在[a,b]上单调,则使得y=f(x+3)必为单调函数的区间是( )A.[a,b+3]
B.[a+3,b+3]
C.[a一3,b—3]
D.[a+3,b]答案:C解析: -
第8题:
下列函数中,既是偶函数,又在区间(0,3)为减函数的是()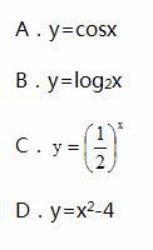 答案:A解析:
答案:A解析: -
第9题:
在一个请求页式存储管理中,一个程序的页面表向为4、3、2、1、4、3、5在该访问中发生的缺页次数F和缺页率f是()。A.M=4,F=8,f≈67%
B.M=4,F=5,f≈42%
C.M=3,F=9,f≈75%
D.M=3,F=1O,f≈83%答案:A,D解析:
-
第10题:
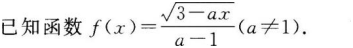
(1)若a>0,则?(x)的定义域是__________;
(2)若?(x)在区间(0,1]上是减函数,则实数a的取值范围是__________.答案:解析: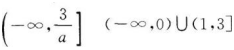
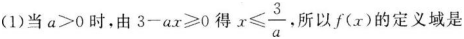

-
第11题:
若反比例函数的表达式为y=3/x,则当x<-1时,y的取值范围是-3<y<0。
正确答案:正确 -
第12题:
判断题若反比例函数的表达式为y=3/x,则当x<-1时,y的取值范围是-3<y<0。A对
B错
正确答案: 对解析: 暂无解析 -
第13题:
二维数组M[i,]的元素是4个字符(每个字符占一个存储单元)组成的串,行下标i的范围从0到4,列下标j的范围从0到5。M按行存储时元素M[3,5]的起始地址与M按列存储时元素(43)的起始地址相同。
A.M[2,4]
B.M[3,4]
C.M[3,5]
D.M[4,4]
正确答案:B
解析:当按行存储的时候,M[3,5]的起始地址为(3*6+6)*4=96。当按列存储的时候,M[3,4]的起始地址为(4*5+4)*4=96。所以应该选择B。 -
第14题:
若有定义语句:int m[]={5,4,3,2,1},i=4;,则下面对m数组元素的引用中错误的是______。
A.m[-i]
B.m[2*2]
C.m[m[0]]
D.m[m[i]]
正确答案:C
解析:一维数组的定义方式为:类型说明符 数组名[常量表达式]。其中“常量表达式”表示元素的个数,即数组长度。元素的下标从0开始,最大下标是元素个数减一。本题定义了一个由5个元素(m[0[到m[4])组成的数组。选项A表示对m[3]的引用;选项B表示对m[4]的引用;由于m[0]的值为5,所以选项C表示m[5],但由于m数组元素的最大下标为4,所以本引用下标越界;由于m[i]即m[4]的值为1,所以选项D表示对m[1]的引用。 -
第15题:
下列函数中,既是偶函数,又在区间(0,3)上为减函数的是 ( )

A.A
B.B
C.C
D.D
正确答案:A
本题主要考查的知识点为偶函数和减函数的性质.【应试指导】易知,A、C项为偶函数,B、D项为非奇非偶函数.在区间(0,3)上,C项中的函数为增函数,而A项中y=COSx的减区间为(2kπ,2kπ+π),故y=COSx在(0,3)上为减函数. -
第16题:
二维数组M[i,j]的元素是4个字符(每个字符占一个存储单元)组成的串,行下标i范围从0到4,列下标,i的范围从0到5。M按行存储时元素M[3,5]的起始地址与M按列存储时元素( )的起始地址相同。
A.M[2,4)
B.M[3,4)
C.M[3,5]
D.M[4,4)
正确答案:B
解析:M按行存储时元素M[3,5]位于第4行第6列(下标从0开始),也就是处在第3×6+6=24个存储位置,设与它存储的起始位置相同的,按列存储时的元素行下标为x,列下标为y,则有y×5+x+1=24,解得x=3,y=4,即选项B是正确答案。 -
第17题:
已知集合A={x|x2-3x-4>0},集合B={x|m+1≤x≤4m},若B?A,则实数m的取值范围为()。A.(-∞,3)
B.(-(1/4),3)
C.(-∞,-(1/4))∪(3,+∞)
D.(-∞,1/3)∪(3,+∞)答案:D解析: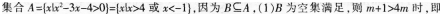

-
第18题:
二次函数y=2x2+mx-5在区间(-∞,-1)内是减函数,在区间(-1,+∞)内是增函数,则m的值是( )A.4
B.-4
C.2
D.-2答案:A解析: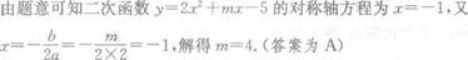
-
第19题:
不等式2x2+3mx+2m>0的解集是实数集,则m的取值范围是( )
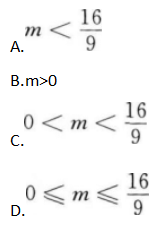 答案:C解析:【考情点拨】本题主要考查的知识点为不等式的解集. 【应试指导】由2x2+3mx+2m>0的解集为R,又因为抛物线的开口向上,所以方程2x2+3mx+2m=0无实根,
答案:C解析:【考情点拨】本题主要考查的知识点为不等式的解集. 【应试指导】由2x2+3mx+2m>0的解集为R,又因为抛物线的开口向上,所以方程2x2+3mx+2m=0无实根,
-
第20题:
函数(x)=x3-6x2+9x在区间[-3,3]上的最大值为___.答案:解析:【答案】4 【考情点拨】本题主要考查的知识点为函数的最值.
【应试指导】此题是高次函数的最值问题,可用导数来求函数在区间[-3,3]上的最值.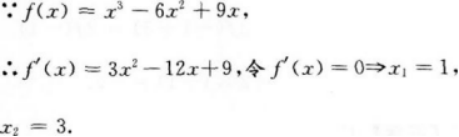
列出表格
由上表可知函数在[-3,3]上,在x=1点处有最大值4. -
第21题:
函数y=x2-2x在区间[2,3]上的最大值是( )。A.0
B.3
C.4
D.5答案:B解析:函数的开口向上,对称轴为x=1,可知函数在区间[2,3]上单调递增,在此区间上的最大值在x=3处取得,为3,选择B。 -
第22题:
已知集合A={x∣x2-3x-4>0},集合B={x∣m+1≤x≤4m),若B∈A,则实数m的取值范围为( )。
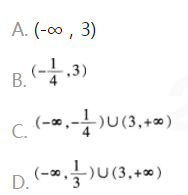 答案:D解析:
答案:D解析:
-
第23题:
已知函数f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,则该函数在[-2,2]上的最小值是()
- A、3
- B、-5
- C、-40
- D、-37
正确答案:D
