itgle.com

抛物线y2＝4x上一点P到焦点F的距离是10，则点P坐标是（　　）A.(9，6) B.(9，±6) C.(6，9) D.(±6，9)

题目
抛物线y2＝4x上一点P到焦点F的距离是10，则点P坐标是（　　）

A.(9，6)
B.(9，±6)
C.(6，9)
D.(±6，9)
相似考题

1.（3）①小丽同学发现：“当点P运动到OH上时，点P到l的距离最小．”事实上，还存在着点P到l距离最大的位置，此时，点P到l的距离是_____________分米；

2.已知过点（0，4），斜率为-1的直线l与抛物线C：y2—2px（b&gt；0）交于A，B两点．（I）求C的顶点到2的距离；（Ⅱ）若线段AB中点的横坐标为6，求C的焦点坐标．

3.下面程序的输出结果是()。include using namespace std;class point {public:point(in下面程序的输出结果是( )。 #include ＜iostream＞ using namespace std; class point { public: point(int px=10,int py=10){ x=px;y=py;} getpx( ) { return x;} getpy( ) { return y;} private: int x,y; }; void main(voiD) { point p,q(15,15); cout＜＜"p点的坐标是:"＜＜p. getpx( )＜＜" ,"; cout＜＜p. getpy( )＜＜endl; cout＜＜"q点的坐标是:"＜＜q. getpx( )＜＜" ,"; cout＜＜q. getpy( ); }A．p点的坐标是:10,10 q点的坐标是:15,15B．p点的坐标是:0,0 q点的坐标是:15,15C．p点的坐标是:0,0 q点的坐标是:0,0D．p点的坐标是:10,10 q点的坐标是:10,10

4.A，B是抛物线Y 2—8x上两点，且此抛物线的焦点段AB上，已知A，B两点的横坐标之和为l0，则 （ ）A.18B.14C.12D.10

更多“抛物线y2＝4x上一点P到焦点F的距离是10，则点P坐标是（　　）”相关问题

  • 第1题：

    已知A,B是抛物线y2=4x上的两个动点,且|AB|=3,则当AB的中点M到y轴的距离最短时,点M的横坐标是____.


    参考答案B9/16

  • 第2题：

    过抛物线y2=4x的焦点，作直线与此抛物线相交于两点P和Q，那么线段PQ中点的轨迹方程是（　　）．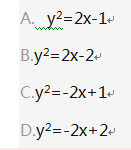


    答案：B
    解析：
    (筛选法)由已知可知轨迹曲线经过点(1，0)，开口向右，由此排除答案A、C、D，所以选B.

  • 第3题：

    设直线y=2x+m与抛物线y2=4x没有公共点，则m的取值范围是。


    答案：
    解析：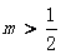

  • 第4题：

    抛物线x2=-16y上一点P到焦点的距离是6，则点P的坐标是( )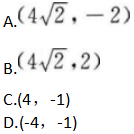


    答案：A
    解析：
    【考情点拨】本题主要考查的知识点为抛物线的定义． 【应试指导】本题应从抛物线的定义去考虑．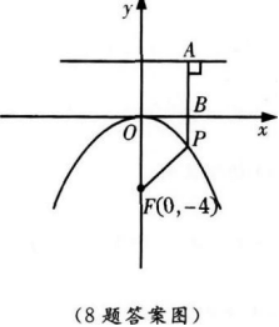


    ∴F(0，-4)，
    ∴准线方程y=4，由题意得｜PF｜=6，
    ∴｜PA｜=6，
    ∵｜AB｜=4，
    ∴｜PB｜=2，
    ∴P点的坐标为(x，-2)，
    ∵P(x，-2)点在抛物线上，
    ∴x2=-16×(-2)=32．

  • 第5题：

    已知M是抛物线y2=2px(p>0)上的点，F是抛物线的焦点，∠FOM=45o，|MF|=2。
    (1)求抛物线的方程式；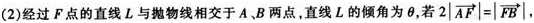




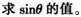
    答案：
    解析：


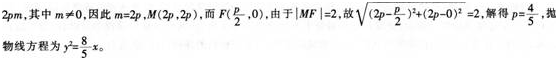
  • 第6题：

    设抛物线y2=2px(p>0)焦点为F，点A坐标为(0，2)，若线段FA的中点B在抛物线上，则B到该抛物线准线距离为__________。


    答案：
    解析：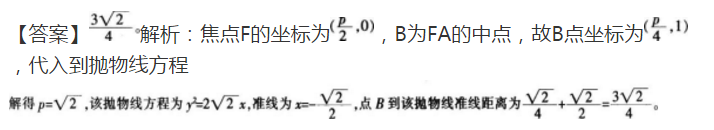

  • 第7题：

    极坐标法放样P点的步骤是：将仪器安置在已知点A上，对中整平后，后视另一已知点B，并以B点为零方向，放样AB与AP的夹角β，得AP方向，沿AP方向放样（）距离，得P点。

    • A、B到P的长度
    • B、A到B的长度
    • C、P到B的长度
    • D、A到P的长度

    正确答案:D

  • 第8题：

    方程 y2 = 2px（p＞0）是抛物线标准方程（SIEMENS系统）。


    正确答案:正确

  • 第9题：

    设C为抛物线y2=x上从点0（0，0）到点P（1，1）的一段弧，则曲线积分的值是（）．

    • A、2
    • B、1/2
    • C、1/3
    • D、1/4

    正确答案:C

  • 第10题：

    填空题
    已知点O到直线l上一点P的距离为3cm，圆O的半径为3cm，则直线l与圆的位置关系是____．

    正确答案： 相切或相交
    解析： 暂无解析

  • 第11题：

    单选题
    设C为抛物线y2=x上从点0（0，0）到点P（1，1）的一段弧，则曲线积分的值是（）．
    A

    2

    B

    1/2

    C

    1/3

    D

    1/4


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    过抛物线y＝4x的焦点，作直线与此抛物线相交于两点P和Q，那么线段PQ中点的轨迹方程（）
    A

    y＝2x－1

    B

    y＝2x－2

    C

    y＝－2x＋1

    D

    －2x＋2


    正确答案： B
    解析： 暂无解析

  • 第13题：

    如图所示，已知A，B为直线L：y=mx-m+2与抛物线y=x2的两个交点。
    (1)直线ι经过一个定点C，试求出点C的坐标；(2分)
    (2)若m=-1，已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合)，且△ABP的面积为（3√13）/2，求点P的坐标。(6分)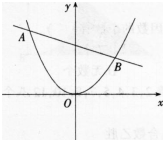


    答案：
    解析：
    (1)直线L：y=m(x-1)+2，当x=1时，y的取值与m无关，此时y=2，所以直线过定点(1，2)；

  • 第14题：

    已知动点P在曲线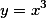上运动，记坐标原点与点P间的距离为l.若点P的横坐标对时间的变化率为常数,则当点P运动到点(1,1)时，l对时间的变化率是


    答案：
    解析：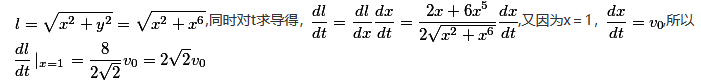

  • 第15题：

    A．B是抛物线y2=8x上两点，且此抛物线的焦点在线段AB上，已知A．B两点的横坐标之和为10，则|AB|=（　　）

    A.18
    B.14
    C.12
    D.10

    答案：B
    解析：

  • 第16题：

    设P是圆x2+y2=2上的一点，该圆在点P的切线平行于直线x+y+2=0，则点P的坐标为



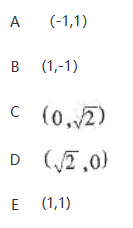    答案：E
    解析：

  • 第17题：

    已知P为抛物线y2=x的焦点，点M，N在该抛物线上且位于x轴的两侧，

    (其中O为坐标原点)，则ΔMPO与ΔNPO面积之和的最小值是( )。


    答案：B
    解析：
    设直线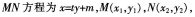

    直线方程与抛物线方程联立，可得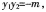


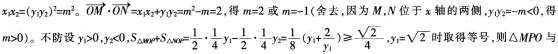
    △NPO面积之和的最小值是

  • 第18题：

    过抛物线y2=4x的焦点，倾斜角为45°的直线方程为_______。


    答案：
    解析：
    【答案】x-y-1=0。解析：抛物线y2=4x的焦点为(1，0)，倾斜角为45°的直线斜率为1，则直线方程为x-y-1=0。

  • 第19题：

    设空间有一点p，则p到平面（n，d）的最短距离为（）

    • A、n.p+d
    • B、d
    • C、n.p
    • D、无法计算

    正确答案:A

  • 第20题：

    有一点实体，其矢量坐标为P（9.5，15.6），若网格的宽与高都是2，则P点栅格化的行列坐标为（）。

    • A、P（5，8）
    • B、P（8，5）
    • C、P（4，7）
    • D、P（7，4）

    正确答案:B

  • 第21题：

    单选题
    极坐标法放样P点的步骤是：将仪器安置在已知点A上，对中整平后，后视另一已知点B，并以B点为零方向，放样AB与AP的夹角β，得AP方向，沿AP方向放样（）距离，得P点。
    A

    B到P的长度

    B

    A到B的长度

    C

    P到B的长度

    D

    A到P的长度


    正确答案： D
    解析： 暂无解析

  • 第22题：

    填空题
    若直线ax－y＋1＝0经过抛物线y2＝4x的焦点，则实数a＝____．

    正确答案： -1
    解析：
    抛物线y2＝4x的焦点为（1，0），则a－0＋1＝0，得a＝－1．

  • 第23题：

    填空题
    已知点A（－1，1），B（3，5），x轴上一点M到A，B的距离相等，则点M的坐标是____．

    正确答案： (4,0)
    解析：
    设M（x，0），则得方程（x＋1）2＋12＝（x－3）2＋52，解此方程，得x＝4．

相关内容