itgle.com

对LP问题的标准型：maxZ=CX，AX=b，X≥0，利用单纯形表求解时，每做一次换基迭代，都能保证它相应的目标函数值Z必为（ ）A.增大 B.不减少 C.减少 D.不增大

题目
对LP问题的标准型：maxZ=CX，AX=b，X≥0，利用单纯形表求解时，每做一次换基迭代，都能保证它相应的目标函数值Z必为（ ）

A.增大
B.不减少
C.减少
D.不增大
相似考题

1.若x是原问题maxZ=CX,AX≤b,X≥0的可行解,y是其对偶问题MinS=Yb,YA≥C,Y≥0的可行解,则有()。A.CX≥YbB.CX≤YbC.CX=YbD.无法确定

2.对于线性规划标准型,利用单纯形求解时,每做一次换基迭代,都能保证其相应的目标函数值必为( )。A. 不增大B. 增大C. 减少D. 不减少

3.若LP最优解不唯一，则在最优单纯形表上()A、非基变量的检验数必有为0B、非基变量的检验数不必有为0者

4.对于线性规划问题标准型:maxZ=CX,AX=b,X≥0,利用单纯形法求解时,每作一次迭代,都能保证它相应的目标函数值Z必为()。A.增大B.不减少C.减少D.不增大

更多“对LP问题的标准型：maxZ=CX，AX=b，X≥0，利用单纯形表求解时，每做一次换基迭代，都能保证它相应的目标函数值Z必为（ ）”相关问题

  • 第1题：

    线性规划原问题（LP）为：

    对偶问题(Dp)为:

    现用单纯形法求解(LP)得最优解,则在最优单纯形表中,同时也可得到(DP)的最优等于()

    A、最优单纯形表中松弛变量的检验数;

    B、最优单纯形表中松弛变量的检验数的相反数

    C、最优单纯形表中非基变量的检验数

    D、最优单纯形表中非基变量的检验数的相反数


    答案：B

    解析：首先，原问题的松弛变量对应对偶问题的变量，对偶问题的剩余变量对应原问题的变量，故排除C和D，根据对偶理论，原问题与对偶问题是相互对偶的，有一定对应关系，故选B。

  • 第2题：

    对LP 问题的标准型:max ,,0Z CX AX b X ==≥,利用单纯形表求解时,每做一次换基迭代,都能保证它相应的目标函数值Z 必为( )

    A 增大

    B 不减少

    C 减少

    D 不增大


    参考答案B

  • 第3题：

    在单纯形表中进行迭代时，在b列中得到的是原问题的基可行解，在检验数行得到的是对偶问题的（）


    正确答案:基解

  • 第4题：

    单纯形法求解线性规划问题时，若要求得基础解，应当令（）

    • A、基变量全为0
    • B、非基变量全为0
    • C、基向量全为0
    • D、非基向量全为0

    正确答案:B

  • 第5题：

    互为对偶的两个线性规划maxZ=CX，AX≤b，X≥0及minW=Yb，YA≥C，Y≥0对任意可行解X和Y，存在关系（）

    • A、Z＞W
    • B、Z=W
    • C、Z≥W
    • D、Z≤W

    正确答案:D

  • 第6题：

    用单纯形法求解Max型的线性规划问题时，检验数Rj＞0对应的变量都可以被选作入基变量。


    正确答案:正确

  • 第7题：

    在单纯形表中进行迭代时，在b列中得到的是原问题的（），在检验数行得到的是对偶问题的基解。


    正确答案:基可行解

  • 第8题：

    填空题
    在单纯形表中进行迭代时，在b列中得到的是原问题的（），在检验数行得到的是对偶问题的基解。

    正确答案： 基可行解
    解析： 暂无解析

  • 第9题：

    填空题
    在单纯形表中进行迭代时，在b列中得到的是原问题的基可行解，在检验数行得到的是对偶问题的（）

    正确答案： 基解
    解析： 暂无解析

  • 第10题：

    单选题
    单纯形法求解线性规划问题时，若要求得基础解，应当令（）
    A

    基变量全为0

    B

    非基变量全为0

    C

    基向量全为0

    D

    非基向量全为0


    正确答案： B
    解析： 暂无解析

  • 第11题：

    判断题
    用单纯形法求解Max型的线性规划问题时，检验数Rj＞0对应的变量都可以被选作入基变量。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第12题：

    单选题
    过点（-1，0，1）且与平面x+y+4z+19=0平行的平面方程为（）。
    A

    x+y+4z-3=0

    B

    2x+y+z-3=0

    C

    x+2y+z-19=0

    D

    x+2y+4z-9=0


    正确答案： C
    解析： 暂无解析

  • 第13题：

    对于线性规划标准型,利用单纯形求解时,每做一次换基迭代,都能保证它相应的目标函数值必为不减少。()

    此题为判断题(对，错)。


    正确答案：√

  • 第14题：

    目标函数为maxZ=28x4+x5+2x6，约束形式为“≤”，且X1X2X3必为松弛变量，表中的解代入目标函数中得Z=12,求出a~g的值.并判断是否最优解。


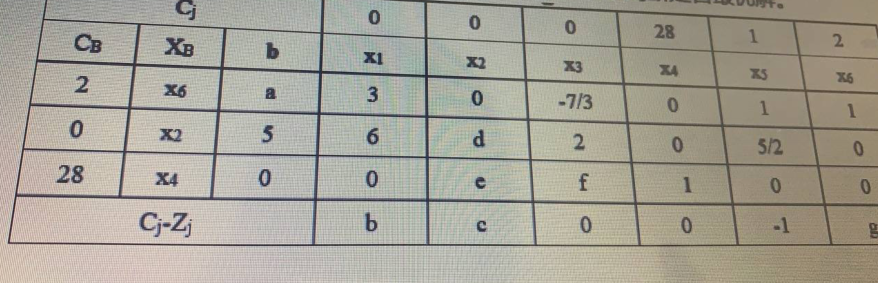    参考答案：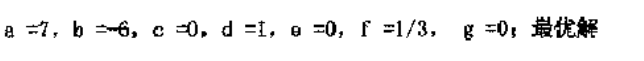

  • 第15题：

    下列关于线性规划叙述正确的是（）。

    • A、线性规划问题，若有最优解，则必是一个基变量组的可行基解
    • B、线性规划问题一定有可行基解
    • C、线性规划问题的最优解只能在最低点上达到
    • D、单纯型法求解线性规划问题时，每换基迭代一次必使目标函数值下降一次

    正确答案:A

  • 第16题：

    关于运输问题的说法不正确的是（）。

    • A、它可用线性规划的单纯形表求解
    • B、它可用表上作业法求解
    • C、它的约束方程数等于基变量的数目
    • D、它一定有最优解

    正确答案:C

  • 第17题：

    单纯形法中确定换出变量时，若一次迭代中有多个基变量为零，称出现了（）


    正确答案:退化解

  • 第18题：

    对LP问题标准型，利用单纯形法求解时，每做一次换基迭代，都能保证它相应的目标函数值Z必为（）

    • A、增大
    • B、不减少
    • C、减少
    • D、不增大

    正确答案:B

  • 第19题：

    问答题
    下表中给出线性规划问题计算过程中某次迭代的单纯形表，目标函数为： ，约束条件均为≤，表中x 4，x 5，x 6为松弛变量，表中目标函数值Z=14。 1 ）求出 a-g 的值； 2 ）表中给出的解是否为最优解。

    正确答案： （1）a=7，b=-6，c=0，d=1，e=0，f=1/3，g=0；
    （2）表中给出最优解X *＝（0  0  7  0  5  0） T。
    解析： 暂无解析

  • 第20题：

    单选题
    关于运输问题的说法不正确的是（）。
    A

    它可用线性规划的单纯形表求解

    B

    它可用表上作业法求解

    C

    它的约束方程数等于基变量的数目

    D

    它一定有最优解


    正确答案： D
    解析： 暂无解析

  • 第21题：

    单选题
    对LP问题标准型，利用单纯形法求解时，每做一次换基迭代，都能保证它相应的目标函数值Z必为（）
    A

    增大

    B

    不减少

    C

    减少

    D

    不增大


    正确答案： D
    解析： 暂无解析

  • 第22题：

    单选题
    下列关于线性规划叙述正确的是（）。
    A

    线性规划问题，若有最优解，则必是一个基变量组的可行基解

    B

    线性规划问题一定有可行基解

    C

    线性规划问题的最优解只能在最低点上达到

    D

    单纯型法求解线性规划问题时，每换基迭代一次必使目标函数值下降一次


    正确答案： D
    解析： 暂无解析

  • 第23题：

    单选题
    互为对偶的两个线性规划maxZ=CX，AX≤b，X≥0及minW=Yb，YA≥C，Y≥0对任意可行解X和Y，存在关系（）
    A

    Z＞W

    B

    Z=W

    C

    Z≥W

    D

    Z≤W


    正确答案： A
    解析： 暂无解析

相关内容