itgle.com

当非正弦函数f（t）满足狄里赫利条件时，可将其展开成傅里叶级数。（ ）

题目
当非正弦函数f（t）满足狄里赫利条件时，可将其展开成傅里叶级数。（ ）

相似考题

1.已知f(t)是周期为T的函数,f(t)－f(t＋2.5T)的傅里叶级数中,不可能有________。;A.正弦分量B.余弦分量C.奇次谐波分量D.偶次谐波分量

2.非正弦周期信号的分解可用什么方法实现：（）A.傅里叶变化；B.傅里叶变换；C.傅里叶级数展开；D.傅里叶卷积

3.大多数非正弦周期函数的傅里叶级数都已被算出。()

4.偶函数的傅里叶级数展开式中包括()和()。

更多“当非正弦函数f（t）满足狄里赫利条件时，可将其展开成傅里叶级数。（ ）”相关问题

  • 第1题：

    非正弦周期电流电路稳态分析有2个步骤展开成傅里叶级数和叠加出最后结果。（）


    正确答案:错误

  • 第2题：

    傅里叶级数展开中,包含正弦分量,则原信号必为奇函数。()

    此题为判断题(对，错)。


    参考答案：错误

  • 第3题：

    满足狄里赫利收敛条件时,傅氏级数与原周期信号f(t)之间下列哪些说法不正确()。

    A、处处相等

    B、只能保证傅氏级数系数有界

    C、除f(t)不连续的t值外，处处相等

    D、处处不相等，但能量相同


    参考答案：ABD

  • 第4题：

    周期信号f(t)=－f(t±T／2),(T—周期),下列哪些不是其傅里叶级数展开式的结构特点()。

    A、只有正弦项

    B、只有余弦项

    C、只含偶次谐波

    D、只含奇次谐波


    参考答案：BCD

  • 第5题：

    下列命题中，错误的是( ).

    A.设f(x)为奇函数，则f(x)的傅里叶级数是正弦级数
    B.设f(x)为偶函数，则f(x)的傅里叶级数是余弦级数
    C.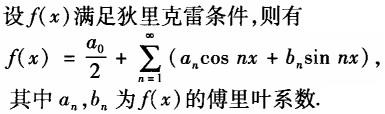
    D.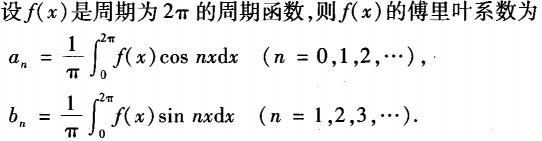

    答案：C
    解析：

  • 第6题：



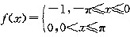
    展开成傅里叶级数时，该级数在x=0处的值为( )。



    答案：B
    解析：
    x=0是f(x)的第一类间断点，根据收敛定理，级数在点x=0处收敛于

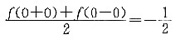
  • 第7题：

    傅里叶级数是傅里叶在研究（）现象时提出的


    正确答案:热传导

  • 第8题：

    Acos（√31t）的傅里叶三角函数形式级数中的正弦分量幅值bn=（）


    正确答案:0

  • 第9题：

    若f（t）是周期奇函数，则其傅氏级数中仅含有正弦分量。


    正确答案:正确

  • 第10题：

    填空题
    Acos（√31t）的傅里叶三角函数形式级数中的正弦分量幅值bn=（）

    正确答案： 0
    解析： 暂无解析

  • 第11题：

    单选题
    周期为丁的非正弦信号可以分解为傅里叶级数的条件为（）。
    A

    满足狄利赫利条件

    B

    无条件

    C

    必须平均值为零


    正确答案： A
    解析： 暂无解析

  • 第12题：

    填空题
    复杂的周期信号可借助傅里叶级数展开成（），其中任两个分量的频率比都是有理数.

    正确答案： 一系列的离散的简谐分量之和
    解析： 暂无解析

  • 第13题：

    满足狄里赫利收敛条件时,傅氏级数与原周期信号f(t)之间________。

    A.处处相等

    B.只能保证傅氏级数系数有界

    C.除f(t)不连续的t值外，处处相等

    D.处处不相等，但能量相同


    正确答案：C

  • 第14题：

    狄里赫利条件是().

    A、周期非正弦函数在一个周期内只有有限个第一类不连续点

    B、周期非正弦函数在一个周期内只有有限个极大值

    C、周期非正弦函数在一个周期内只有有限个极小值

    D、在周期T内绝对可积


    参考答案：ABCD

  • 第15题：

    已知f(t)是周期为T的函数,f(t)－f(t＋(5／2)T)的傅里叶级数中,不可能的是()。

    A、正弦分量

    B、余弦分量

    C、奇次谐波分量

    D、偶次谐波分量


    参考答案：ABD

  • 第16题：

    若周期信号f(t)是时间t的奇函数,则其三角形傅里叶级数展开式中()。

    A.没有余弦分量

    B.既有正弦分量和余弦分量，又有直流分量

    C.既有正弦分量和余弦分量

    D.仅有正弦分量


    正确答案：D

  • 第17题：

    设f(x)是周期为2π的周期函数，它在[-π，π]上的表达式为：


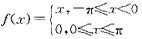
    若将f(x)展开成傅里叶级数，则该级数在x=-3π处收敛于( )。



    答案：C
    解析：
    所给函数满足收敛定理，当x=-3π为函数的问断点，函数f(x)的傅里叶级数在x

  • 第18题：

    下列( )是周期为T的非正弦信号可以分解为傅里叶级数的条件。

    A.满足狄利赫利条件
    B.频谱是连续的
    C.必须平均值为零
    D.频谱是断续的

    答案：A
    解析：
    周期为T的非正弦信号可以分解为傅里叶级数的条件是满足狄利赫利条件。

  • 第19题：

    Asin（√31t）的傅里叶三角函数形式级数中的余弦an=（）


    正确答案:0

  • 第20题：

    周期为丁的非正弦信号可以分解为傅里叶级数的条件为（）。

    • A、满足狄利赫利条件
    • B、无条件
    • C、必须平均值为零

    正确答案:A

  • 第21题：

    复杂的周期信号可借助傅里叶级数展开成（），其中任两个分量的频率比都是有理数.


    正确答案:一系列的离散的简谐分量之和

  • 第22题：

    单选题
    如下不正确的描述是（）。
    A

    满足狄里赫利条件的周期信号可描述为傅里叶级数形式

    B

    满足狄里赫利条件的周期信号可分解为一系列谐波分量

    C

    满足狄里赫利条件的周期信号的频谱是离散的频谱

    D

    满足狄里赫利条件的周期信号的谱线密度与周期信号的周期无关


    正确答案： D
    解析： 暂无解析

  • 第23题：

    填空题
    Asin（√31t）的傅里叶三角函数形式级数中的余弦an=（）

    正确答案： 0
    解析： 暂无解析

相关内容