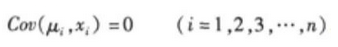itgle.com

在简单线性回归分析中，关于误差项随机变量的理论假设包括( )。A、服从正态分布B、数学期望等于0C、相互独立D、方差相等

题目

在简单线性回归分析中，关于误差项随机变量的理论假设包括( )。

A、服从正态分布

B、数学期望等于0

C、相互独立

D、方差相等

相似考题

1.线性回归的基本假设不包括哪个()A.随机误差项是一个期望值为0的随机变量B.对于解释变量的所有观测值，随机误差项有相同的方差C.随机误差项彼此相关D.解释变量是确定性变量不是随机变量，与随机误差项之间相互独立E.随机误差项服从正态分布

2.回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型中关于随机项μi的基本假设是（ ）。 Ⅰ.随机项μi自变量的任一观察值xi不相关 Ⅱ.E（μi）=0，V（μi）=σμ^2=常数 Ⅲ.线每个μi为独立同分布，服从正态分布的随机变量 Ⅳ.各个随机误差项之间不相关A.Ⅰ.Ⅱ.Ⅲ B.Ⅰ.Ⅱ.Ⅲ.Ⅳ C.Ⅱ.Ⅲ.Ⅳ D.Ⅰ.Ⅲ.Ⅳ

3.回归分析是期货投资分析中重要的统计分析方法,而线性回归模型是回归分析的基础。线性回归模型的基本假设是（ ） Ⅰ.被解释变量与解释变量之间具有线性关系 Ⅱ.随机误差项服从正态分布 Ⅲ.各个随机误差项的方差相同 Ⅳ.各个随机误差项之间不相关A.Ⅰ.Ⅱ.Ⅲ.Ⅳ B.Ⅰ.Ⅲ.Ⅳ C.Ⅰ.Ⅱ.Ⅳ D.Ⅱ.Ⅲ.Ⅳ

4.对于简单线性回归模型的假设条件，下列哪一种说法不正确（）A.误差项是一个独立的随机变量B.误差项的期望值等于0C.误差项的方差可以不同D.误差项为正太分布

更多“在简单线性回归分析中,关于误差项随机变量的理论假设包括( )。A、服从正态分布B、数学期望等于0C ”相关问题

  • 第1题：

    回归分析是期货投资分析中重要的统计分析方法,而线性回归模型是回归分析的基础。线性回归模型的基本假设是（ ）
    Ⅰ.被解释变量与解释变量之间具有线性关系
    Ⅱ.随机误差项服从正态分布
    Ⅲ.各个随机误差项的方差相同
    Ⅳ.各个随机误差项之间不相关

    A：Ⅰ.Ⅱ.Ⅲ.Ⅳ
    B：Ⅰ.Ⅲ.Ⅳ
    C：Ⅰ.Ⅱ.Ⅳ
    D：Ⅱ.Ⅲ.Ⅳ

    答案：A
    解析：
    —元线性回归模型为：yi=a+βi+mi（i=l,2,3,*,n）,其中yi为解解释变量Xi为解释变量;ui是一个随机变垦量.称为随机项。要求随机项u和自变量，Xi满足的统计假定如下：①每个ui均为独立同分右（IID、）,服从正态分右的随机变量，E（ui）=0,V（ui）=σ＾2常数②随机项ui与自变量的任一观察值Xi不相关，即COV（ui,i）=0

  • 第2题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型的基本假设是（）。
    Ⅰ被解释变量与解释变量之间具有线性关系
    Ⅱ随机误差项服从正态分布
    Ⅲ各个随机误差项的方差相同
    Ⅳ各个随机误差项之间不相关

    A.Ⅰ、Ⅱ、Ⅲ
    B.Ⅰ、Ⅲ、Ⅳ
    C.Ⅱ、Ⅲ、Ⅳ
    D.Ⅰ、Ⅱ、Ⅲ、Ⅳ

    答案：D
    解析：
    一元线性回归模型为：yi=α+βxi+ui,（i=1,2,3,…,n），其中yi为被解释变量；xi为解释变量，ui是一个随机变量，称为随机项。要求随机项ui和自变量xi满足的统计假定如下：①每个ui均为独立同分布，服从正态分布的随机变量，且E（ui）=0，V（ui）=σ2=常数；②随机项ui与自变量的任一观察值xi不相关，即Cov（ui，xi）=0。

  • 第3题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型中关于随机项i的基本假设是（ ）。
    Ⅰ.随机项i与自变量的任一观察值Xi不相关
    Ⅱ. E(i)=0,V(i)=σ2=常数
    Ⅲ.每个i均为独立同分布，服从正态分布的随机变量
    Ⅳ.各个随机误差项之间不相关

    A、Ⅰ.Ⅱ.Ⅲ
    B、Ⅰ.Ⅱ.Ⅲ.Ⅳ
    C、Ⅱ.Ⅲ.Ⅳ
    D、Ⅰ.Ⅱ.Ⅳ


    答案：B
    解析：

  • 第4题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型的基本假设是（ ）。
    Ⅰ.被解释变量与解释变量之间具有线性关系
    Ⅱ.随机误差项服从正态分布
    Ⅲ.各个随机误差项的方差相同
    Ⅳ.各个随机误差项之间不相关

    A、Ⅰ.Ⅱ.Ⅲ
    B、Ⅰ.Ⅱ.Ⅳ
    C、Ⅱ.Ⅲ.Ⅳ
    D、Ⅰ.Ⅱ.Ⅲ.Ⅳ


    答案：D
    解析：
    一元线性回归模型为:yi=α+βxi+ui,(i=1,2,3,…,n)，其中yi为解释变量;xi为解释变量；ui是一个随机变量，称为随机项。要求随机项ui和自变量xi满足的统计假定如下:①每个A均为独立同分布(IID),服从正态分布的随机变量，且E(ui)=0, V(ui)=σ2=常数；②随机项ui与自变量的任一观察值xi不相关，即COV (ui,xi)=0。

  • 第5题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型早回归分析的基础。线性回归模型中关于随机项μi的基本假设是（ ）。
    Ⅰ.随机项μi与自变量的任一观察值xi不相关=常数
    Ⅱ.
    Ⅲ.每个μi均为独立同分布，服从正态分布的随机变量
    Ⅳ.各个随机误差项之间不相关

    A、Ⅰ.Ⅱ.Ⅲ.Ⅳ
    B、Ⅰ.Ⅱ.Ⅲ
    C、Ⅰ.Ⅱ.Ⅳ
    D、Ⅱ.Ⅲ.Ⅳ


    答案：A
    解析：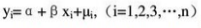
    一元线性回归模型为:，其中yi为被解释变量；xi为解释变量；μi是一个随机变量，称为随机项。随机项μi满足如下基本假定:①每个μi均为独立同分布，服从正态分布的随机变量，且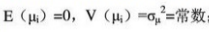；②每个随机相Ri均互不相关，即；③随机项Ri与自变量的任一观察值xi不相关,即:


相关内容