itgle.com

某城市某类房地产1998~2006年的价格见表2—24。试利用最小二乘法拟合一直线趋势方程，并用该方程预测该类房地产2007年和2008年的价格。因此，描述该类房地产价格变动长期趋势线的方程为： Y =a+6X =3 522. 22 + 528. 33X 根据该方程计算的1998~2006年该类房地产价格的趋势值。 预测该类房地产2007年的价格为： Y =3 522. 22 + 528. 33X =(3 522. 22 + 528. 33X6)元/m2 =6 692. 2 元/m2 预测该类房地产200

题目
某城市某类房地产1998~2006年的价格见表2—24。试利用最小二乘法拟合一直线趋势方程，并用该方程预测该类房地产2007年和2008年的价格。


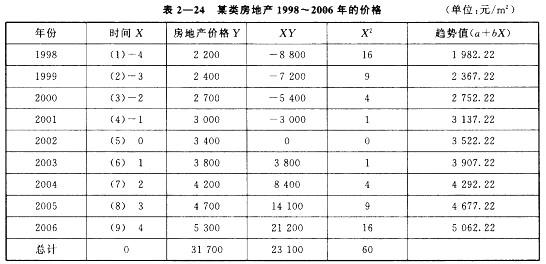
因此，描述该类房地产价格变动长期趋势线的方程为：
Y =a+6X
=3 522. 22 + 528. 33X 根据该方程计算的1998~2006年该类房地产价格的趋势值。
预测该类房地产2007年的价格为：
Y =3 522. 22 + 528. 33X
=(3 522. 22 + 528. 33X6)元/m2 =6 692. 2 元/m2 预测该类房地产2008年的价格为：
Y =3 522. 22 + 528. 33X
=(3 522. 22 + 528. 33X7)元/m2
=7 220. 53 元/m 2

相似考题

1.某地区某类房地产J999～2005年价格如下表所示：某类房地产1999～2005年价格 单位:元/m2 年份 1999 2000 2001 2002 2003 2004 2005 2006 房地产价格 1800 2000 2100 2300 2500 2800 3000 根据直线趋势法，预测该地区该类型房地产2006年的价格为（ ）元/m2。A．3300B．3157C．3357D．3156

2.假定被研究现象基本上是按不变的发展速度发展,为描述现象变动的趋势,借以进行预测,应拟合的方程为( )。A. 直线趋势方程B. 指数曲线方程C. 双曲线方程D. 直线或曲线方程均可

3.用最小二乘法拟合时间序列的直线趋势方程Y=a＋bt时,若0≤b≤1则该时间 序列的趋势为逐步上升的趋()此题为判断题(对，错)。

4.某地区某类房地产1999-2005年价格如下表所示：某类房地产1999-2005年价格 单位：元/m2 年份 1999 2000 2001 2002 2003 2004 2005 2006 房地产价格 1800 2000 2220 2460 2730 3030 3360 ？根据平均发展速度法进行估价，预测该地区该类型房地产2006年的价格为（ ）元/m2。A．3700B．3785C．3729D．3156

参考答案和解析
答案：
解析：
改错如下：
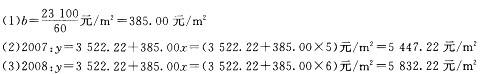
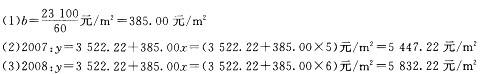
更多“某城市某类房地产1998~2006年的价格见表2—24。试利用最小二乘法拟合一直线趋势方程，并用该方程预测该类房地产2007年和2008年的价格。 ”相关问题

  • 第1题：

    假定被研究现象基本上按不变的发展速度发展,为描述现象变动的趋势,借以进行预测,应拟合()。

    A.直线趋势方程

    B.直线或曲线方程均可

    C.指数曲线方程

    D.二次曲线方程


    正确答案：C

  • 第2题：

    用最小二乘法拟合回归直线方程，其基本原理是（ ）。


    正确答案：D

  • 第3题：

    需要预测某宗房地产2007年、2008年的价格。通过市场调研，获得该类房地产2002~2006年的价格并计算其逐年上涨额见表2—9。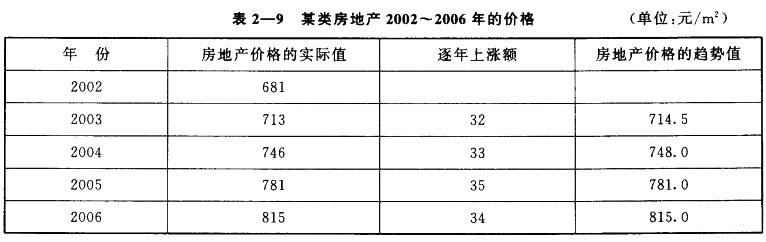

    预测该宗房地产2007年的价格为（ ）元/m2。
    A.841.0 B.846.0 C.848.5 D.851.0


    答案：C
    解析：

  • 第4题：

    根据最小二乘法拟合直线回归方程是使（ ）。



    答案：A
    解析：
    最小二乘法就是使得因变量的观测值yi与估计值之间的离差平方和最小来估计参数β0和β1的方法。

  • 第5题：

    某类房地产2012～2016年的价格见下表，根据平均发展速度，预测该类房地产2017年的价格为（　）元/m2。
    某类房地产2012～2016年的价格


    A、10300
    B、10400
    C、11140
    D、11265

    答案：C
    解析：
    本题考查的是平均发展速度法。平均发展速度＝（9000/3800） 1/4＝1.24
    2011年价格＝3800×1.24 5＝11140
    参见教材P389。

  • 第6题：

    某类房地产2006—2010年的价格见表1，根据平均发展速度法，预测该类房地产2011年的价格为（　　）元/m2。
    表1　某类房地产2006—2010年的价格

    A．10300
    B．10400
    C．11165
    D．11265

    答案：C
    解析：

    2011年该房地产价格V5=P0?ti=3800×1.240555=11165（元/m2）。

  • 第7题：

    某类房地产的历史价格变动时高时低，但总体上呈上升趋势，现在要预测该类房地产的未来价格，应该选用的预测方法是（　）。

    A.平均发展速度法
    B.平均增减量法
    C.数学曲线拟合法
    D.中位数法

    答案：C
    解析：
    本题考查的是数学曲线拟合法的公式。时高时低，不是平稳的数列，用平均发展速度和平均增减量法误差大，总体趋势上升，因而可以拟合数学趋势线。

  • 第8题：

    利用直线趋势法对某类商品住宅2004～2013年的平均价格进行分析，拟合成一直线趋势方程Y＝3522＋385X，其中Y为商品住宅价格，X为时间，且ΣX＝0。经验证该方程拟合度较高，则利用该方程预测该类商品住宅2014年的平均价格为（　　）元/㎡。

    A．5447
    B．5832
    C．6987
    D．7757

    答案：B
    解析：
    由题意，由于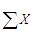
    =0，所以取2008年对应的X=-1，2009年对应的X=1，则2014年对应的X=6；该方程预测该类商品住宅2014年的平均价格Y=3522+385X=3522+385×6=5832（元/m2）。

  • 第9题：

    某类房地产2007—2011年的价格见表2，关于平均增减量法适用条件及其价格趋势值的说法，正确的有（　　）。
    表2　某类房地产2007—2011年的价格（单位：元/m2）

    A．房地产价格的变动过程应是持续上升或持续下降的
    B．各期房地产价格上升或下降的数额应大致相同
    C．2010年的价格趋势值为6900元/m2
    D．2011年的价格趋势值为7283元/m2
    E．2012年的价格趋势值为7634元/m2

    答案：A,B,E
    解析：
    2010年的价格趋势值：d=（6489－5734）÷2=377.5（元/m2），V2010=P0＋d×i=5734＋377.5×3=6866.5（元/m2）；2011年的价格趋势值：d=（6870－5734）÷3=378.67（元/m2），V2011=P0＋d×i=5734＋378.67×4=7248.67（元/m2）；2012年的价格趋势值：d=（7254－5734）÷4=380（元/m2），V2012=P0＋d×i=5734＋380×5=7634（元/m2）。

  • 第10题：

    若动态数列的逐期增长量大体相等，宜拟合（）。

    • A、直线趋势方程
    • B、曲线趋势方程
    • C、指数趋势方程
    • D、二次曲线方程

    正确答案:A

  • 第11题：

    假定被研究现象基本上按不变的发展速度发展，为描述现象变动的趋势，借以进行预测，应拟合的方程是（）。

    • A、直线趋势方程
    • B、曲线趋势方程
    • C、指数趋势方程
    • D、二次曲线方程

    正确答案:C

  • 第12题：

    单选题
    利用直线趋势法对某类商品住宅2005 ~2013年的平均价格进行分析，拟合成一直线趋势方程y= 3522 +385X，其中y为商品住宅价格，X为时间，且Σx=0。经验证该方程拟合度较高，则利用该方程预测该类商品住宅2014年的平均价格为( ) 元/m2。(2014年试题)
    A

    5447

    B

    5832

    C

    6987

    D

    7757


    正确答案： D
    解析：

  • 第13题：

    某类房地产的历史价格变动时高时低，但整体上呈上升趋势，现在要预测该类房地产的未来价格，应选用的预测方法（ ）。

    A．平均发展速度法

    B．平均增减量法

    C．数学曲线拟合法

    D．中位数法


    正确答案：C

  • 第14题：

    用最小平方法拟合出的趋势方程为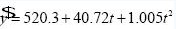：，该方程反映的趋势线是一条( )。

    A．上升直线

    B．下降直线

    C．指数曲线

    D．抛物线


    正确答案：D

  • 第15题：

    需要预测某宗房地产2007年、2008年的价格。通过市场调研，获得该类房地产2002~2006年的价格并计算其逐年上涨额见表2—9。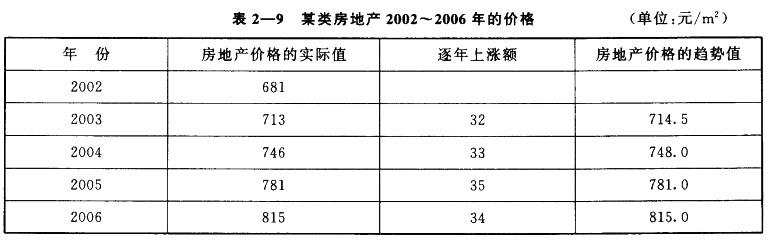

    该类房地产价格逐年上涨额的平均数为（ ）。
    A.32 B.33 C.33.5 D.34


    答案：C
    解析：

  • 第16题：

    利用直线趋势法预测某房地产价格，该城市该类房地产2009年～2019年的价格经过方程拟合得到直线趋势方程Y＝6000＋50X，其中Y为商品住宅价格，X为时间，∑X＝0。经验证，该方程拟合度较高，则利用该方程预测该类商品住宅2020年的平均价格为（ ）元/m2。

    A.6050
    B.6300
    C.6550
    D.6800

    答案：B
    解析：
    本题考查的是数学曲线拟合法。2009年～2019年，过去的数据为11年，为奇数年，所以预测年份2020年的X取6，6000＋50×6＝6300（元/m2）。P385。

  • 第17题：

    利用直线趋势法对某类商品住宅2004～2013年的平均价格进行分析，拟合成一直线趋势方程Y＝3522＋385X，其中Y为商品住宅价格，X为时间，且∑X＝0。经验证该方程拟合度较高，则利用该方程预测该类商品住宅2014年的平均价格为（　）元/m2。

    　　A.5447
    　　B.5832
    　　C.6987
    　　D.7757

    答案：D
    解析：
    本题考查的是数学曲线拟合法。取2008年对应的X＝－1，2009年对应的X＝1，则满足∑X＝0。偶数年，间隔2；奇数年，最中间的数取0，间隔1。



    2014年，X＝11，则Y＝3522＋385×11＝7757（元/m2）。参见教材P385。

  • 第18题：

    某类房地产2006～2010年的价格见下表，根据平均发展速度，预测该类房地产2011年的价格为（　）元/m2。
    　　某类房地产2006～2010年的价格

    A.10300
    B.10400
    C.11165
    D.11265

    答案：C
    解析：
    本题考查的是平均发展速度法的公式。平均发展速度＝=1.24055，2011年的价格＝3800× ＝11165（元/m2）。

  • 第19题：

    关于房地产估价长期趋势运用的说法，正确的有（）。

    A.长期趋势法一般不适用对估价对象当前价格水平的测算或估价
    B.对价格存在明显季节波动的估价对象适宜采用移动平均法消除季节波动影响
    C.数学曲线拟合方程Y=a+ bX的参数a、b通常采用最小二乘法确定
    D.选择具体预测方法的主要依据是估价对象或类似房地产历史价格的变动规律
    E.可以用来比较两类房地产的价格发展潜力

    答案：C,D,E
    解析：
    本题考查的是长期趋势法及其运用。选项B错误，移动平均法是对原有价格按照时间序列进行修匀，即采用逐项递移的方法分别计算一系列移动的时序价格平均数，形成一个新的派生平均价格的时间序列，借以消除价格短期波动的影响，而非季节波动。参见教材P352。

  • 第20题：

    利用直线趋势法对某类商品住宅2010～2019年的平均价格进行分析，拟合成一直线趋势方程Y＝3522＋385X，其中Y为商品住宅价格，X为时间，且∑X＝0。经验证该方程拟合度较高，则利用该方程预测该类商品住宅2020年的平均价格为（ ）元/m2。

    A.5447
    B.5832
    C.6987
    D.7757

    答案：D
    解析：
    本题考查的是长期趋势法中的数学曲线拟合法。取2014年对应的X＝－1，2015年对应的X＝1，则满足∑X＝0。偶数年，间隔2。（若为奇数年数据，最中间的数取0，间隔1）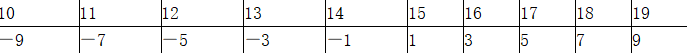

    2020年，X＝11，则Y＝3522＋385×11＝7757。P385。

  • 第21题：

    某类房地产2005~2009年的价格见表1，各年增长量的权重分别为0.1、0.2、0.2、0.5，则利用平均增减量法预测该类房地产2010年的价格为（　　）元/m2。
    表1

    A．8460
    B．8500
    C．8790
    D．8838

    答案：B
    解析：
    由题意，逐年增减量的平均数d=（7130－6810）×0.1+（7460－7130）×0.2+（7810－7460）×0.2+（8150－7810）×0.5=338（元/m2）。则采用逐年上涨额的加权平均数预测该房地产2010年的价格为：V5=P0+d×u=6810+338×5=8500（元/m2）。

  • 第22题：

    某类房地产1994年至1998年的价格分别为910、1190、1490、1810、2110元/m2，按平均增减量趋势法估计，该类房地产于1999年的价格为（）元/m2。

    • A、2390
    • B、2410
    • C、2430
    • D、2450

    正确答案:B

  • 第23题：

    单选题
    某类房地产1994年至1998年的价格分别为910、1190、1490、1810、2110元/m2，按平均增减量趋势法估计，该类房地产于1999年的价格为（）元/m2。
    A

    2390

    B

    2410

    C

    2430

    D

    2450


    正确答案： C
    解析： 暂无解析

相关内容