甲、乙、丙三人将参加某项测试,他们能达标的概率分别是0.8、0.6、0.5,则三人都达标的概率是_________,三人中至少有一人达标的概率是_________。
题目
甲、乙、丙三人将参加某项测试,他们能达标的概率分别是0.8、0.6、0.5,则三人都达标的概率是_________,三人中至少有一人达标的概率是_________。
相似考题
更多“甲、乙、丙三人将参加某项测试,他们能达标的概率分别是0.8、0.6、0.5,则三人都达标的概率是_________,三人中至少有一人达标的概率是_________。”相关问题
-
第1题:
甲、乙两人独立地向同一目标射击,甲、乙两人击中目标的概率分别为0.8,
0.5,两人各射击1次,求至少有1人击中目标的概率.答案:解析:
-
第2题:
若某单位从5位优秀毕业生甲、乙、丙、丁、戊中录用三人,这五人被录用的机会均等,则甲乙中至少一人被录用的概率为: 答案:D解析:
答案:D解析:
-
第3题:
某单位要抽调若干人员下乡扶贫,小王、小李、小张都报了名,但因工作需要,若选小李或小张,就不能选小王。已知三人入选的概率都是0.2,但小李、小张同时入选的概率是0.1,则三人中有人入选的概率是( )《》A.0.3
B.0.4
C.0.5
D.0.6答案:C解析:根据题意“若选小李或小张, 就不能选小王” , 即小李或小张入选时, 小王一定不入选, 小王入选时, 小李和小张都不入选。 “三人中有人入选” 有以下四种情况:
①小李和小张同时入选, 此时小王一定不入选: 概率为 0.1;
②小李入选、 小张不入选, 此时小王一定不入选: 当小李入选时有两类情况: 小李单独入选和小李和小张共同入选,所以小李单独入选的概率为“小李入选的概率小李和小张共同入选的概率”=0.2- 0.1=0.1。.
③小张入选、小李不入选,此时小王一定不入选:当小张入选时有两类情况:小张单独入选和小李和小张共同入选,所以小张单独入选的概率为“小张入选的概率-小李和小张共同入选的概率”=0.2- 0.1=0.1。
④小李与小张都未入选,小王单独入选:概率为0.2。
故“三人中有人入选”的概率是0.1+0.1 +0.1 +0.2=0.5,对应C项。 -
第4题:
甲、乙、丙三位同学参加某单位的招聘面试,面试合格者可正式签约,甲只要面试合格就签约。乙、丙二人约定:只有两人面试都合格才一同签约,否则都不签约。若他们三人面试合格的概率都是 ,且面试是否合格互不影响,则他们三人都没有签约的概率为( )
,且面试是否合格互不影响,则他们三人都没有签约的概率为( )
 答案:B解析:B。概率问题。根据题意,甲没有签约的概率为
答案:B解析:B。概率问题。根据题意,甲没有签约的概率为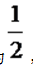 ,乙、丙二人没有签约的概率为
,乙、丙二人没有签约的概率为 ,所以他们三人都没有签约的概率为
,所以他们三人都没有签约的概率为 。B项当选。
。B项当选。
-
第5题:
设甲乙丙三人独立解决某个问题的概率分别为0.45、0.55、0.6,则三人一起解决该问题的概率约为( )。A.0.53
B.0.7
C.0.8
D.0.9答案:D解析:根据题意,三人一起无法解决该问题的概率为(1-0.45) x (1-0.55) x (1-0.6)=0.099。所以,三人一起能解决该问题的概率为1-0.099=0.901。
另一种解题思路是:甲解决了该问题的0.45部分,余下0.55部分没有解决。此时,乙能解决其中的0.55部分,即乙能解决总体的0.55x0.55=0.3025部分。甲乙共解决了45+0.3025=0.7525部分,余下0.2475部分没有解决。丙在其中解决了0.6,即丙解决了总体的0.2475x0.6=0.1485部分。甲乙丙三人共解决了问题0.7525+0.1485=0.901部分。 -
第6题:
“甲、乙、丙三人中至少有一人是本案的知情人。”这个语句所表达的命题,其逻辑常项是()。
正确答案:或者,或者 -
第7题:
已知甲、乙两人击中目标的概率分别为0.7、0.8(两人互不影响),两人均射击一次,则目标被击中的概率为()。
- A、0.8
- B、0.94
- C、0.7
- D、0.72
正确答案:B -
第8题:
某人射击,每次击中目标的概率为0.8。射击3次,至少击中2次的概率约为:()
- A、0.7
- B、0.8
- C、0.5
- D、0.9
正确答案:D -
第9题:
在三次独立重复射击中,若至少有一次击中目标的概率为37/64,则每次射击击中目标的概率为()。
正确答案:1/4 -
第10题:
已知甲、乙两人击中目标的概率分别为0.9、0.8(两人互不影响),两人均射击一次,则两人中只有一人击中目标的概率为()。
- A、0.8
- B、0.18
- C、0.74
- D、0.26
正确答案:D -
第11题:
单选题某人射击,每次击中目标的概率为0.8。射击3次,至少击中2次的概率约为:()A0.7
B0.8
C0.5
D0.9
正确答案: C解析: 暂无解析 -
第12题:
填空题已知甲击中某目标的概率是0.9,乙击中该目标的概率是0.8,现在甲、乙两射手独立地各射击目标一次,则目标仅被甲击中的概率是____,目标仅被乙击中的概率是____,目标不被击中的概率是____.正确答案: 0.18,0.08,0.02解析:
利用独立事件同时发生的概率乘法公式.目标仅被甲击中就是甲击中而乙没击中,其概率为0.9×(1-0.8)=0.18;目标仅被乙击中,则甲没击中,概率为(1-0.9)×0.8=0.08;目标没被击中的概率为(1-0.9)×(1-0.8)=0.02. -
第13题:
设某射手每次射击打中目标的概率为0.5,现在连续射击10次,求击中目标的次数ε的概率分布.又设至少命中3次才可以参加下一步的考核,求此射手不能参加考核的概率.答案:解析:
-
第14题:
甲乙两人各进行射击,甲击中目标的概率是0.3,乙击中目标的概率是0.6,那么两人都击中目标的概率是( )A.0.18
B.0.6
C.0.9
D.1答案:A解析:【考情点拨】本题主要考查的知识点为独立同步试验的概率. 【应试指导】由题意可知本试验属于独立同步试验,应用乘法公式,设甲、乙命中目标的事件分别为A、B,则P(A)=0.3,P(B)=0.6,P(AB)=P(A)·P(B)=0.3×0.6=0.18 -
第15题:
数学运算。通过运算,选择最合适的一项。
甲、乙、丙三位同学参加某单位的招聘面试,面试合格者可正式签约,甲只要面试合格就签约。乙、丙二人约定:只有两人面试都合格才一同签约,否则都不签约。若他们三人面试合格的概率都是 ,且面试是否合格互不影响,则他们三人都没有签约的概率为( )A. B.
B. 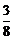 C.
C.  D.
D. 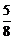 答案:B解析:概率问题。根据题意,甲没有签约的概率为
答案:B解析:概率问题。根据题意,甲没有签约的概率为 ,乙、丙二人没有签约的概率为
,乙、丙二人没有签约的概率为  ,所以他们三人都没有签约的概率为
,所以他们三人都没有签约的概率为 。
。 -
第16题:
设甲乙丙三人独立解决某个问题的概率分别为0.45、0.55、0.6,则三人一起解决该问题的概率约为(53)。A.0.53
B.0.7
C.0.8
D.0.9答案:D解析:根据题意,三人一起无法解决该问题的概率为(1-0.45) x (1-0.55) x (1-0.6)=0.099。所以,三人一起能解决该问题的概率为1-0.099=0.901。
另一种解题思路是:甲解决了该问题的0.45部分,余下0.55部分没有解决。此时,乙能解决其中的0.55部分,即乙能解决总体的0.55x0.55=0.3025部分。甲乙共解决了45+0.3025=0.7525部分,余下0.2475部分没有解决。丙在其中解决了0.6,即丙解决了总体的0.2475x0.6=0.1485部分。甲乙丙三人共解决了问题0.7525+0.1485=0.901部分。 -
第17题:
假设甲、乙、丙三人独立地破译一密码,他们每人译出的概率都是1/4,则密码被译出的概率为()
- A、1/64
- B、1/4
- C、37/64
- D、63/64
正确答案:C -
第18题:
对同一目标进行三次独立射击,第一,二,三次射击的命中概率分别为0.4,0.5,0.7,试求 (1)在这三次射击中,恰好有一次击中目标的概率; (2)至少有一次命中目标的概率。
正确答案: P{三次射击恰击中目标一次}=0.4(1-0.5)(1-0.7)+(1-0.4)0.5(1-0.7)+(1-0.4)(1-0.5)0.7=0.36
P{至少有一次命中}=1-P{未击中一次}=1-(1-0.4)(1-0.5)(1-0.7)=0.91 -
第19题:
甲、乙二人同时在当地开办业务相近的公司,甲失败的概率是0.5,乙失败的概率是0.6,若甲成功的情况下乙能够成功的概率是0.3,则甲或乙至少一人成功的概率是()。
- A、0.6
- B、0.9
- C、0.8
- D、0.75
正确答案:D -
第20题:
甲、乙、丙三人在同一时间内分别破译某个密码,设甲、乙、丙三人能单独译出的概率分别为0.8,0.7和0.6,则密码能被译出的概率为()
正确答案:0.976 -
第21题:
甲、乙两射手各进行一次射击,甲射中目标的概率为0.6,乙射中目标的概率为0.5,则至少有一人射目标的概率是()。
- A、0.30
- B、0.50
- C、0.80
- D、其它
正确答案:C -
第22题:
单选题假设甲、乙、丙三人独立地破译一密码,他们每人译出的概率都是1/4,则密码被译出的概率为()A1/64
B1/4
C37/64
D63/64
正确答案: D解析: 暂无解析 -
第23题:
单选题每次射击时,甲击中目标的概率为0.8,乙击中目标的概率为0.6.甲、乙各自独立地向目标射击一次,则恰有一人击中的概率为( ).A0.44
B0.6
C0.8
D1
正确答案: A解析:
甲、乙各自独立地向目标射击一次,恰有一人击中,即甲击中或者乙击中,则有0.8×0.4+0.2×0.6=0.44.
