(2) 设点P是椭圆C的左准线与 x轴的交点,过点P的直线L与椭圆C相交于M.N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线L的斜率的取值范围。
题目
(2) 设点P是椭圆C的左准线与 x轴的交点,过点P的直线L与椭圆C相交于M.N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线L的斜率的取值范围。
相似考题
更多“(2) 设点P是椭圆C的左准线与 x轴的交点,过点P的直线L与椭圆C相交于M.N两点,当线段MN的中点落在正 ”相关问题
-
第1题:
已知椭圆 和圆
和圆 ,M、N为圆与坐标轴的交点,求证:圆的弦MN是椭圆的切线.答案:解析:
,M、N为圆与坐标轴的交点,求证:圆的弦MN是椭圆的切线.答案:解析:
-
第2题:
椭圆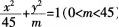 的焦点分别是F1和F2,已知椭圆的离心率
的焦点分别是F1和F2,已知椭圆的离心率
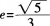 .过中心O
.过中心O
作直线与椭圆交于A,B两点,O为原点,若△ABF2的面积是20。
(1)求m的值;
(2)直线AB的方程。答案:解析:(1)
(2)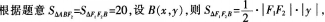
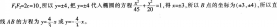
-
第3题:
12、若平面α与β相交于直线l,点P为α与β的公共点,则点P与l的关系是______________
由命题p: ∵m⊥l, ∴m ∥ β或m⊥β或m?β, ∴命题p为假命题; 由命题q得: y=cos(x- π 2 )=cos( π 2 -x)=sinx, ∴y=sinx的图象关于直线x= π 2 对称. ∴命题q为真命题; ∴命题¬q为假命题; 故选B. -
第4题:
已知椭圆C的中心在原点,焦点F1.F2在x轴上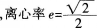 且经过点
且经过点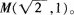
(1)求椭圆C的方程;
(2)如图所示,若直线Z经过椭圆C的右焦点F2且与椭圆C交于A,B两点,使得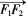
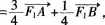 求直线l的方程。
求直线l的方程。 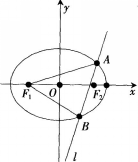 答案:解析:(1)
答案:解析:(1)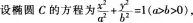

(2)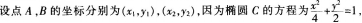
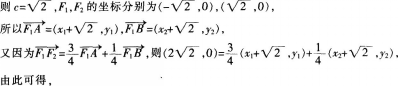

-
第5题:
若平面α与β相交于直线l,点P为α与β的公共点,则点P与l的关系是______________
∵直线l ∥ 平面α,由线面平行的定义知l与α无公共点, 又直线m在平面α内, ∴l ∥ m,或l与m异面, 故选D.
