itgle.com
某防疫站调查甲、乙两小学一年级学生蛔虫感染率均为33％，但甲校抽查250人，乙校抽查150人，两校一年级学生蛔虫感染率95％可信区间为A、甲校较乙校范围大B、乙校较甲校范围大C、甲校较乙校可信度高D、乙校较甲校可信度高E、不具可比性
题目
某防疫站调查甲、乙两小学一年级学生蛔虫感染率均为33％，但甲校抽查250人，乙校抽查150人，两校一年级学生蛔虫感染率95％可信区间为
A、甲校较乙校范围大
B、乙校较甲校范围大
C、甲校较乙校可信度高
D、乙校较甲校可信度高
E、不具可比性
相似考题
更多“某防疫站调查甲、乙两小学一年级学生蛔虫感染率均为33％，但甲校抽查250人，乙校抽查150人，两校一年 ”相关问题
-
第1题：
甲校与乙校学生人数比是4:5，乙校学生人数的3倍等于丙校学生人数的4倍，丙校学生人数的 等于丁校学生人数的 ，又甲校女生占全校学生总数的 ，丁校女生占全校学生总数的 ，且丁校女生比甲校女生多50人，则四校的学生总人数为( )。
A．1920人
B．1865人
C．1725人
D．1640人
正确答案：C
-
第2题：
甲校与乙校学生人数比是4：5，乙校学生人数的3倍等于丙校学生人数的4倍，丙校学生人数的1／5等于丁校学生人数的1／6，又甲校女生占全校学生总数的3／8，丁校女生占全校学生总数的4／9，且丁校女生比甲校女生多50人，则四校的学生总人数为（ ）。
A．1920人
B．1865人
C．1725人
D．1640人
正确答案：C
-
第3题：
甲校学生的英语考试成绩总比乙校学生的英语成绩好，因此，甲校的英语教学方法比乙校的好。
下列选项能加强题干的是：
A甲校英语试题总比乙校的容易
B乙校的英语教师比甲校英语教师工作更勤奋
C乙校选用的英语教材比甲校选用的要难
D甲校学生的英语基础比乙校学生的好答案：B解析：解析:
第一步：找出论点和论据。
英语成绩好推出英语教学方法好。
第二步：逐一分析选项。
A选项，甲校英语试题总比乙校的容易，说明英语成绩好另有它因，削弱了题干；
B选项，乙校的英语教师比甲校英语教师工作更勤奋，还不能得出好成绩，说明教学方法有问题，故加强了题干；
C选项，乙校选用的英语教材比甲校选用的要难，说明英语成绩好另有它因，削弱了题干；
D选项，甲校学生的英语基础比乙校学生的好，说明英语成绩好另有它因，削弱了题干。
故正确答案为B。 -
第4题：
就两校的学生人数看，A、B两校都比C、D两校规模大，要断定E校的学生人数比D校的学生人数多，就需要加上条件（）。A.E校的学生人数比A校多
B.A校的学生人数比B校少
C.E校的学生人数比B校少
D.C校的学生人数比E校少答案：A解析：本题考查的知识点是关系推理中的传递关系推理。传递关系推理的一般形式为：aRb，且bRc，则aRc。所以若要断定E校学生人数比D校的多，就需加上“E校学生人数比A校或B校多”的条件。 -
第5题：
某防疫站调查甲、乙两小学一年级学生蛔虫感染率均为33％，但甲校抽查250人，乙校抽查150人，两校一年级学生蛔虫感染率95％可信区间为A.甲校较乙校范围大
B.乙校较甲校范围大
C.甲校较乙校可信度高
D.乙校较甲校可信度高
E.不具可比性答案：B解析：本资料符合二项分布，总体率的(1－α)置信区间计算公式为（p-Zα/2Sp，p+Zα/2Sp）。p为样本率，Sp为样本率的标准误，两学校的p大小一样，Zα/2大小一样，Sp与p和样本量大小有关系，样本量越大，Sp越小；样本量越小，Sp越大。乙校的调查人数少，所以其Sp比甲校的大，代入公式可知其范围比较大。 -
第6题：
在综合素质考评学期内，甲同学担任学习委员，并兼任了院学生会某部部长；乙同学在隶属校社团联合会的演讲与口才协会担任会长。甲乙两个同学经所在班级和学生会学生干部考核，均考核合格，问甲、乙同学的思想道德素质可以分别加最高多少分（）
- A、甲5分；乙8分
- B、甲8分；乙5分
- C、甲8分；乙8分
- D、甲5分；乙5分
正确答案:D -
第7题：
某校高一的新同学分别乘两辆汽车去市公园游玩。两辆汽车在平直公路上运动，甲车内一同学看见乙车没有运动，而乙车内一同学看见路旁的树木向西移动。如果以地面为参考系，那么，上述观察说明（）
- A、甲车不动，乙车向东运动
- B、乙车不动，甲车向东运动
- C、甲车向西运动，乙车向东运动
- D、甲、乙两车以相同的速度都向东运动
正确答案:D -
第8题：
甲和乙约定，若甲的儿子考上大学，甲则把其子使用的一辆汽车卖给乙，并约定汽车应在甲的儿子入校后3个月内交付。后来甲的儿子如愿考上大学，而甲未履行合同义务，则甲乙两人合同的诉讼时效期间应自（）时起算。
- A、甲的儿子入校
- B、甲的儿子考上大学
- C、甲的儿子入校满3个月
- D、双方达成协议时
正确答案:C -
第9题：
问答题某校在讨论出国进修人选时，有两种不同意见。（1）如果甲去，那么乙不去。（2）甲和乙都去。当问王校长的意见时，王说：“这两种意见都不对，我主张乙去，甲不去。”请问，王校长的意见是否违反逻辑基本规律的要求？为什么？正确答案： “如果甲去，那么乙不去”等值于“甲不去，或者乙不去”，它与“甲和乙都去”具有矛盾关系。王校长同时否定这两种具有矛盾关系的意见，违反排中律。解析： 暂无解析 -
第10题：
单选题从甲乙两所重点学校中各抽取一个班进行数学统考，对平均数做卡方检验，结果保留零假设Ho，说明两所学校的成绩：（）A有本质差异
B无本质差异
C甲校成绩优于乙校
D乙校成绩优于甲校
正确答案： C解析： 暂无解析 -
第11题：
单选题检查甲校12岁男生300人，有龋人数为140人，检查乙校同年龄男生500人，有龋人数为150人，想要比较两校学生龋病情况，应采用下列哪项统计指标？（ ）A标准差
B构成比
C平均数
D百分率
E标准误
正确答案： E解析：
平均数是反映一组性质相同的观察值的平均水平或集中趋势的统计指标。标准差是用来说明一组观察值之间的变异程度。标准误是用来表示抽样误差的大小。百分率是用来说明某种现象发生的频率或强度，常用来表示人群中疾病状况的高低。构成比是用来说明某事物内部名构成部分所占的比重。 -
第12题：
单选题某卫生防疫站调查甲、乙两学校二年级学生蛔虫感染率均为33%，但甲校调查300人，乙校调查135人，两校蛔虫感染率95%置信区间（）A甲校比乙校范围大
B乙校比甲校范围大
C甲校比乙校可信程度高
D乙校比甲校可信程度高
E以上都不正确
正确答案： D解析： 暂无解析 -
第13题：
甲、乙两校共有毕业生180人，两校各买了一批纪念册，给本校毕业生每人一本后，甲校余116本，乙校余114本。经研究两校各向彼校毕业生每人送一本纪念册，送后甲校还比乙校多剩10本。问甲校的毕业生人数比乙校的毕业生人数多多少人？()
A.20人
B．16人
C．10人
D．8人
正确答案：D
由题意知，两校各给本校毕业生每人一本后共余下116 +114 - 230（本）。两校再各向彼校毕业生每人送一本后共余下230-180- 50（本）．而这时甲校比乙校多余下10本，故知此时甲校还余下(50+10)÷2-30（本）．乙校还余下(50 -10)÷2-20（本）。而两校各给对方每个毕业生送了一本后，相当于两校买的纪念册各发了180本，所以甲校买了30+180 - 210（本）．乙校买了20+180=200（本）．甲、乙两校的毕业生人数分别是210 -116 - 94（人），200-114= 86（人）。二者相差94-86-8（人）。故选D。[解二]第一次分发毕业纪念册后，甲校余下的比乙校多116 -114 -2（本）．给彼校分发完毕后，甲校比乙校剩余的多10本，由此可推断甲校学生比乙校多10 - 2-8（人），故选D。
-
第14题：
某旅行杜拟在暑假期间面向学生推出“林州红旗渠一日游”活动，收费标准如下：
人数m
0＜m≤100
100＜m≤200
m＞200
收费标准（元/人）
90
85
75
甲、乙两所学校计划组织本校学生自愿参加此项活动．已知甲校报名参加的学生人数多于100人，乙校报名参加的学生人数少于100人．经核算，若两校分别组团共需花费20800元，若两校联合组团只需花赞18000元．
（1）两所学校报名参加旅游的学生人数之和超过200人吗？为什么？
（2）两所学校报名参加旅游的学生各有多少人？
正确答案：考点：二元一次方程组的应用。
专题：方程思想。
分析：（1）由已知分两种情况讨论，即a＞200和100a≤200，得出结论；
（2）根据两种情况的费用，即a＞200和100a≤200分别设未知数列方程组求解，讨论得出答案．
解答：解：（1）设两校人数之和为a．
若a＞200，则a=18000÷75=240．
若100a≤200，则
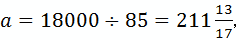，不合题意．所以这两所学校报名参加旅游的学生人数之和等于240人，超过200人．
（2）设甲学校报名参加旅游的学生有x人，乙学校报名参加旅游的学生有y人，则
①当100x≤200时，得
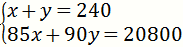
解得
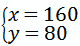（6分）②当x＞200时，得
解得
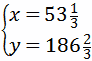
此解不合题意，舍去．
∴甲学校报名参加旅游的学生有160人，乙学校报名参加旅游的学生有80人．
点评：此题考查的是二元一次方程组的应用，关键是把不符合题意的结论舍去．
-
第15题：
已知甲校学生人数是乙校学生人数的40%，甲校女生人数是甲校学生人数的30%,乙校 男生人数是乙校学生人数的42%，那么，两校女生总数占两校学生总数的（ ）。
A. 30%
B. 50%
C. 40%
D. 60%答案：B解析：设甲校有200人，则乙校有200 ÷ 40% = 500 (人），甲校女生有 200×30% = 60(人），乙校有女生500×(1 —42%) = 290(人），两校女生共350人，两校学生共 700人，所以女生总数占50%。 -
第16题：
现有甲、乙两所学校，根据上年度的经费实际投入统计，若仅仅比较在校本科生的学生人均投入经费，甲校高于乙校的86%；但若比较所有学生（本科生加上研究生）的人均经费投入，甲校是乙校的118%。各校研究生的人均经费投入均高于本科生。根据以上信息，最可能得出以下哪项？A.上年度，甲校学生总数多于乙校。
B.上年度，甲校研究生人数少于乙校。
C.上年度，甲校研究生占该校学生的比例高于乙校。
D.上年度，甲校研究生人均经费投入高于乙校。
E.上年度，甲校研究生占该校学生的比例高于乙校，或者甲校研究生人均经费投入高于乙校答案：E解析：根据题干条件，甲乙两所院校仅比较本科生人均经费和比较所有学生人均经费的结果有较大差异，说明导致差异的原因是研究生学生在所有学生所占的比例或研究生的投入经费是不同的。如果研究生所占比例低，则所有学生的人均经费比单独计算本科生高；如果研究生投入人均经费高，也会使所有学生的人均经费比单独计算本科生高些。所以E项最可能推出。C和D不能选，根据p真推出p或q真，可知C真和D真逗可推出E真，这样就多个选项为真。 -
第17题：
甲校学生的数学考试成绩比乙校学生的数学考试成绩好，因此，甲校的数学教学方法比乙校好。除以下哪项而外，其余各项若真者会削弱上述结论？A.甲校的数学考试题总比乙校学生好
B.甲校学生的数学基础比乙校学生好
C.乙校选用的数学教材比甲校难
D.乙校的数学老师比甲校的工作更勤奋
E.乙校学生数学课的课时比甲校少答案：D解析： -
第18题：
某校在讨论出国进修人选时，有两种不同意见。（1）如果甲去，那么乙不去。（2）甲和乙都去。当问王校长的意见时，王说：“这两种意见都不对，我主张乙去，甲不去。”请问，王校长的意见是否违反逻辑基本规律的要求？为什么？
正确答案: “如果甲去，那么乙不去”等值于“甲不去，或者乙不去”，它与“甲和乙都去”具有矛盾关系。王校长同时否定这两种具有矛盾关系的意见，违反排中律。 -
第19题：
从甲乙两所重点学校中各抽取一个班进行数学统考，对平均数做卡方检验，结果保留零假设Ho，说明两所学校的成绩：（）
- A、有本质差异
- B、无本质差异
- C、甲校成绩优于乙校
- D、乙校成绩优于甲校
正确答案:B -
第20题：
单选题“甲公司欲赠乙校一批电脑，于是委托公民丙以甲公司的名义与丁企业签订了这份电脑买卖合同。在此活动中买卖行为的代理人是（）。A甲公司
B乙校
C公民丙
D丁企业
正确答案： C解析： 暂无解析 -
第21题：
单选题某疾控中心调查甲、乙两学校二年级学生蛔虫感染率均为33%，但甲校调查300人，乙校调查135人，两校蛔虫感染率95%置信区间（）。A甲校比乙校范围大
B乙校比甲校范围大
C甲校比乙校可信程度高
D乙校比甲校可信程度高
E以上都不正确
正确答案： A解析： 暂无解析 -
第22题：
问答题一项调查反映出的学校组织形式的变化 在调查中发现，新课程实施的学校组织结构产生的变化，从不同学校的对比中会发现一些有意义的变化。 1.教研组和备课组：甲、乙校之同甲、乙两校中，按学科划分组，每组有一名老教师，其余为年轻教师。这种组织给教师提供了许多合作交流的机会。通过这种合作，教师们解决了许多新课程实施中遇到的问题。教研组、备课组内教师年龄、资历的合理搭配也使这种组织更加有效。两校的老师反响普遍较好。 2.教科处：甲、乙校之异这是乙校为实施新课程专门设立的机构，其主要职责是处理与新课程有关的教师培训、课程设置、人员调配以及学校之间的评课、参观等交流工作。除教科处主任外，一位副校长也主管新课程改革的有关事宜。对此，年轻老师和年纪大的教师比较支持，年龄处于中间的教师接受程度较差。 与之相比，甲校并没有因为新课程改革而另外设置机构。甲校由于人员、编制等问题无法额外安排专门人员负责新课程改革。甲校校长认为教师对新课程改革有问题时可以向教导处咨询，如果是学科内部问题可以向同事、校长咨询。而甲校教师却认为教导处、校长这些只是行政机构，绝大多数问题都是教师内部解决。结合上述案例，对比甲乙两校的做法谈谈案例给你的启示。正确答案： 1.教研组的负面效应。同学科之间合作大于不同学科。学校应该打破学科限制。
2.教科处的实质作用，促进了乙校新课程实施。
3.课程改革的实施需要经过不同层次，经历不同程度的深化。尽管需要较长时间，但一旦成功，其影响是巨大的。
4.教材、资源的改革是最容易实施的。
5.要建立新的组织方式、教学活动方式、理解掌握相关的知识与方法，形成价值观。解析： 暂无解析 -
第23题：
单选题某卫生防疫站调查甲、乙两学校二年级学生蛔虫感染率均为33%，但甲校调查300人。乙校调查135人，两校蛔虫感染率95%可信区间（ ）。A甲校比乙校范围大
B甲校比乙校可信程度高
C乙校比甲校范围大
D乙校比甲校可信程度高
E以上都不正确
正确答案： C解析： 暂无解析