itgle.com

盒中有4个白球6个红球，无放回地每次抽取1个，则第二次取到白球的概率是 A. 2/15 B. 4/15 C. 2/5 D. 3/5

题目
盒中有4个白球6个红球，无放回地每次抽取1个，则第二次取到白球的概率是


A. 2/15
B. 4/15
C. 2/5
D. 3/5
相似考题

1.袋中有5个球,3个新2个旧,每次取一个,无放回地取两次,则第二次取到新球的概率是()A、3/5B、3/4C、1/2D、3/10

2.一个袋内装有10个球，其中有3个白球，5个红球，2个黑球采取不放回抽样，每次取1件，则第二次取到的是白球的概率是()A、0.6B、0.5C、0.4D、0.3

3.一个袋子里有10个小球，其中4个白球，6个黑球，无放回地每次抽取1个，则第二次取到白球的概率是多少？（ ）

4.一口袋装有6只球，其中4只白球、2只红球。从袋中取球两次，每次随机地取一只。采用不放回抽样的方式，取到的两只球中至少有一只是白球的概率()A、4/9B、1/15C、14/15D、5/9

参考答案和解析
答案：C
解析：
解题指导： 初步学习过概率的考生可能选择用条件概率去做。方法如下：第一次取到白球，第二次取到白球；（4/10）×3/9=12/90。第一次取到黑球，第二次取到白球。（6/10）×4/9=24/90。12/90+24/90=36/90=2/5。故答案为C。
更多“盒中有4个白球6个红球，无放回地每次抽取1个，则第二次取到白球的概率是 ”相关问题

  • 第1题：

    盒内装有10个白球，2个红球，每次取1个球，取后不放回。任取两次，则第二次取得红球的概率是：

    A. 1/7
    B.1/6
    C.1/5
    D. 1/3

    答案：B
    解析：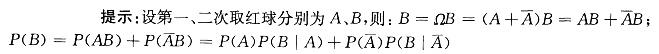

    或“试验分两步，求第二步结果的概率”用全概率公式。

  • 第2题：

    一个盒子中5个红球,5个白球,现按照如下方式,求取到2个红球和2个白球的概率.
    　　(1)一次性抽取4个球；(2)逐个抽取,取后无放回；(3)逐个抽取,取后放回.


    答案：
    解析：
    【解】(1)设A1={一次性抽取4个球，其中2个红球2个白球），则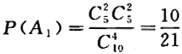
    (2)设A2={逐个抽取4个球，取后不放回，其中2个红球2个白球}，则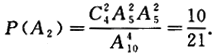

    (3)设A3={逐个抽取4个球，取后放回，其中2个红球2个白球}，则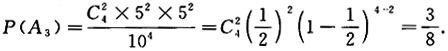

  • 第3题：

    设口袋中有10只红球和15只白球,每次取一个球,取后不放回,则第二次取得红球的概率为_______.


    答案：
    解析：
    设A1={第一次取红球)，A2={第一次取白球），B={第二次取红球），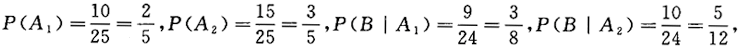　　

    则
    　　

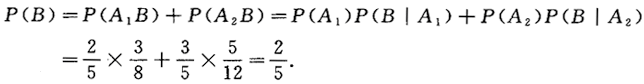
  • 第4题：

    袋中有50个球，其中20个新球，30个旧球，现每次取1球，无放回地取2次，则第2次取得旧球的概率是()。



    答案：A
    解析：

  • 第5题：

    一个袋子里有8个黑球，8个白球，随机不放回连续取球5次，每次取出1个球，求最多取到3个白球的概率. .?


    答案：
    解析：

  • 第6题：

    一个口袋中有7个红球3个白球,从袋中任取一球,看过颜色后是白球则放回袋中，直至取到红球,然后再取一球，假设每次取球时各个球被取到的可能性相同，求第一、第二次都取到红球的概率（ ）。

    A.7/10
    B.7/15
    C.7/20
    D.7/30

    答案：B
    解析：
    设AB分别表演一、二次取红球，则有P（AB）=P（A）P（B|A）=7/106/9=7/15。

  • 第7题：

    一袋中有2个黑球和若干个白球，现有放回地摸球4次，若至少摸到一个白球的概率是80/81，则袋中白球的个数是（）。


    正确答案:4

  • 第8题：

    设袋中有2个黑球、3个白球，有放回地连续取2次球，每次取一个，则至少取到一个黑球的概率是（）


    正确答案:16/25

  • 第9题：

    单选题
    一个袋子里有10个小球，其中4个白球，6个黑球，无放回地每次抽取1个，则第二次取到白球的概率是多少？（　　）
    A

    2/15

    B

    4/15

    C

    1/5

    D

    2/5


    正确答案： D
    解析：
    可分成两种情况：①第一次取到白球，第二次也取到白球的概率是：4/10×3/9＝12/90；②第一次取到黑球，第二次取到白球的概率是：6/10×4/9＝24/90，即第二次取到白球的概率为24/90＋12/90＝2/5。

  • 第10题：

    问答题
    38.当袋中有2个白球3个红球．现从袋中随机地抽取2个球，以X表示取到的红球个数。求X的分布律．

    正确答案：
    解析：

  • 第11题：

    单选题
    袋中共有5个球，其中3个新球，2个旧球，每次取1个，无放回地取2次，则第二次取到新球的概率是（）．
    A

    3/5

    B

    3/4

    C

    1/2

    D

    3/10


    正确答案： D
    解析： 根据古典概率的定义可以得知

  • 第12题：

    一个袋子里放有10个小球(其中4个白球，6个黑球)，无放回地每次抽取1个，则第二次取到白球的概率是（ ）

    A. 2/15
    B. 4/15
    C. 1/5
    D. 2/5

    答案：D
    解析：
    解题指导： 第一次取到白球，第二次取到白球的机率为4/10*3/9=2/15 ；第一次取到黑球，第二次取到白球的机率为6/10*4/9=4/15 。可知，第二次取到白球的机率为4/15+2/15=2/5,故答案为D。

  • 第13题：

    现有三个箱子,第一个箱子有4个红球,3个白球；第二个箱子有3个红球,3个白球；第三个箱子有3个红球,5个白球；先取一只箱子,再从中取一只球,(1)求取到白球的概率；(2)若取到红球,求红球是从第二个箱子中取出的概率.


    答案：
    解析：

  • 第14题：

    袋中有1个红球、2个黑球与3个白球，现有放回地从袋中取两次，每次取一个球.以X，Y，Z分别表示两次取球所取得的红球、黑球与白球的个数.
    (Ⅰ)求P{X=1｜Z=0}；
    (Ⅱ)求二维随机变量(X，Y)的概率分布.


    答案：
    解析：

  • 第15题：

    袋中有l个红球、2个黑球与3个白球，现有放回地从袋中取两次，每次取一个球，以X，y，Z分别表示两次取球所取得的红球、黑球与白球的个数。
    (1)求
    (2)求二维随机变量(X，Y)的概率分布。


    答案：
    解析：

  • 第16题：

    一个袋子里有8个黑球，8个白球，随机不放回地连续取球五次。每次取出1个球，求最多取到3个白球的概率。


    答案：
    解析：

  • 第17题：

    袋中共有5个球，其中3个新球，2个旧球，每次取1个，无放回地取2次，则第二次取到新球的概率是（）．

    • A、3/5
    • B、3/4
    • C、1/2
    • D、3/10

    正确答案:A

  • 第18题：

    一口袋有6个白球，4个红球，“无放回”地从袋中取出3个球，则事件“恰有两个红球”的概率为（）


    正确答案:3/10

  • 第19题：

    袋中有大小相同的黑球7只，白球3只，每次从中任取一只，有放回抽取，记首次抽到黑球时抽取的次数为X，则P{X＝10}＝（）。


    正确答案:0.39*0.7

  • 第20题：

    填空题
    一袋中有50个乒乓球，其中20个红球，30个白球，今两人从袋中各取一球，取后不放回，则第二个人取到红球的概率为____。

    正确答案： 2/5
    解析：
    设A：“第一个人取红球”，B：“第二个人取红球”，则
    P（B）＝P[B（A∪A(＿)）]＝P（AB）＋P（A(＿)B）＝P（B|A）P（A）＋P（B|A(＿)）P（A(＿)）＝（19/49）×（20/50）＋（20/49）×（30/50）＝2/5

  • 第21题：

    问答题
    8.袋中有7个球，其中红球5个白球2个，从袋中取球两次，每次随机地取一个球，取后不放回，求：    (1)第一次取到白球、第二次取到红球的概率；    (2)两次取得一红球一白球的概率．

    正确答案：
    解析： 暂无解析

相关内容