有甲乙两个工程队负责某小区主干道维修及墙面粉刷。主干道维修,如果两个工程队合作,30天完成,若乙工程队单独进行,105天完成;粉刷墙面,若两个工程队合作,28 天完成,若甲工程队单独做,140 天完成。如果两项工作两个工程队共同分工合作,最少需要多少天?A.34 B.35 C.40 D.41
题目
有甲乙两个工程队负责某小区主干道维修及墙面粉刷。主干道维修,如果两个工程队合作,30天完成,若乙工程队单独进行,105天完成;粉刷墙面,若两个工程队合作,28 天完成,若甲工程队单独做,140 天完成。如果两项工作两个工程队共同分工合作,最少需要多少天?
A.34
B.35
C.40
D.41
B.35
C.40
D.41
相似考题
参考答案和解析
答案:C
解析:

更多“ 有甲乙两个工程队负责某小区主干道维修及墙面粉刷。主干道维修,如果两个工程队合作,30天完成,若乙工程队单独进行,105天完成;粉刷墙面,若两个工程队合作,28 天完成,若甲工程队单独做,140 天完成。如果两项工作两个工程队共同分工合作,最少需要多少天?”相关问题
-
第1题:
两个工程队修一公路,甲工程队10天修了45公里,乙工程队以比甲工程队快两倍的速度修了15天,问乙工程队修了多少公里?( )
A.102.5公里
B.202.5公里
C.135公里
D.235公里
正确答案:C
甲工程队每天修45÷10=45公里,则乙工程队每天修4.5×2=9公里,乙工程15天修15×9=135公里。正确答案为C。 -
第2题:
甲乙两个工程队承担了精准扶贫村公路的修筑任务,先是甲工程队单独修了10天,完成了总工程的四分之一,接着乙工程队加入合作,完成剩余工程。在第14天完成到总工程的一半,则按照这种进度完成全部工程所用的天数比由甲单独完成这项工程少用的天数是A.12天
B.20天
C.18天
D.16天答案:C解析:第一步,本题考查工程问题,要熟悉工程量、工作时间和工作效率三者之间的比例关系。第二步,甲完成四分之一需要10天,则完成全部工程需要40天;甲乙合作后在第14天完成一半,即甲和乙合作4天完成四分之一,剩下的一半甲和乙合作需要8天,即一共需要14+8=22天完成,则比甲单独完成这项工程少用的天数为18天。因此,选择C选项。 -
第3题:
数学运算。通过运算,选择最合适的一项。
甲、乙两个工程队需要在规定的工期内完成某项工程。若甲、乙两队合作,则恰好能按期完成;若甲的效率提高{图} ,乙的效率提高 {图1},则用原定工期的{图2} 即可完成;若乙的效率降低{图3} ,则需要推迟2天才能完成。那么,该工程原定的工期为( )A.10天 B.12天 C.16天 D.18天答案:D解析:假设甲、乙原来的效率分别为a和b;提速前后时间比为7︰5、效率比为5︰7,则有a+b=5、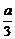 +
+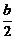 =7-5,可得a=3,b=2。减速前后效率之比为5︰[3+2×(1-
=7-5,可得a=3,b=2。减速前后效率之比为5︰[3+2×(1-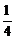 )]=5︰4.5=10︰9,时间比为9︰10,差1份对应2天,则原来的时间9份对应18天。
)]=5︰4.5=10︰9,时间比为9︰10,差1份对应2天,则原来的时间9份对应18天。 -
第4题:
有甲乙两个工程队负责某小区主干道维修及墙面粉刷。主干道维修,如果两个工程队合作,30天完成,若乙工程队单独进行,105天完成;粉刷墙面,若两个工程队合作,28天完成,若甲工程队单独做,140天完成。如果两项工作两个工程队共同分工合作,最少需要多少天?A.34
B.35
C.40
D.41答案:C解析:第一步,本题考查工程问题,属于时间类,用赋值法解题。
第二步,赋值维修主干道的总量为1050(30和105的公倍数),则甲乙合作的效率为1050÷30=35,乙的效率为1050÷105=10,则甲的效率为35-10=25;赋值墙面粉刷的总量为140(28和140的公倍数),则甲乙合作的效率为140÷28=5,甲的效率为140÷140=1,则乙的效率为5-1=4。可知,甲维修主干道的效率比乙高,乙粉刷墙面的效率比甲高。
第三步,问项目最少需要多少天,则甲和乙做自己效率更高的项目。所以由甲维修主干道,乙负责墙面粉刷。乙粉刷墙面需要140÷4=35(天),而甲35天可以维修道路的工作量为35×25=875。
第四步,维修道路剩余工作量为1050-875=175,剩余工作量由甲乙合作完成,还需要175÷35=5(天)。故一共需要35+5=40(天)。 -
第5题:
甲、乙两个工程队修公路,甲工程队修500米后由乙工程队来修,由以往资料显示乙工程队的效率是甲工程队的两倍,乙工程队修600米的时间比甲工程队修500米的时间少20天,甲工程队的工作效率为( )米/天。A.20
B.15
C.10
D.25答案:C解析:根据甲、乙效率比可知,相同时间,乙修600米,甲修300米。即甲修300米所用时间比其修500米所用时间少20天,故甲修200米用20天,每天修200÷20=10(米)。 -
第6题:
甲工程队与乙工程队的效率之比为4:5,一项工程由甲工程队单独做6天,再由乙工程队单独做8天,最后由甲、乙两个工程队合作4天刚好完成,如果这项工程由甲工程队或乙工程队单独完成,则甲工程队所需天数比乙工程队所需天数多多少天?A.3
B.4
C.5
D.6答案:C解析: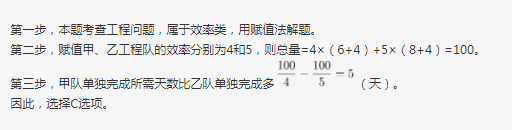
-
第7题:
甲、乙两个工程队合作完成某工程需36天,若甲工程队先做10天,剩下的工程再由两队合作30天完成。问乙工程队的工作效率是甲工程队的: 答案:A解析:第一步,本题考查工程问题,属于时间类。
答案:A解析:第一步,本题考查工程问题,属于时间类。
第二步,设甲、乙工程队的工作效率分别为x、y,根据题意可列出等式:36(x+y)=10x+30(x+y),化简得y∶x=2∶3。
因此,选择A选项。 -
第8题:
一项工程,如果甲工程队先做8天,那么乙工程队需要再做16天就可以完成;如果乙工程队先做8天,那么甲工程队再做10天就可以完成;如果甲工程队先做5天,再由两个工程队合作完成,则一共需要( )天完成。
A. 3.2
B. 5.3
C. 10.6
D. 12.8答案:C解析:本题考查工程问题。设甲的效率为x,乙的效率为y,则有8x+16y=8y+10x,解得x=4y。赋值x=4,y=1,则总量为48。甲5天完成20,剩余28由甲乙完成,需要28÷5=5.6天,共10.6天。因此,本题答案为C选项。 -
第9题:
甲、乙两个工程队合作完成某工程需36天,若甲工程队先做10天,剩下的工程再由两队合作30天完成。问乙工程队的工作效率是甲工程队的:A.2/3
B.4/5
C.3/4
D.1/2答案:A解析:本题属于工程问题。
设甲工程队的效率为x,乙工程队的效率为y。根据工程总量不变可列式:36×(x+y)=10x+30×(x+y),化简得2x=3y,即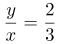 },即乙工程队的工作效率是甲工程队的{图1。
},即乙工程队的工作效率是甲工程队的{图1。
因此,选择A选项。 -
第10题:
一项小工程由甲乙两个工程队合作需要12小时,由乙丙两个工程队合作需要15小时,由甲丙两个工程队合作需要18小时,那么这项工程由甲乙丙三个工程队合作大约需要多少小时完成?()
- A、9.7
- B、8.7
- C、10.2
- D、11.3
正确答案:A -
第11题:
单选题工程队接到一项工程,投入80台挖掘机。如连续施工30天,每天工作10小时,正好按期完成。但施工过程中遭遇大暴雨,有10天时间无法施工。工期还剩8天时,工程队增派70台挖掘机并加班施工。若工程队想按期完成,则平均每天需多工作多少个小时( )A1.5
B2
C2.5
D3
正确答案: A解析: -
第12题:
单选题甲乙两个工程队承担了精准扶贫村公路的修筑任务,先是甲工程队单独修了 10 天,完成了总工程的四分之一,接着乙工程队加入合作,完成剩余工程。在第 14 天完成到总工程的一半,则按照这种进度完成全部工程所用的天数比由甲单独完成这项工程少用的天数是A18 天
B16 天
C12 天
D20 天
正确答案: A解析: 暂无解析 -
第13题:
甲、乙两个工程队共同完成A和B两个项目。已知甲队单独完成A项目需13天,单独完成B项目需7天;乙队单独完成A项目需11天,单独完成B项目需9天。如果两队合作用最短的时间完成两个项目,则最后一天两队需要共同工作多长时间就可以完成任务?( ) 答案:D解析:分析题干得知,甲完成B项目,乙完成A项目,然后甲乙共同完成剩余的A项目,这样的时间最短。即B项目完工时,乙做A项目已7天。令A工程总量为11X13 = 143,则甲效率为11,乙效率为13,B项目完工时,A项目剩余143-13X7 = 52,所以完成A项目还需52/(11+13)=13/6天,最后一天需要共同工作1/6天。答案选择D。
答案:D解析:分析题干得知,甲完成B项目,乙完成A项目,然后甲乙共同完成剩余的A项目,这样的时间最短。即B项目完工时,乙做A项目已7天。令A工程总量为11X13 = 143,则甲效率为11,乙效率为13,B项目完工时,A项目剩余143-13X7 = 52,所以完成A项目还需52/(11+13)=13/6天,最后一天需要共同工作1/6天。答案选择D。 -
第14题:
某工程50人进行施工。如果连续施工20天,每天工作10小时,正好按期完成。但施工过程中遭遇原料短缺,有5天时间无法施工,工期还剩8天时,工程队增派15人并加班施工。若工程队想按期完成,则平均每天需工作( )小时。A.12.5
B.11
C.13.5
D.11.5答案:A解析:第一步,本题考查工程问题,属于条件类,用方程法解题。
第二步,赋值每人每小时的工作效率为1,由题意得工程总量为50×20×10=10000。有5天时间无法施工,且剩8天时又增派15人加班施工,那么后8天有65人施工,前20-8-5=7(天)有50人施工。
第三步,设平均每天工作t小时,由总量不变可列方程:7×50×10+8×65×t=10000,解得t=12.5。 -
第15题:
由于汛期暴雨某路段发生塌陷,要进行抢修,需在规定日期内完成,如果由甲工程队修,恰好按期完成;如果由乙工程队修,则要超过规定日期3天。如果两个工程队合作了2天,余下的部分由乙工程队单独做,正好在规定日期内完成。则规定日期的天数是:A. 4
B. 5
C. 6
D. 7答案:C解析:
-
第16题:
有甲乙丙三个工程队参加清理一条河道的任务,已知他们单独完成清理任务的工作时间之比为4:5:8,若甲乙两个工程队先合作工作4天,剩下的工程量是总量的十分之一,剩下部分由丙队单独完成,则丙需要再做( ) 天才能完成。(注:结果若有小数,请四舍五入,保留整数位。)A.2
B.3
C.1
D.4答案:A解析:根据*他们单独完成清理任务的工作时间之比为4:5:8”赋甲乙丙工作效率分别为10、8、5, 甲乙先合作4天共完成4X (10+8) -72,由题意可知这完成的是总最的十分之九,则总量为80,剩余的工作量为8,则剩余的丙需要8+ 5=1.6≈2天才能完成,A选项正确,B、C. D选项错误。故本题应选A。 -
第17题:
甲、乙工程队需要在规定的工期内完成某项工程。若甲队单独做,则要超工期9天完成;若乙队单独做,则要超工期16天才能完成;若两队合做,则恰好按期完成。那么,该项工程规定的工期是( )A.8天 B.6天 C.12天 D.5天答案:C解析:解法一:假设规定的工期为x天,对比“若甲队单独做,则要超工期9天完成”和“若两队合做,则恰好按期完成”可知,甲队(超工期)9天完成的工程量恰好就是乙队在规定工期x天内完成的工程量。又由题意可得甲队工作效率大于乙队,则x>9,观察选项发现C项符合。
解法二:假设规定的工期为x天,对比“若甲队单独做,则要超工期9天完成”和“若两队合做,则恰好按期完成”可知,甲队(超工期)9天完成的工程量恰好就是乙队在规定工期x天内完成的工程量,即9×甲队工作效率=x×乙队工作效率。同理可得,乙队(超工期)16天完成的工程量恰好就是甲队在规定工期x天完成的工程量,即16×乙队工作效率=x×甲队工作效率。上述两等式左右两边分别相乘,然后化简得x=12。C项正确。 -
第18题:
一项工程由甲、乙工程队单独完成,分别需50天和80天。若甲、乙工程队合作20天后,剩余工程量由乙、丙工程队合作需12天完成,则丙工程队单独完成此项工程所需的时间是A.40天
B.45天
C.50天
D.60天答案:D解析:
-
第19题:
甲、乙两个工程队共同完成A和B两个项目。巳知甲队单独完成A项目需13天,单独完成B项目需7天;乙队单独完成A项目需11天,单独完成B项目需9天。如果两队合作用最短的时间完成两个项目,则最后一天两队需要共同工作多长时间就可以完成任务?( )
A.1/12天 B.1/9天 C.1/7天 D. 1/6天答案:D解析:分析题干得知,甲完成B项目,乙完成A项目,然后甲乙共同完成剩余的A项目,这样的时间最短。即B项目完工时,乙做A项目已7天。令A工程总量为11X13 = 143,则甲效率= 11,乙效率=13,B项目完工时,A项目剩余143-13 X 7 = 52,所以完成A项目还需52 / (11 + 13) = 13/6天,最后一天需要共同工作1/6天。答案选择D。 -
第20题:
某工程由甲、乙两工程队合作需要10天完成,乙、丙两个工程队合作需要7天完成,甲、乙、丙三个工程队合作需要5天完成。现甲、乙、丙三个工程队同时工作,2天后,乙工程队因有其他任务撤离该工程,问甲、丙两个工程队还需多少天能完成该工程?( )A.3
B.4
C.5
D.6答案:B解析:设工程总量为70,则甲的效率+乙的效率=70÷10=7,乙的效率+丙的效率=70÷7=10,甲的效率+乙的效率+丙的效率=70÷5=14,则甲的效率=14-10=4,丙的效率=14-7=7。甲、乙、丙前两天共同完成的工作量=14×2=28,剩余工作量=70-28=42。甲、丙同时完成剩余工作量需要天数=42÷(4+7)≈3.8(天),故答案为B。 -
第21题:
某市有甲、乙、丙三个工程队,有一个工程需要三个工程队合作完成,已知甲队单独完成这项工程需要10天,乙队单独完成这项工程需要8天,丙队单独完成这项工程需要15天。现三队合作,但甲队因故只参加了3天,丙队也休息了若干天,最后该工程用了4天完成,则丙队休息的天数是()
- A、1
- B、2
- C、3
- D、4
正确答案:A -
第22题:
单选题现有一项工程需要甲、乙、丙三个工程队去完成,已知甲、乙两队合作需要10天,甲、丙两队合作需要12天,乙、丙两队合作需要15天,则三队共同合作完成需要多少天?A5
B6
C7
D8
正确答案: B解析: -
第23题:
单选题甲、乙两个工程队共同完成A.和B.两个项目,已知甲队单独完成A.项目需13 天,单独完成B.项目需7 天;乙队单独完成A.项目需11 天,单独完成B.项目需9 天。如果两队合作用最短的时间完成两个项目,则最后一天两队需要共同工作多少时间就可以完成任务:A1/12天
B1/9天
C1/7天
D1/6天
正确答案: D解析:
