树的带权路径长度为树中所有叶子结点的()。
题目
相似考题
参考答案和解析
略
更多“树的带权路径长度为树中所有叶子结点的()。”相关问题
-
第1题:
利用3、 6、8、12这四个值作为叶子结点的权,生成一棵哈夫曼树,该树中所有叶子结点中的最长带权路径长度为( )。A、18
B、16
C、30
D、12
标准答案:A
-
第2题:
由分别带权9,2,3,5,6的五个叶子结点生成的哈夫曼树,该树的带权路径长度为
A.50
B.60
C.55
D.65
正确答案:C
解析:带权路径长度最小的二叉树叫哈夫曼树。先由哈夫曼算法生成哈夫曼树,有上述数据组成哈夫曼树,计算其带权路径(2+3)*3+(5+9+6)*2=55,所以本题正确答案为选项C。 -
第3题:
哈夫曼树又称为(),它是n个带权叶子结点构成的所有二叉树中带权路径长度WPL()。
最优二叉树;最小的二叉树
略 -
第4题:
霍夫曼树是带权路径长度最短的树,路径上权值较大的结点离根较近。
正确答案:正确 -
第5题:
由分别带权为3,9,6,2,5的共五个叶子结点构成一棵哈夫曼树,则带权路径长度为()
正确答案:55 -
第6题:
由带权为3,9,6,2,5的5个叶子结点构成一棵哈夫曼树,则带权路径长度为()。
正确答案:55 -
第7题:
树的带权路径长度为树中所有叶子结点的()。
正确答案:带权路径长度之和 -
第8题:
哈夫曼树是带权路径长度()的树,通常权值较大的结点离根结点()。
正确答案:最小;近 -
第9题:
问答题请解释结点的度、树的度、结点的层、树的深度、分支、路径、路径长度、树的路径长度、叶子结点、分支结点、内部结点、孩子、双亲、兄弟、堂兄弟、祖先、子孙、有序树、无序树和森林等基本术语的含义。正确答案: 结点的度和树的度:一个结点的后继的数目称为该结点的度,树中各结点度的最大值称为树的度。
结点的层和树的深度:树的根结点所在的层为第1层,其余结点的层等于其前驱结点的层加1,树中各结点的层的最大值称为树的深度。
分支、路径、路径长度和树的路径长度:从一个结点到其后继结点之间的连线称为一个分支,从一个结点X到另一个结点Y所经历的所有分支构成结点X到结点Y的路径,一条路径上的分支数目称为路径长度,从树的根结点到其他各个结点的路径长度之和称为树的路径长度。
叶子结点、分支结点和内部结点:树中度为0的结点称为叶子结点(或终端结点),度不为0的结点称为分支结点(或非终端结点),除根结点以外的分支结点也称为内部结点。
孩子和双亲:在树中,一个结点的后继结点称为该结点的孩子,相应地,一个结点的前驱结点称为该结点的双亲,即一个结点是其孩子结点的双亲、其双亲结点的孩子。
兄弟和堂兄弟:同一双亲的孩子结点之间互称为兄弟,不同双亲但在同一层的结点之间互称为堂兄弟。
祖先和子孙:从树的根结点到某一个结点X的路径上经历的所有结点(包括根结点但不包括结点X)称为结点X的祖先,以某一结点X为根的子树上的所有非根结点(即除结点X外)称为结点X的子孙。
有序树和无序树:对于树中的任一结点,如果其各棵子树的相对次序被用来表示数据之间的关系,即交换子树位置会改变树所表示的内容,则称该树为有序树;否则称为无序树。
森林:m(m≥0)棵互不相交的树的集合就构成了森林。解析: 暂无解析 -
第10题:
填空题哈夫曼树又称为(),它是n个带权叶子结点构成的所有二叉树中带权路径长度WPL()。正确答案: 最优二叉树,最小的二叉树解析: 暂无解析 -
第11题:
单选题对哈夫曼树,下列说法错误的是()。A哈夫曼树是一类带树路径长度最短的树
B给出一组数,构造的哈夫曼树唯一
C给出一组数,构造的哈夫曼树的带树路径长度不变
D哈夫曼树的带权路径长度为每个叶子的路径长度与该叶子权值乘积之和
正确答案: B解析: 暂无解析 -
第12题:
单选题由带权为9,2,5,7的四个叶子结点构造一棵哈夫曼树,该树的带权路径长度为()。A23
B37
C46
D44
正确答案: D解析: 暂无解析 -
第13题:
● 由权值为 29、12、15、6、23 的五个叶子结点构造的哈夫曼树为(64),其带权路径长度为 (65) 。

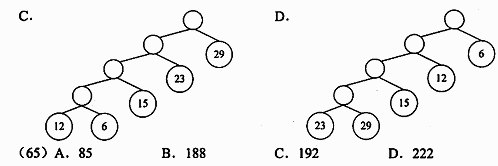 正确答案:A,B
正确答案:A,B
-
第14题:
由圈权值为9.2.5.7的四个叶子结点构造一颗哈夫曼树,该树的带权路径长度为()。A.23
B.37
C.44
D.46答案:C解析: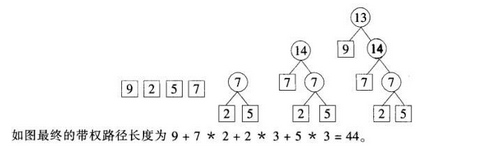
-
第15题:
树的带权路径长度最小的二叉树中必定没有度为1的结点。
正确答案:正确 -
第16题:
由带权为,9、2.5,7,的四个叶子结点构造一裸哈夫曼树.该树的带权路径长度为()。
正确答案:44 -
第17题:
山带权为3,6,2,5的5个叶子结点构成一裸哈夫爱树.则带权路径长度为()。
正确答案:55 -
第18题:
若以4,5,6,7,8作为叶子结点的权值构造哈夫曼树,则其带权路径长度是()。
正确答案:69 -
第19题:
请解释结点的度、树的度、结点的层、树的深度、分支、路径、路径长度、树的路径长度、叶子结点、分支结点、内部结点、孩子、双亲、兄弟、堂兄弟、祖先、子孙、有序树、无序树和森林等基本术语的含义。
正确答案:结点的度和树的度:一个结点的后继的数目称为该结点的度,树中各结点度的最大值称为树的度。
结点的层和树的深度:树的根结点所在的层为第1层,其余结点的层等于其前驱结点的层加1,树中各结点的层的最大值称为树的深度。
分支、路径、路径长度和树的路径长度:从一个结点到其后继结点之间的连线称为一个分支,从一个结点X到另一个结点Y所经历的所有分支构成结点X到结点Y的路径,一条路径上的分支数目称为路径长度,从树的根结点到其他各个结点的路径长度之和称为树的路径长度。
叶子结点、分支结点和内部结点:树中度为0的结点称为叶子结点(或终端结点),度不为0的结点称为分支结点(或非终端结点),除根结点以外的分支结点也称为内部结点。
孩子和双亲:在树中,一个结点的后继结点称为该结点的孩子,相应地,一个结点的前驱结点称为该结点的双亲,即一个结点是其孩子结点的双亲、其双亲结点的孩子。
兄弟和堂兄弟:同一双亲的孩子结点之间互称为兄弟,不同双亲但在同一层的结点之间互称为堂兄弟。
祖先和子孙:从树的根结点到某一个结点X的路径上经历的所有结点(包括根结点但不包括结点X)称为结点X的祖先,以某一结点X为根的子树上的所有非根结点(即除结点X外)称为结点X的子孙。
有序树和无序树:对于树中的任一结点,如果其各棵子树的相对次序被用来表示数据之间的关系,即交换子树位置会改变树所表示的内容,则称该树为有序树;否则称为无序树。
森林:m(m≥0)棵互不相交的树的集合就构成了森林。 -
第20题:
填空题山带权为3,6,2,5的5个叶子结点构成一裸哈夫爱树.则带权路径长度为()。正确答案: 55解析: 暂无解析 -
第21题:
填空题树的带权路径长度为树中所有叶子结点的()。正确答案: 带权路径长度之和解析: 暂无解析 -
第22题:
填空题由带权为,9、2.5,7,的四个叶子结点构造一裸哈夫曼树.该树的带权路径长度为()。正确答案: 44解析: 暂无解析 -
第23题:
单选题利用3、6、8、12这四个值作为叶子结点的权,生成一棵哈夫曼树,该树中所有叶子结点中的最长带权路径长度为()。A16
B30
C12
D18
正确答案: A解析: 暂无解析 -
第24题:
填空题由带权为3,9,6,2,5的5个叶子结点构成一棵哈夫曼树,则带权路径长度为()。正确答案: 55解析: 暂无解析
