itgle.com

若一直角三角形的周长与面积的数值相等，且两直角边长之和为14，则该三角形的面积是（ ）。A．20B．24C．12D．6.2 ( ⊙o⊙ )

题目

若一直角三角形的周长与面积的数值相等，且两直角边长之和为14，则该三角形的面积是（ ）。

A．20

B．24

C．12

D．6.2 ( ⊙o⊙ )

相似考题

1.若等腰直角三角形的直角边长为2，则以一直角边所在的直线为轴旋转一周所成的几何体体积是 。

2.用八个同样大小的等腰直角三角形拼成一个正方形，若三角形的面积为2平方厘米，那么正方形的周长是( ) 。A．8B．16C．20D．32

3.已知直角三角形两条直角边的和等于8，两条直角边各为多少时，这个直角三角形的面积最大，最大值是多少？

4.已知一直角三角形的一个直角边长为12，且周长比面积的数值小18，则该三角形的面积是：A．20B．36C．54D．96

更多“若一直角三角形的周长与面积的数值相等,且两直角边长之和为14,则该三角形的面积是( )。 ”相关问题

  • 第1题：

    已知一直角三角形的一个直角边长为12，且周长比面积的数值小18，则该三角形的面积是（ ）。

    A．20

    B．36 >>>>>

    C．54

    D．96


    正确答案：C

  • 第2题：

    直角三角形直角边长度平方之和等于斜边长度的平方，被称为（ ）。
    A.欧几里得定理 B.勾股定理
    C.阿基米德定律 D.黄金分割率


    答案：B
    解析：
    B [解析]略

  • 第3题：

    若一直角三角形的周长与面积的数值相等，且两直角边长之和为14，则该三角形的面积是（）。

    A.20
    B.24
    C.12
    D.6.2

    答案：B
    解析：
    两个直角边和为14，直角边中至少有一个大于等于7。根据斜边长度大于任意直角边，可知斜边大于7。则周长大于21。周长与面积相等，直接选B。

  • 第4题：

    如图9所示的“勾股树”中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大正方形的边长为12cm，则A、B、C、D四个小正方形的面积之和为__________。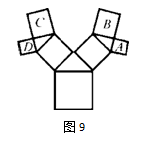


    答案：
    解析：
    144

  • 第5题：

    直角三角形两直角边长分别为60和80，则其斜边长应为120。


    正确答案:错误

  • 第6题：

    一个直角三角形，一条直角边长是1，另一条直角边长是2，它的面积就是2。


    正确答案:错误

  • 第7题：

    分别以直角三角形的三边为边向外作三个相似的多边形，则两直角边上的多边形的面积之和等于斜边上的多边形的面积。


    正确答案:错误

  • 第8题：

    一直角三角形两直角边分别为6mm、8mm，则其斜边长为（）。


    正确答案:10mm

  • 第9题：

    填空题
    若两个相似三角形的周长比为2∶3，则它们的面积比是____．

    正确答案： 4∶9
    解析：
    相似三角形的面积比是周长比的平方．

  • 第10题：

    填空题
    一直角三角形两直角边分别为6mm、8mm，则其斜边长为（）。

    正确答案： 10mm
    解析： 暂无解析

  • 第11题：

    单选题
    直角三角形的两直角边分别为4cm和5cm，直角三角形的面积是（）cm2。
    A

    5

    B

    10

    C

    15

    D

    20


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    下列说法正确的个数有（　　）。①等边三角形有三条对称轴；②在△ABC中，若a2＋b2≠c2，则△ABC不是直角三角形；③等腰三角形的一边长为4，另一边长9，则它的周长为17或22；④一个三角形中至少有两个锐角。
    A

    1个

    B

    2个

    C

    3个

    D

    4个


    正确答案： B
    解析：
    ①④正确。②中若a2＋b2≠c2，则△ABC也可能是直角三角形，如当∠A或∠B是直角；③若两边长为4，则4＋4＜9，不能构成三角形，故周长不能为17。

  • 第13题：

    若一个两边相等的三角形的两边长分别是4cm和9cm，则其周长是________.


    正确答案：
    22cm；

  • 第14题：

    如图，由四个全等的直角三角形拼成一个大正方形，每个三角形的面积都是1，且两直角边之比大于等于2，则这个大正方形的面积至少是()。

    A.4
    B.5
    C.6
    D.7

    答案：B
    解析：
    第一步，本题考查几何问题，属于平面几何类。
    第二步，根据图形可知大正方形面积＝4个三角形面积＋小正方形面积＝4＋小正方形面积，小正方形边长＝三角形长直角边－短直角边，那么当三角形两直角边差最小时，可得大正方形面积最小，由于两直角边之比大于等于2，即当两直角边之比等于2时，大正方形面积最小。
    第三步，设三角形短直角边为a，则长直角边为2a，三角形的面积为

    解得a＝1，所以小正方形的面积为（2a－a）2＝1×1＝1，故大正方形面积至少为4＋1＝5。
    因此，选择B选项。

  • 第15题：

    直角三角形的一条直角边长度等于斜边长度的一半,则它的外接圆面积与内切圆面积的比值为（ ）


    答案：E
    解析：

  • 第16题：

    直角边之和为12的直角三角形面积的最大值等于（）。

    • A、16
    • B、18
    • C、20
    • D、22
    • E、以上都不是

    正确答案:B

  • 第17题：

    有一个角为30度的直角三角形，较短的直角边长度是1，那么较长的直角边长度是多少？


    正确答案: 有一个角为30度的直角三角形，较短的直角边长度是1，那么较长的直角边长度是根号3。

  • 第18题：

    古希腊人发现根号二的存在主要是从（）的计算过程中发现的。

    • A、梯形面积
    • B、圆的面积
    • C、直角三角形边长
    • D、正方形边长

    正确答案:C

  • 第19题：

    直角三角形的两直角边分别为5cm和6cm，直角三角形的面积是（）cm²。

    • A、5
    • B、10
    • C、15
    • D、20

    正确答案:C

  • 第20题：

    分别在直角三角形三边向外作正五边形，则两直角边上的正五边形的面积之和等于斜边上的正五边形的面积。


    正确答案:正确

  • 第21题：

    单选题
    古希腊人发现根号二的存在主要是从（）的计算过程中发现的。
    A

    梯形面积

    B

    圆的面积

    C

    直角三角形边长

    D

    正方形边长


    正确答案： A
    解析： 暂无解析

  • 第22题：

    判断题
    分别以直角三角形的三边为边向外作三个相似的多边形，则两直角边上的多边形的面积之和等于斜边上的多边形的面积。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第23题：

    判断题
    分别在直角三角形三边向外作正五边形，则两直角边上的正五边形的面积之和等于斜边上的正五边形的面积。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

相关内容