itgle.com

甲、乙、丙、丁四个旅行团分别有游客69人、85人、93人、97人。现在要把这四个旅行团分别进行分组，使每组都是A名游客，以便乘车前往参观游览。已知甲、乙、丙三个旅行团分成每组A人的若干组后，所剩的人数都相同，问丁旅行团分成每组A人的若干组后还剩几人?A．0B．1C．2D．3

题目

甲、乙、丙、丁四个旅行团分别有游客69人、85人、93人、97人。现在要把这四个旅行团分别进行分组，使每组都是A名游客，以便乘车前往参观游览。已知甲、乙、丙三个旅行团分成每组A人的若干组后，所剩的人数都相同，问丁旅行团分成每组A人的若干组后还剩几人?

A．0

B．1

C．2

D．3

相似考题

1.填空： （1）一个长方形的宽为a cm，长比宽的2倍多25px，这个长方形的周长为________ _cm； （2）三个连续整数中，n是最小的一个，这三个数的和为_________ ； （3）某公园的成人票价是20元，儿童票价每张是8元。甲旅行团有x名成人和y名儿童；乙旅行团的成人数是甲旅行团的2倍，儿童数是甲旅行团的½。两个旅行团的门票费用总和为_____ ____元。

2.送乘搭飞机离站的旅行团，要待游客全部通过__________后，地陪方可离开；送乘搭火车、轮船离站的旅行团，要待游客全部通过__________ 后，地陪方可离开。

3.在四个域甲、乙、丙、丁，甲信任乙，乙信任丙，丙信任丁，甲信任丙，乙信任丁，则在丁中创建的全局组用户能访问域中的哪些资源()。A、甲、乙、丙、丁B、乙、丙、丁C、丙、丁D、丁

4.甲、乙、丙、丁比赛乒乓球，每两个人要赛一场，结果甲胜了丁，并且甲、乙、丙三人胜的场数相同。问丁胜了几场？A．0B．1C．2D．3

更多“甲、乙、丙、丁四个旅行团分别有游客69人、85人、93人、97人。现在要把这四个旅行团分别进行分组，使每组都是A名游客，以便乘车前往参观游览。已知甲、乙、丙三个旅行团分成每组A人的若干组后，所剩的人数都相同，问丁旅行团分成每组A人的若干组后还剩几人?A．0B．1C．2D．3”相关问题

  • 第1题：

    某厂有甲、乙、丙、丁四个车间，甲、乙两车间人数之比是9∶8,乙车间人数的5倍等于丙车间人数的4倍，丙车间人数的 等于丁车间人数的 ，如果丁车间工人数的8%退休以后还剩690人，那么甲车间有多少人?( )

    A.900                B.860             C.720            D.640


     .C【解析】因为乙车间人数的5倍等于丙车间人数的4倍，所以乙丙两车间人数之比是4∶5，同理，丙、丁两车间人数之比是 ∶ 又丁车间工人如果不退休，那么人数为690÷(1-8%)。设甲车间有x人，于是得x=720(人)

  • 第2题：

    某旅游公司有能载4名乘客的轿车和能载7名乘客的面包车若干辆，某日该公司将所有车辆分成车辆数相等的两个车队运送两支旅行团。已知两支旅行团共有79人，且每支车队都满载，问该公司轿车数量比面包车多多少辆（）

    A、5
    B、6
    C、7
    D、8

    答案：B
    解析：
    本题考查不定方程。解法一：设轿车x辆，面包车y辆。根据题意可知4x+7y=79，由奇偶性可知，7y必为奇数，则y必为奇数；同时根据条件可将车辆分成相等的两个车队，可知x+y为偶数，x-y必为偶数，排除AC，代入B，x-y=6，得x=11，y=5，完全符合题意。解法二：设轿车x辆，面包车y辆。根据题意可知4x+7y=79，由奇偶性可知，7y必为奇数，则y必为奇数；同时根据条件可将车辆分成相等的两个车队，可知x+y为偶数。当y=1时，x=18，x+y=19为奇数，与条件矛盾，排除；当y=3时，则x不为整数，排除；当y=5时，x=11，5+11=16为偶数，符合条件，该假设成立。则x-y=6。故本题答案为B选项。
    【知识点】不定方程（组）

  • 第3题：

    甲、乙、丙三个单位各派2名志愿者参加公益活动，现将这6人随机分成3组，每组2人，则每组成员均来自不同单位的概率是：

    A.2/3
    B.5/12
    C.7/4
    D.8/15

    答案：D
    解析：
    6个人随机分成3组，总数为C26×C24/A33=15种情况。每组成员来自不同的单位，正向考虑情况数较多，故反向考虑，即考虑每组成员来自相同的单位。
    第一类情况：只有一组来自同一单位。设甲1甲2同一单位，则剩下的两组可能有两种情况：乙1丙1和乙2丙2；乙1丙2和乙2丙1。满足的情况数为3×2=6种。
    第二类情况：有两组来自同一单位，而剩下一组也一定来自同一单位，即三组均来自同一单位，共1种情况。
    则满足每组成员来自相同单位的概率=6+1/15=7/15，所求每组成员均来自不同单位的概率P=1-7/15=8/15。
    故正确答案为D。

  • 第4题：

    一群大学生进行分组活动，要求每组人数相同，若每组22人，则多出一人未分进组；若少分一组，则恰好每组人数一样多，已知每组人数最多只能32人，则该群学生总人数是（ ）

    A．441 B．529 C．536 D．528

    答案：B
    解析：
    。解法一：由题干“每组22人，则多出一人未分进组”可知，学生总人数减去1后可以被22整除。C、D两项的数字减去1后均为奇数，无法被22整除，排除。代入A项，441－1=22×20，但是441无法被19整除，排除。验证B项符合题意，当选。
    解法二：第二次少分一组，说明把多出的22+1=23（人）平均分给了第二次各组。由23是质数，可知第二次总组数只能为23，则第一次分了24组，总人数为24×22+1，利用尾数法算得尾数为9，B项符合。

  • 第5题：

    某项活动中，将3男3女6名志愿者随机地分成甲、乙、丙三组，每组2人，则每组志愿者都是异性的概率为

    A.1/90
    B.1/15
    C.1/10
    D.1/5
    E.2/5

    答案：E
    解析：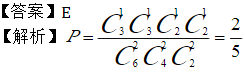

  • 第6题：

    单选题
    甲、乙、丙三个旅行团的游客人数都相等，且每个游客的平均年龄都是32岁，这三个团游客年龄的方差分别是S甲2＝27，S乙2＝19.6，S丙2＝1.6．导游小王最喜欢带游客年龄相近的团队，若在这三个团中选择一个，则他应选（　　）．
    A

    甲团

    B

    乙团

    C

    丙团

    D

    甲团或乙团


    正确答案： D
    解析：
    三组数据中，丙团游客年龄的方差最小，表明丙团游客年龄的波动最小，年龄最接近．

  • 第7题：

    单选题
    甲、乙、丙、丁四个旅行团分别有游客69人、85人、93人、97人。现在要把这四个旅行团分别进行分组，使每组都是A名游客，以便乘车前往参观游览。已知甲、乙、丙三个旅行团分成每组A人的若干组后，所剩的人数都相同，问丁旅行团分成每组A人的若干组后还剩几人？（）
    A

    0

    B

    1

    C

    2

    D

    3


    正确答案： D
    解析： 暂无解析

  • 第8题：

    甲、乙、丙、丁在比他们的身高。甲说：“我最高。”乙说：“我不是最矮的。”丙说：“我没甲高，但还有人比我矮。”丁说：“我可能最矮。”实际测量的结果表明，只有一人说错了。

    这四个人从高到低的排列是( )。

    A.甲、乙、丙、丁

    B．乙、丙、甲、丁

    C．乙、甲、丙、丁

    D．甲、乙、丁、丙


    正确答案：C

  • 第9题：

    某旅行团共有48名游客，都报名参观了三个景点中的至少一个。其中，只参观了一个景点的人数与至少参观了两个景点的人数相同，是参观了三个景点的人数的4倍。则需要为这些游客购买多少张景点门票？

    A.48
    B.72
    C.78
    D.84

    答案：C
    解析：
    根据题意，只参观一个景点的人数与至少参观了两个景点的人数相同，都为48÷2=24，则 参观了三个景点的人数为24÷4=6,只参观两个景点的人数为24-6=18,则共需购买24+18x2+6x3=78张景点门票。

  • 第10题：

    已知有甲、乙、丙、丁四个数，甲、乙之和大于丙、丁之和，甲、丁之和大于乙、丙之和，乙、丁之和大于甲、丙之和。根根据以上请判断这四个数谁最小？（）
    A 甲最小
    B 丙最小
    C 乙最小
    D 丁最小


    答案：B
    解析：
    第一步：整理题干信息。
    （1）甲＋乙>丙＋丁；（2）甲＋丁>乙＋丙；（3）乙＋丁>甲＋丙。
    第二步：根据信息整合。
    将不等式相加，同方向的不等号不变，（1）+（2）可得甲>丙，（2）+（3）可得丁>丙，（1）+（3）可得乙>丙，综合三个结果可知丙最小。
    故正确答案为B。

  • 第11题：

    甲、乙、丙、丁4个足球队参加比赛,假设每场比赛各队取胜的概率相等,现任意将这4个队分成两个组（每组两个队）进行比赛,胜者再赛,则甲、乙相遇的概率为（ ）

    A.1/6
    B.1/4
    C.1/5
    D.1/3
    E.1/2

    答案：E
    解析：

  • 第12题：

    现场勘查工作的一般做法步骤是（） 甲：组织人员进行清查 乙：确定财产的成新率 丙：利用细分法，将财产分成若干部份 丁：对各部分财产进行技术鉴定

    • A、甲→乙→丙→丁
    • B、甲→丙→乙→丁
    • C、丙→乙→甲→丁
    • D、甲→丙→丁→乙

    正确答案:D

  • 第13题：

    单选题
    现场勘查工作的一般做法步骤是（） 甲：组织人员进行清查 乙：确定财产的成新率 丙：利用细分法，将财产分成若干部份 丁：对各部分财产进行技术鉴定
    A

    甲→乙→丙→丁

    B

    甲→丙→乙→丁

    C

    丙→乙→甲→丁

    D

    甲→丙→丁→乙


    正确答案： A
    解析： 暂无解析

  • 第14题：

    单选题
    已知有甲、乙、丙、丁四个数，甲乙之和大于丙丁之和，甲丁之和大于乙丙之和，乙丁之和大于甲丙之和。根据以上请判断这四个数谁最小？（　　）
    A

    甲最小

    B

    丙最小

    C

    乙最小

    D

    丁最小


    正确答案： B
    解析：
    由题可知：①甲＋乙＞丙＋丁；②甲＋丁＞乙＋丙；③乙＋丁＞甲＋丙。由①＋②可推知甲＞丙，由①＋③可推知乙＞丙，由②＋③可推知丁＞丙，即丙最小。因此B项正确。

相关内容