举例给出一个十进制正数X1，一个十进制负数Y1，写出： （1）X1和Y1的十进制真值； （2）X1和Y1的二进制真值； （3）X1和Y1的原码、反码和补码； （4）用8位二进制补码分别计算X1+Y1, X1-Y1，结果用十进制数表示。

将十进制数一 0.276和47化成二进制数，再写出各自的原码、反码、补码表示(符号位和数值位共8位)。

二进制数11001100为原码的时候，它代表的真值为(7)；若它是补码，则它代表的真值为(8)；十进制数-1的补码用8位二进制数表示为(9)

A．204

B．-76

C．-204

D．76

二进制数11001100为原码时，代表的真值为(7)；若它是补码，而代表的真值为(8)，十进制-1的补码用8位二进制表示为(9)。

A．204

B．-76

C．-204

D．76

A.越小

B.越大

C.平均

D.相等

用十六位机器码1110001010000000来表示定点整数(最高位为符号位)，当它是原码时表示的十进制真值为(1)。当它是补码时表示的十进制真值是(2)；当它是反码时表示的十进制真值是(3)。

A．-12608

B．-7551

C．-7552

D．-25216

阅读以下说明和c++代码，将应填入(n)处的字句写在对应栏内。

【说明】

现要编写一个画矩形的程序，目前有两个画图程序：DP1和DP2，DP1用函数draw_a_line(x1， y1，x2，y2)画一条直线，DF2则用drawline(x1，x2，y1，y2)画一条直线。当实例画矩形时，确定使用DP1还是DP2。为了适应变化，包括“不同类型的形状”和“不同类型的画图程序”，将抽象部分与实现部分分离，使它们可以独立地变化。这里，“抽象部分”对应“形状”，“实现 部分”对应“画图”，与一般的接口(抽象方法)与具体实现不同。这种应用称为Bridge(桥接)模式。图9-7显示了各个类间的关系。

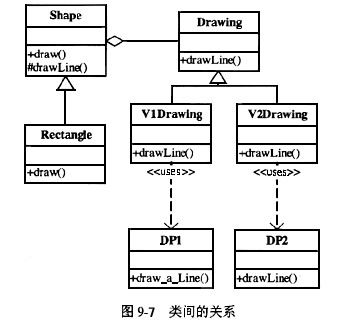
这样，系统始终只处理3个对象：Shape对象、Drawing对象、DP1或DP2对象。以下是 C++语言实现，能够正确编译通过。

【C++代码】

class DP1{

public:

static void draw_a_line(double x1, double y1,double x2, double y2){

//省略具体实现

}

);

class DP2{

public:

static void drawline(double x1, double x2,double y1, double y2){

//省略具体实现

}

};

class Drawing{

public:

(1) void drawLine(double x1,double y1,double x2,double y2)=0;

};

class V1Drawing:public Drawing{

public:

void drawLine(double x1, double y1,double x2, double y2){

DP1::draw_a_line(x1,y1,x2,y2);

}

};

class V2Drawing:public Drawing{

public:

void drawLine(double x1, double y1, double x2, double y2){

(2);

}

};

class Shape{

private:

(3) _dp;

public:

Shape(Drawing *dp);

virtual void draw()=0;

void drawLine(double x1, double y1, double x2, double y2);

};

Shape::Shape(Drawing *dp)

{

_dp = dp;

}

void Shape::drawLine(double x1, double y1, double x2, double y2)

{ //画一条直线

(4);

}

class Rectangle: public Shape{

private:

double _x1,_y1,_x2,_y2;

public:

Rectangle(Drawing *dp, double x1, double y1,

double x2, double y2);

void draw();

};

Rectangle::Rectangle(Drawing *dp, double x1, double y1, double x2, double y2)

:(5)

{

_x1=x1;_y1=y1;_x2=x2;_y2=y2;

}

void Rectangle::draw()

{

//省略具体实现

}