试分别叙述罗尔中值定理和拉格朗日中值定理。若以S(x)记由(a,(a)),(b,(b)),(x,(x)))三点组成的三角形面积,试对S(x)应用罗尔中值定理证明拉格朗日中值定理。
题目
试分别叙述罗尔中值定理和拉格朗日中值定理。若以S(x)记由(a,(a)),(b,(b)),(x,(x)))三点组成的三角形面积,试对S(x)应用罗尔中值定理证明拉格朗日中值定理。
相似考题
参考答案和解析
答案:
解析:
罗尔中值定理:若函数(x)满足如下条件: (1)(x)在闭区间[a,b]上连续;
(2)(x)在开区间(a,b)内可导;
(3)(a)=(b),
则在(a,b)内至少存在一点ξ,使得’(ξ)=0。
拉格朗日中值定理:若函数(x)满足如下条件:
(1)(x)在闭区间[a,b]上连续;
(2)(x)在开区间(a,b)内可导,
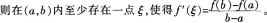
在xOy面上考虑,记由A(a,(a),0),B(b,(b),0),C(x,(x),0)三点组成的三角形面积S(x),则

(2)(x)在开区间(a,b)内可导;
(3)(a)=(b),
则在(a,b)内至少存在一点ξ,使得’(ξ)=0。
拉格朗日中值定理:若函数(x)满足如下条件:
(1)(x)在闭区间[a,b]上连续;
(2)(x)在开区间(a,b)内可导,
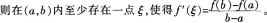
在xOy面上考虑,记由A(a,(a),0),B(b,(b),0),C(x,(x),0)三点组成的三角形面积S(x),则

更多“试分别叙述罗尔中值定理和拉格朗日中值定理。若以S(x)记由(a,(a)),(b,(b)),(x,(x)))三点组成的三角形面积,试对S(x)应用罗尔中值定理证明拉格朗日中值定理。”相关问题
-
第1题:
设x、y和z是int型变量,且x=4,y=6,z=8,则下列表达式中值为0的是()。A.x&&yB.x<=yC.x‖y+z&am设x、y和z是int型变量,且x=4,y=6,z=8,则下列表达式中值为0的是( )。
A.x&&y
B.x<=y
C.x‖y+z&&y-z
D.!((x<y)&&!z‖1)
正确答案:D
解析:本题考查逻辑运算符的使用。当“&&”的两个运算对象都是逻辑1时,表达式才返回值是1;当“‖”的两个运算对象至少有一个是逻辑1时,表达式返回值是1。选项A)中,x和y都是逻辑1,所以返回值是1;选项B)中,x=4=y=6为逻辑1,所以返回值是1;选项C中,y+z的值等于14,非0,y-z的值为-2,非0,所以逻辑表达式4‖14&&-2的值不为0;选项D)中,xy为1,!z为0,1&&0为1,0‖1为1,因此,!1为0。 -
第2题:
设x、y和z是int型变量,且x=4,y=6,z=8,则下列表达式中值为0的是( )。A.x&&y B.x<=y S设x、y和z是int型变量,且x=4,y=6,z=8,则下列表达式中值为0的是( )。
A.x&&y
B.x<=y
C.x||y+z&&y-z
D.!((x<y)&&!z||1)
正确答案:D
本题考查逻辑运算符的使用。当“&&”的两个运算对象都是逻辑1时,表达式返回值才是1;“||”的两个运算对象至少有一个是逻辑1时,表达式返回值也是1,x<y为1,!z为0,1&&0为1,0||为1,因此,!1为0。 -
第3题:
设数列{an}满足条件:a0=3,a1=1,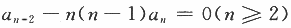 ,S(x)是幂级数
,S(x)是幂级数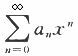 的和函数.
的和函数.
(Ⅰ)证明:S"(x)-S(x)=0;
(Ⅱ)求S(x)的表达式.答案:解析:【分析】利用幂级数可逐项求导的性质,验证(Ⅰ)成立;解微分方程求出S(x),注意初值条件的使用.

-
第4题:
质量为2k9的物体,在沿x方向的变力作用下,在x=0处由静止开始运动。设变力与x的关系如图所示。试由动能定理求物体在x=5,10,15m处的速率。
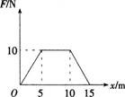 答案:解析:
答案:解析: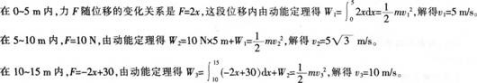
-
第5题:
叙述并证明拉格朗日微分中值定理,并简述拉格朗日微分中值定理与中学数学内容的联系。答案:解析:本题主要考查微分中值定理中十分重要的拉格朗日中值定理。
证明拉格朗日微分中值定理,首先要从罗尔定理出发,
-
第6题:
函数y=sinx在区间[0,π]上满足罗尔定理的ξ=( ) 答案:C解析:
答案:C解析: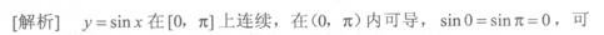
-
第7题:
函数y=cosx在[0,2x]上满足罗尔定理,则ξ= .答案:解析:【答案】π【考情点拨】本题考查了罗尔定理的知识点.
【应试指导】
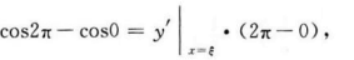

-
第8题:
在特殊要素模型中,试讨论以下定理是否继续成立:(1)斯托尔珀-萨缪尔逊定理(2)罗勃津斯基定理。
正确答案:(1)只对特定要素成立。在特殊要素模型中,一种产品价格的增加会使该产品使用的特定要素的价格增加,而使另一种产品使用的特定要素价格下降,公共要素价格的变动不确定。
(2)只对特定要素成立。因为特定要素的增加会使使用该要素的产品的产量增加,而使另一种产品的产量下降,但是公共要素的增加就会使两种产品的产量都增加。 -
第9题:
下列是对称的数学公式的是()。
- A、欧拉函数
- B、薛定谔方程式
- C、拉格朗日中值定理
- D、海伦公式
正确答案:D -
第10题:
判断题当x趋近∞时,素数定理渐近等价于π(x)~Li(x)。A对
B错
正确答案: 错解析: 暂无解析 -
第11题:
填空题设线性链表的存储结构如下: struct node {ELEMTP data; /*数据域*/ struct node *next; /*指针域*/ } 试完成下列在链表中值为x的结点前插入一个值为y的新结点。如果x值不存在,则把新结点插在表尾的算法。 void inserty(struct node *head,ELEMTP x,ELEMTP y) {s=(struct node *)malloc(sizeof(struct node)); (); if(){s->nexr=head;head=s;} else { q=head;p=q->next; while(p->dqta!=x&&p->next!=NULL){q=p;()} if(p->data= = x){q->next=s;s->next=p;} else{p->next=s;s->next=NULL;} } }正确答案: s->data=y,head->data= =x,p=p->next解析: 暂无解析 -
第12题:
问答题设f(x)在闭区间[0,c]上连续,其导数f′(x)在开区间(0,c)内存在且单调减少,f(0)=0,试应用拉格朗日中值定理证明不等式:f(a+b)≤f(a)+f(b),其中a,b满足条件0≤a≤b≤a+b≤c。正确答案:
f(a+b)-f(a)-f(b)=[f(a+b)-f(b)]-[f(a)-f(0)]。
因为f(x)在区间(0,a),(b,a+b)上满足拉格朗日中值定理,因此分别存在ξ∈(0,a),η∈(b,a+b),使得f(a)-f(0)=af′(ξ),f(a+b)-f(b)=af′(η),从而有f(a+b)-f(a)-f(b)=a[f′(η)-f′(ξ)]。
又f′(x)在(0,c)上单调减少,故f′(η)≤f′(ξ),故f(a+b)-f(a)-f(b)≤0,即f(a+b)≤f(a)+f(b)。解析: 暂无解析 -
第13题:
设x、y和z是int型变量,且x=4,y=6,z=8,则下列表达式中值为0的是( )。A.x&&yB.x<=y设x、y和z是int型变量,且x=4,y=6,z=8,则下列表达式中值为0的是( )。
A.x&&y
B.x<=y
C. x||++y&&y-z
D.!(x
正确答案:D
本题考查逻辑运算符的使用。当“&&”的两个运算对象都是逻辑1时,表达式返回值才是1;“||”的两个运算对象至少有一个是逻辑1时,表达式返回值也是1,x<y为1,!z为0,1&&0为1,0||为1,因此,!1为0。 -
第14题:
在区间[0,8]上,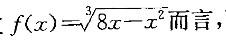 下列中哪个结论是正确的?
下列中哪个结论是正确的?
A.罗尔定理不成立 B.罗尔定理成立,且ζ=2
C.罗尔定理成立,且ζ=4 D.罗尔定理成立,且ζ=8答案:C解析:提示:验证函数是否满足罗尔定理的条件,利用罗尔定理结论求出ζ值如下。
f(x)在[0,8]上连续,在(0,8)内可导,且f(0)=f(8)=0,利用罗尔定理,在(0,8)之间至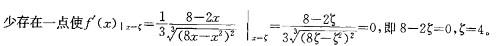
-
第15题:
(Ⅰ)证明拉格朗日中值定理:若函数f(x)在[a,b]上连续,在(a,b)内可导,则存在ξ∈(a,b),使得f(b)-f(a)=f'(ξ)(b-a);(Ⅱ)证明:若函数f(x)在x=0处连续,在(0,δ)(δ>0)内可导,且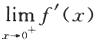 =A,则
=A,则 存在,且.
存在,且.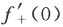 答案:解析:
答案:解析:

-
第16题:
叙述并证明拉格朗日微分中值定理,并简述拉格朗日中值定理与中学数学内容的联系。答案:解析:
-
第17题:
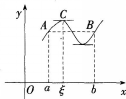
罗尔定理:设函数(x)满足条件:(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;(3)(a)=(b),则在(a,b)内至少存在一点ξ,使得,′(ξ)=0。证明这个定理并说明其几何意义。答案:解析:
-
第18题:
函数y=x2-x+1在区间[-1,3]上满足拉格朗日中值定理的ξ=( ) 答案:D解析:y=x2-x+1在[-1,3]上满足拉格朗日中值定理,
答案:D解析:y=x2-x+1在[-1,3]上满足拉格朗日中值定理,
-
第19题:
中值选民定理
正确答案:一个数学结论,表明如果要选民沿着一条线选一个点,而且,每个选民都想选离他最偏好的点最近的点,那么,多数原则将选出中值选民最偏好的点。 -
第20题:
证明不完全性定理的人是()
- A、伽罗瓦
- B、伯奈斯
- C、哥德尔
- D、爱因斯坦
正确答案:C -
第21题:
问答题在特殊要素模型中,试讨论以下定理是否继续成立:(1)斯托尔珀-萨缪尔逊定理(2)罗勃津斯基定理。正确答案: (1)只对特定要素成立。在特殊要素模型中,一种产品价格的增加会使该产品使用的特定要素的价格增加,而使另一种产品使用的特定要素价格下降,公共要素价格的变动不确定。
(2)只对特定要素成立。因为特定要素的增加会使使用该要素的产品的产量增加,而使另一种产品的产量下降,但是公共要素的增加就会使两种产品的产量都增加。解析: 暂无解析 -
第22题:
单选题下列是对称的数学公式的是()。A欧拉函数
B薛定谔方程式
C拉格朗日中值定理
D海伦公式
正确答案: D解析: 暂无解析 -
第23题:
单选题证明不完全性定理的人是()A伽罗瓦
B伯奈斯
C哥德尔
D爱因斯坦
正确答案: A解析: 暂无解析
