itgle.com

二元多项式f（x1,x2)，如果将x1，x2对换后，有f(x1,x2=f(x2,x1)则称f（x1,x2）为二元对称多项式。下列是二元对称多项式的是( )。 A． B． C． D．

题目
二元多项式f（x1,x2)，如果将x1，x2对换后，有f(x1,x2=f(x2,x1)则称f（x1,x2）为二元对称多项式。下列是二元对称多项式的是( )。
A．
B．
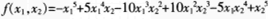
C．
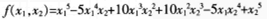
D．

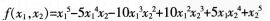
相似考题

1.已知x1(t)和x2(t)的傅里叶变换分别为X1(f)和X2(f),则卷积x1(t)*x2(t)的傅里叶变换为()。A、X1(f)X2(f)B、X1(f)*X2(f)C、X1(-f)X2(-f)D、X1(-f)*X2(-f)

2.关于随机变量特征数的表达式不正确的是( )。A．E(aX+b)＝aE(X)+bB．F(X1+X2)＝E(X1)+E(X2)C．var(X1±X2)=var(X1)+var(X2)D．var(aX+b)＝avar(X)

3.一个队列的入队序列是a,b,x1,x2,c,d,则队列的出队序列是()。A、a，b，x1，x2，c，dB、x2，x1，d，c，b，aC、a，d，x2，x1，c，bD、x1，x2，c，d，a，b

4.如果用某布尔代数表达式F(X1，，X2，…，Xn)表示全集中的某个取值，则称其为（ ）。

更多“二元多项式f（x1,x2)，如果将x1，x2对换后，有f(x1,x2=f(x2,x1)则称f（x1,x2）为二元对称多项式。下列是二元对称多项式的是( )。 ”相关问题

  • 第1题：

    设数据x1，x2的绝对误差限分别为0.05和0.005，那么两数的乘积x1x2的绝对误差限E(x1x2)=

    A、0.005|X2|+0.005|X1|

    B、0.05|X2|+0.005|X1|

    C、0.05|X1|+0.005|X2|

    D、0.005|X1|+0.005|X2|


    参考答案：B

  • 第2题：

    如果F实现一个程序，输入变量x1和x2的边界、区间分别为：a≤x1≤d，区间为[a,b],[b,c],[c,d]；e≤x2≤g，区间为[e,f],[f,g]；则下列_ d_图可表示为强健壮等价类测试用例。

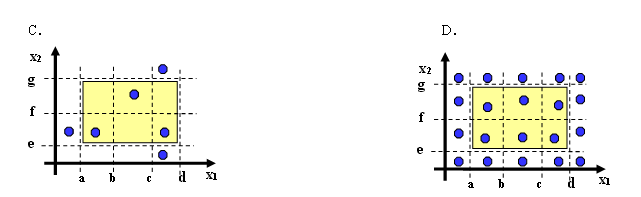
    A.A

    B.B

    C.C

    D.D


    正确答案：D

  • 第3题：

    已知函数f(x)=(a+1)lnx+ax2+1.

    (Ⅰ)讨论函数f(x)的单调性；

    (Ⅱ)设a≤-2，证明：对任意x2,x2 (0,+∞)，|f(x1)-f(x2)|≥4|x1-x2|.


    正确答案：


  • 第4题：

    设X1,X2,…Xn是简单随机样本，则有（ ）。
    A. X1,X2,…Xn相互独立 B. X1,X2,…Xn有相同分布
    C. X1,X2,…Xn彼此相等 D.X1与(X1,+X2)/2同分布
    E.X1与Xn的均值相等


    答案：A,B,E
    解析：
    简单随机样本满足随机性和独立性，且每一个样本都与总体同分布，样本均值相等。

  • 第5题：

    二次型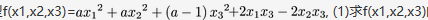, (1)求f(x1,x2,x3)的矩阵的特征值. (2)设f(x1,x2,x3)的规范形为. 求a


    答案：
    解析：

  • 第6题：

    设f(x)处处连续，且在x=x1处有f'(x1)=0,在x=x2处不可导，那么（ ）。
    A.x=x1及x=x2都必不是f(x)的极值点
    B.只有x=x1是f(x)的极值点
    C.x=x1及x=x2都有可能是f(x)的极值点
    D.只有x=x2是f(x)的极值点


    答案：C
    解析：
    提示：驻点和导数不存在点都是极值可疑点。

  • 第7题：

    映射f：A→B，若A中任意两个不同元素x1≠x2有f（x1）≠f（x2），则f是（）。

    • A、单射
    • B、满射
    • C、双射
    • D、反射

    正确答案:A

  • 第8题：

    设f（x）处处连续，且在x=x1处有f＇（x1）=0，在x=x2处不可导，那么（）。

    • A、x=x1及x=x2都必不是f（x）的极值点
    • B、只有x=x1是f（x）的极值点
    • C、x=x1及x=x2都有可能是f（x）的极值点
    • D、只有x=x2是f（x）的极值点

    正确答案:C

  • 第9题：

    填空题
    已知P（X＞x1）＝0.5，P（X≤x2）＝0.6，则x1（）x2。

    正确答案： ＜
    解析： 暂无解析

  • 第10题：

    多选题
    下列结论正确的是（）
    A

    P（x1≤ξ≤x2）=F（x2）-F（x1）

    B

    （-x）=1-Φ（x）

    C

    P（AB）=P（A）P（B）

    D

    P（A+B）=P（A）+P（B）


    正确答案： D,B
    解析： 暂无解析

  • 第11题：

    单选题
    设f（x）在（－∞，＋∞）内可导，且对任意x2＞x1，都有f（x2）＞f（x1），则正确的结论是（　　）。
    A

    对任意x，f′（x）＞0

    B

    对任意x，f′（x）≤0

    C

    函数－f（－x）单调增加

    D

    函数f（－x）单调增加


    正确答案： A
    解析：
    令F（x）＝－f（－x），由题知x2＞x1，则－x2＜－x1，则有f（－x2）＜f（－x1），即－f（－x2）＞－f（－x1），即F（x2）＞F（x1）单调增加，C正确。取f（x）＝x3，可排除A项。取f（x）＝x，可排除B、D项。

  • 第12题：

    单选题
    映射f：A→B，若A中任意两个不同元素x1≠x2有f（x1）≠f（x2），则f是（）。
    A

    单射

    B

    满射

    C

    双射

    D

    反射


    正确答案： B
    解析： 暂无解析

  • 第13题：

    请补充main函数，该函数的功能是求方程ax2+bx+c=0的根(方程的系数a,b,c从键盘输入)。

    例如， 当a=1，b=2，c=1时， 方程的两个根分别是：

    x1=-1.00,x2=-1.00。

    注意：部分源程序给出如下。

    请勿改动主函数main和其他函数中的任何内容，仅在 main函数的横线上填入所编写的若干表达式或语句。

    试题程序：

    include ＜stdio.h＞

    include ＜conio.h＞

    include ＜math.h＞

    main()

    {

    float a，b，c，disc，x1，x2，p，q；

    scanf("%f，%f，%f"，&a，&b，&c)；

    disc=b*b-4*a*c；

    clrscr()；

    printf("****** the result ****+*+\n")；

    if(disc＞=0)

    {

    x1=【 】；

    x2=(-b-sqrt(disc))/(2*a)；

    printf("x1=%6．2f，x2=%6.2f\n"，x1，x2)；

    }

    else

    {

    p=【 】；

    q=【 】；

    printf("x1=%6.2f+%6.2f i\n"，p，q)；

    printf("x2=%6.2f-%6.2f i\n"，p，q)；

    }

    }


    正确答案：(-b+sqrq(disc))/(2*a) -b/(2*a) sqrt(fabs(disc))/(2*a)
    (-b+sqrq(disc))/(2*a) -b/(2*a) sqrt(fabs(disc))/(2*a) 解析：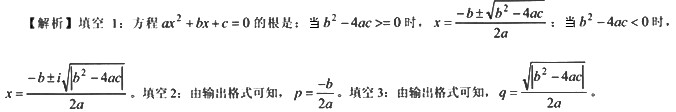

  • 第14题：

    一个关系模式为Y(X1,X2,X3,X4)，假定该关系存在函数依赖：(X1,X2)→X3，X2→X4，则该关系的码为______。

    A．X1

    B．X2

    C．(X1，X2)

    D．(X1,X2,X3,X4)


    正确答案：C

  • 第15题：

    已知样本x1,x2,…,xn，其中μ未知。下列表达式中，不是统计量的是（）。
    A. X1 +X2 B. max(x1,x2,…,xn)
    C. X1 +X2 -2μ D. (X1 -μ)/σ
    E. X1 +μ


    答案：C,D,E
    解析：
    不含未知参数的样本函数称为统计量。CDE三项都含有未知数μ，不是统计量。

  • 第16题：

    已知二次型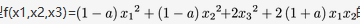的秩为2.(1)求a.(2)求作正交变换X=QY,把f(x1,x2,x3)化为标准形.(3)求方程f(x1,x2,x3)=0的解


    答案：
    解析：

  • 第17题：

    王小姐以固定的比例消费X1和X2，她每次消费1单位的X2就要消费2单位的X1，则以下哪一个效用函数可表示她的偏好？( )

    A.U(X1,X2) =2X1+X2
    B.U(X1,X2) =X1+2X2
    C.U(X1,X2) =min{2X1,X2)
    D.U(X1,X2) =min{X1,2X2)

    答案：D
    解析：
    由于王小姐以固定的比例消费X1和X2两种商品，所以X1和X2互为互补品。消费1单位的X2需要2单位的X1，则其效用函数为u(X1，X2) =min{X1，2X2}。

  • 第18题：

    同一条输电线三序电抗X1，X2，X0的大小关系是（）。

    • A、X1＞X2＞X0
    • B、X1=X2＞X0
    • C、X1=X2＜X0
    • D、X2＞1＞X0

    正确答案:C

  • 第19题：

    下列结论正确的是（）

    • A、P（x1≤ξ≤x2）=F（x2）-F（x1）
    • B、（-x）=1-Φ（x）
    • C、P（AB）=P（A）P（B）
    • D、P（A+B）=P（A）+P（B）

    正确答案:A,B

  • 第20题：

    已知P（X＞x1）＝0.5，P（X≤x2）＝0.6，则x1（）x2。


    正确答案:＜

  • 第21题：

    单选题
    若函数f（x）在区间（a，b）内可导，x1和x2是区间（a，b）内任意两点（x1＜x2），则至少存在一点ξ，使（　　）
    A

    f（b）－f（a）＝f′（ξ）（b－a）（a＜ξ＜b）

    B

    f（b）－f（x1）＝f′（ξ）（b－x1）（x1＜ξ＜b）

    C

    f（x2）－f（x1）＝f′（ξ）（x2－x1）（x1＜ξ＜x2）

    D

    f（x2）－f（a）＝f′（ξ）（x2－a）（a＜ξ＜x2）


    正确答案： C
    解析：
    考查拉格朗日中值定理的应用。
    值得注意的是，当函数f（x）在[a，b]上连续且在（a，b）内可导时，才可在[a，b]上对函数f（x）应用拉格朗日中值定理。
    由于题中没有说明函数f（x）在[a，b]上连续，因此有可能f（x）在x＝a或x＝b上没有定义，选项中涉及f（a）、f（b）的均为错误选项。

  • 第22题：

    问答题
    设f（x）在（a，b）内二阶可导，且f″（x）≥0，证明：对于（a，b）内任意两点x1、x2及0≤t≤1，有f[（1－t）x1＋tx2]≤（1－t）f（x1）＋tf（x2）。

    正确答案：
    由于不等式中含有f[(1-t)x1+tx2]、f(x1)、f(x2),则应在x0=(1-t)x1+tx2处展开泰勒式,即f(x)=f(x0)+f′(x0)(x-x0)+f″(ξ)(x-x0)2/(2!),ξ介于x和x0之间。
    又f″(x)≥0,则f″(ξ)≥0。故f(x)≥f(x0)+f′(x0)(x-x0)。则
    f(x1)≥f(x0)+f′(x0)(x1-x0)①
    f(x2)≥f(x0)+f′(x0)(x2-x0)②
    ①(1-t)+②t,得(1-t)f(x1)+tf(x2)≥f(x0)+f′(x0)[(1-t)x1+tx2-x0]=f(x0),即(1-t)f(x1)+tf(x2)≥f[(1-t)x1+tx2]。
    解析： 暂无解析

  • 第23题：

    问答题
    设函数f（x）在（a，b）内连续，a＜x1＜x2＜…＜xn＜b，证明：必∃ξ∈（a，b），使f（ξ）＝[f（x1）＋f（x2）＋…＋f（xn）]/n。

    正确答案：
    设f(x)在[x1,xn]上的最大值为M,最小值为m。
    则由题设可知,f(x)在[x1,xn]上连续,则它在[x1,xn]上必有最大值和最小值,则m≤[f(x1)+f(x2)+…+f(xn)]/n≤M。
    由最值介值定理可知,必∃ξ∈[x1,xn]⊂(a,b),使得f(ξ)=[f(x1)+f(x2)+…+f(xn)]/n。
    解析： 暂无解析

相关内容