itgle.com

袋子中有70个红球，30个黑球，从袋子中连续摸球两次，每次摸一个球，且第一次摸出的球，不放回袋中： (1)求两次摸球均为红球的概率： (2)若第一次摸到红球，求第二次摸到黑球的概率。

题目
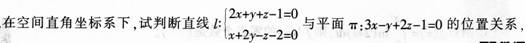
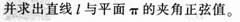袋子中有70个红球，30个黑球，从袋子中连续摸球两次，每次摸一个球，且第一次摸出的球，不放回袋中：
(1)求两次摸球均为红球的概率：
(2)若第一次摸到红球，求第二次摸到黑球的概率。

相似考题

1.一个袋内有100个球，其中有红球28个、绿球20个、黄球12个、蓝球20个、白球10个、黑球10个。现在从袋中任意摸球出来，如果要使摸出的球中，至少有15个球的颜色相同，问至少要摸出几个球才能保证满足上述要求?（ ）A．78B．77C．75D．68

2.一个袋子中有5只黑球3只白球,从袋中任取两只球,若以A表示:“取到的两只球均为白球”;B表示:“取到的两只球同色”。则P(A)=();P(B)=()。

3.一个口袋中装有3个一样的球，3个球上分别写有数字2，3和4。若第一次从袋子中取出一个球，记下球上的数字A，并将球放回袋中。第二次又从袋子中取出一个球，记下球上的数字B，然后算出它们的积。则所有不同取球情况所得到的积的和是。A．52B．56C．75D．81

4.（本小题满分12分）袋中有大小、形状相同的红、黑球各一个，现一次有放回地随机摸取3次，每次摸取一个球（Ⅰ）试问：一共有多少种不同的结果？请列出所有可能的结果；

更多“袋子中有70个红球，30个黑球，从袋子中连续摸球两次，每次摸一个球，且第一次摸出的球，不放回袋中： ”相关问题

  • 第1题：

    某商店搞店庆，购物满198元可以抽奖一次。一个袋中装有编号为0到9的十个完全相同的球，满足抽奖条件的顾客在袋中摸球，一共摸两次，每次摸出一个球（球放回），如果第一次摸出球的数字比第二次大，则可获奖，则某抽奖顾客获奖概率是（ ）

    A．5%

    B．25%

    C．45%

    D．85%


    正确答案：C
    18．【解析】C。如果摸到0，则中奖概率为90%，如果摸到1，则中奖概率为80%，其余依次为70%，60%，50%，40%，30%，20%，10%，0%，将这10个概率取平均数，则中奖总概率为45%。

  • 第2题：

    一个袋内有l00个球，其中有红球28个、绿球20个、黄球12个、蓝球20个、白球10、黑球10个。现在从袋中任意摸球出来，如果要使摸出的球中，至少有15个球的颜色相同，问至少要摸出几个球才能保证满足上述要求?（ ）

    A．78个

    B．77个 >>>>>

    C．75个

    D．68个


    正确答案：C
    最坏情况：摸出14个红球、14个绿球、12个黄球、14个蓝球、10个白球、10个黑球；则还需要从剩下的球中摸出1个球才能满足要求。即至少要摸出14×3+12+10+10+1=75个球才能满足题目要求。故选C。

  • 第3题：

    一个暗箱装有12个编号从1到12的乒乓球，甲、乙、丙三人轮流从暗箱中摸球，每人每次摸一个球且不放回。将所有球摸完后，三人所摸出的球上的编号之和相等，并且甲摸出了1号球和3号球，乙摸出了6号球和11号球。丙摸出的球编号最大为多少？

    A.7
    B.8
    C.9
    D.10

    答案：C
    解析：
    第一步，本题考查其他杂题。
    第二步，根据题意可知12个球的数字之和为78，由于每个人摸到四个球且编号之和相等，则每人摸到的编号之和为26；甲摸到1号和3号则剩余两个只能为10和12号；乙摸到6号和11号，则剩余的可能为4号，5号或者为2号，7号；那么9号必为丙摸到的。故丙摸出编号最大的为9号。

  • 第4题：

    袋子中有若干黑球和白球。若取出一个黑球，则袋中黑球占总球数的



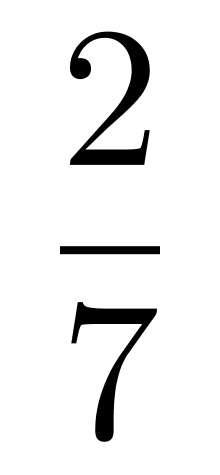
    ；若取出两个白球，则袋中白球占



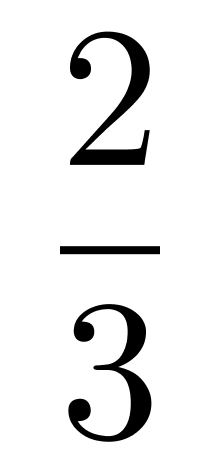
    。从原来袋中抽出3个球，其中有且仅有1个黑球的概率：

    A.低于20%
    B.在20%—40%之间
    C.在40%—60%之间
    D.高于60%

    答案：C
    解析：
    第一步，本题考查概率问题，用方程法解题。

  • 第5题：

    袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以X、Y、Z分别表示两次取球所取得的红、黑与白球的个数。①求②求二维随机变量(X,Y)的概率分布。


    答案：
    解析：

  • 第6题：

    袋中有1个红球、2个黑球与3个白球，现有放回地从袋中取两次，每次取一个球.以X，Y，Z分别表示两次取球所取得的红球、黑球与白球的个数.
    (Ⅰ)求P{X=1｜Z=0}；
    (Ⅱ)求二维随机变量(X，Y)的概率分布.


    答案：
    解析：

  • 第7题：

    有白球和黑球各3个且白球和黑球中各有两个球分别印有1、2两个号码。现将这6个球放入袋子里，充分搅匀后有放回地每次摸取一个球，则前两次恰好摸到同编号的异色球的概率为（ ）。
    A. 4/9 B. 4/15 C. 2/9 D.1/9


    答案：D
    解析：
    D [解析]第一次取到有编号的球的概率为2/3，假设取到白色1号球，则第二次必须取到黑色1号球，其概率为1/6。因此前两次恰好摸到同编号的异色球的概率为2/3 X 1/6 = 1/9。

  • 第8题：

    袋中有l个红球、2个黑球与3个白球，现有放回地从袋中取两次，每次取一个球，以X，y，Z分别表示两次取球所取得的红球、黑球与白球的个数。
    (1)求
    (2)求二维随机变量(X，Y)的概率分布。


    答案：
    解析：

  • 第9题：

    一个袋子里有8个黑球，8个白球，随机不放回地连续取球五次。每次取出1个球，求最多取到3个白球的概率。


    答案：
    解析：

  • 第10题：

    一袋中有2个黑球和若干个白球，现有放回地摸球4次，若至少摸到一个白球的概率是80/81，则袋中白球的个数是（）。


    正确答案:4

  • 第11题：

    单选题
    一个袋内有100个球，其中有红球28个、绿球20个、黄球12个、蓝球20个、白球10个、黑球10个。现在从袋中任意摸球出来，如果要使摸出的球中，至少有15个球的颜色相同，问至少要摸出几个球才能保证满足上述要求？（　　）
    A

    78个

    B

    77个

    C

    75个

    D

    68个


    正确答案： B
    解析：
    设手中有100个球，尽量不发出15个颜色相同的球。先将每种颜色的球发出14个，不足14个的全部发出，则共计发出14＋14＋12＋14＋10＋10＝74个，但剩下的球中任意再发出1个就满足要求了。因此至少要摸出75个球。

  • 第12题：

    单选题
    袋子中装有4个黑球和2个白球，这些球的形状、大小、质地等完全相同，在看不到球的条件下，随机地从袋子中摸出三个球．下列事件是必然事件的是（　　）．
    A

    摸出的三个球中至少有一个球是黑球

    B

    摸出的三个球中至少有一个球是白球

    C

    摸出的三个球中至少有两个球是黑球

    D

    摸出的三个球中至少有两个球是白球


    正确答案： A
    解析：
    因为白球只有2个，所以，摸出三个球中，黑球至少有一个．

  • 第13题：

    袋子里有若干个球，小明每次拿出其中的一半再放回一个球，一共这样做了五次，袋中还有3个球，问原来袋中有多少个球?

    A．18

    B．34

    C．66

    D．158


    正确答案：B
    [答案] B。解析：可以用还原法，第四次操作完是(3-1)×2=4，第三次操作完是(4-1)×2= 6，第二次操作完是(6-1)×2=10，第一次操作完是(10-1)×2=18，原来有(18-1)×2=34。

  • 第14题：

    有白球和黑球各3个且白球和黑球中各有两个球分别印有1、2两个号码。现将这6个球放入袋子里，充分搅匀后有放回地每次摸取一个球，则前两次恰好摸到同编号的异色球的概率为（ ）。


    答案：D
    解析：
    第一次取到有编号的球的概率为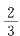，假设取到白色1号球，则第二次必须 取到黑色1号球，其概率为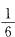。因此前两次恰好摸到同编号的异色球的概率为。。

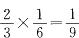  • 第15题：

    袋子中有若干黑球和白球。若取出一个黑球，则袋中黑球占总球数的 2/7；若取出两个白球，则袋中白球占 2/3。从原来袋中抽出3个球，其中有且仅有1个黑球的概率：

    A.低于20%
    B.在20%—40%之间
    C.在40%—60%之间
    D.高于60%

    答案：C
    解析：
    第一步，本题考查概率问题，用方程法解题。

  • 第16题：

    袋子里有若干个球，小明每次拿出其中的一半再放回一个球，一共这样做了五次，袋中还有3个球，问原来袋中有多少个球？( )


    A. 18
    B. 34
    C. 66
    D. 158

    答案：B
    解析：
    解题指导： 反推法，设第五次拿之前剩X：X/2+1=3，则X=4，依次推出剩6、10、18、34，故答案为B。

  • 第17题：

    一个布袋中装有大小相同的3个白球、4个红球和2个黑球，每次从袋中摸出一球不再放回。问恰好在第3次取得黑球的概率是多少？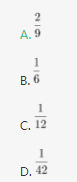


    答案：A
    解析：

  • 第18题：

    一个袋子里面有10个球,包括红球、白球和黑球。已知从袋中任意摸一个球，得到黑球 的概率是2/5，从袋中任意摸两个球,至少有一个是白球的概率是7/9，问袋子里有多少个红球？

    a.l b.2 c.3 d.4


    答案：A
    解析：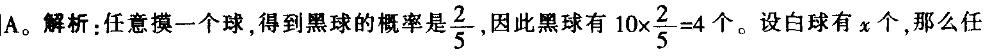

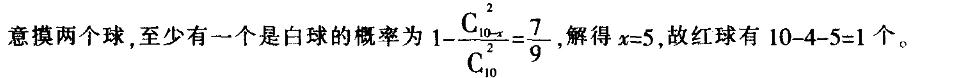
  • 第19题：

    袋子中有70个红球，30个黑球，从袋中任意摸出一个球，观察颜色后放回袋中，再摸第二个球，观察颜色后也放回袋中。

    （1）求两次摸球均为红球的概率；（3分）

    （2）求两次摸球颜色不同的概率。（4分）


    答案：
    解析：
    本题主要考查的是熟练运用分步法、分类法等方法求概率。

    通过不同事件随机发生概率进行分步分类计算。

  • 第20题：

    一个袋子里有8个黑球，8个白球，随机不放回连续取球5次，每次取出1个球，求最多取到3个白球的概率. .?


    答案：
    解析：

  • 第21题：

    袋子中有70个红球，30个黑球，从袋子中连续摸球两次，每次摸一个球，而且是不放回的摸球：

    （1）求两次摸球均为红球的概率。

    （2）若第一次摸到红球，求第二次摸到黑球的概率。


    答案：
    解析：
    本题主要考查求解随机事件的概率方法。

    （1）利用概率近似等于频率，根据相互独立性，可求解两次摸球都是红球的概率。

    （2）由于第一次摸到红球，从剩余的99个球中摸一个黑球，共有30种可能。

  • 第22题：

    设袋中有2个黑球、3个白球，有放回地连续取2次球，每次取一个，则至少取到一个黑球的概率是（）


    正确答案:16/25

  • 第23题：

    问答题
    8.袋中有7个球，其中红球5个白球2个，从袋中取球两次，每次随机地取一个球，取后不放回，求：    (1)第一次取到白球、第二次取到红球的概率；    (2)两次取得一红球一白球的概率．

    正确答案：
    解析： 暂无解析

相关内容