itgle.com

口袋中放有3只红球和11只黄球，这两种球除颜色外没有任何区别，随机从口袋中任取一只球，取到黄球的概率是______．

题目
口袋中放有3只红球和11只黄球，这两种球除颜色外没有任何区别，随机从口袋中任取一只球，取到黄球的概率是______．

相似考题

1.口袋里有大小相同的8个红球和4个黄球，从中任意摸出1个球，摸出红球的可能性是 （ ），摸出黄球的可能性是（ ），摸出（ ）球的可能性最大。

2.口袋里有3个红球和2个白球，球除颜色外完全相同，从中任意摸出1个球。那么，摸出红球的可能性是_____，摸出白球的可能性是_____。要使它们的可能性相同，可以怎么做？

3.圣诞老人的口袋里有相同数量的红，绿两色魔球，魔球除颜色外其他都一样。小朋友可以从里面摸一个魔球作为圣诞礼物，那么淘气摸到绿色魔球的可能性是多少？摸到红色魔球呢？

4.在一个不透明的布袋中装有2个白球和n个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一球，摸到黄球的概率是4/5 ，则n=__________________.

更多“口袋中放有3只红球和11只黄球，这两种球除颜色外没有任何区别，随机从口袋中任取一只球，取到黄球的概率是______．”相关问题

  • 第1题：

    有关C语言的问题

    口袋中有红、黄、蓝、白、黑五种颜色的球若干，每次从口袋中取出3个球。问得到三种不同颜色球的可能选取方法，打印出三种颜色的各种组合。


    循环遍历即可。if (i != j && j !=k && k!=i) -- 三种不同颜色的条件#include <stdio.h>#include <stdlib.h>void main(){int i,j,k,n=0;char c[5][7]={"red","yellow","blue","white","black"};for (i=0;i<5;i++)for (j=i+1;j<5;j++)for (k=j+1;k<5;k++){ if (i != j && j !=k && k!=i) printf("%s %s %s\n",c[i],c[j],c[k]); n++;};printf("n=%d",n);}得：red yellow bluered yellow whitered yellow blackred blue whitered blue blackred white blackyellow blue whiteyellow blue blackyellow white blackblue white blackn=10

  • 第2题：

    （3）一个口袋内装有除颜色外其他都相同的6个白球和4个红球，从中任意摸出2个，求：A、2个都是白球的概率；B、2个都是红球的概率；C、一个白球，一个红球的概率。


    正确答案：
              

  • 第3题：

    一个口袋内有4个不同的红球，6个不同的白球.
    (1)从中任取4个球，红球的个数不比白球少的取法有多少种?
    (2)若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的取法有多少种?


    答案：
    解析：
    解：(1)由题意知本题是一个分类计数问题.将取出4个球分成三类情况：取4个红

  • 第4题：

    袋中有50个乒乓球，其中20个是黄球，30个是白球，今有两人依次随机地从袋中各取一球，取后不放回，则第二个人取得黄球的概率是________.


    答案：
    解析：
    一般理解随机事件“第二个人取得黄球”与第一个人取得的是什么球有关，这就要用全概率公式来计算，但也可以用古典型概率来解，这会简单得多.(方法一)设事件Ai表示第i个人取得黄球，i=1，2，则根据全概率公式：

    (方法二)只考虑第二个人取得的球，这50个球中每一个都会等可能地被第二个人取到，而取到黄球的可能有20个，故所求概率为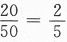

  • 第5题：

    有甲、乙两个口袋,两袋中都有3个白球2个黑球,现从甲袋中任取一球放入乙袋,再从乙袋中任取4个球,设4个球中的黑球数用X表示,求X的分布律.


    答案：
    解析：

  • 第6题：

    一口袋中有3个红球和2个白球，某人从该口袋中随机摸出一球，摸得红球得5分，摸得白球得2分，则他所得分数的数学期望为（ ）

    A.2.5；
    B.3.5；
    C.3.8；
    D.以上都不对

    答案：C
    解析：

  • 第7题：

    一布袋中有红球8个，白球5个和黑球12个，它们除颜色外没有其他区别，随机地从袋中取出1球不是黑球的概率为（ ）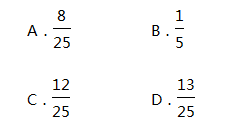


    答案：D
    解析：

  • 第8题：

    一个口袋中有7个红球3个白球，从袋中任取一任球，看过颜色后是白球则放回袋中，直至取到红球，然后再取一球，假设每次取球时各个球被取到的可能性相同，求第一、第二次都取到红球的概率（ ）。

    A.7/10
    B.7/15
    C.7/20
    D.7/30

    答案：B
    解析：
    设A、B分别表示第一、二次红球，则有P（AB）=P（A）P（B|A=7/106/9=7/15。

  • 第9题：

    一口袋有6个白球，4个红球，“无放回”地从袋中取出3个球，则事件“恰有两个红球”的概率为（）


    正确答案:3/10

  • 第10题：

    单选题
    一只盒子中有红球m个，白球10个，黑球n个，每个球除颜色外其他都相同，从中任取一个球，取得白球的概率与不是白球的概率相同，那么m与n的关系是（　　）．
    A

    m＝4，n＝6

    B

    m＝5，n＝5

    C

    m＋n＝5

    D

    m＋n＝10


    正确答案： B
    解析：
    因为从中任取一个球，取得白球的概率与不是白球的概率相同．所以白球的个数与不是白球的球的个数相等，所以m＋n＝10．

  • 第11题：

    问答题
    8.袋中有7个球，其中红球5个白球2个，从袋中取球两次，每次随机地取一个球，取后不放回，求：    (1)第一次取到白球、第二次取到红球的概率；    (2)两次取得一红球一白球的概率．

    正确答案：
    解析： 暂无解析

  • 第12题：

    单选题
    口袋里装有10只外形相同的球，其中7只红球，3只白球．从口袋中任意取出2只球，则它们是一只红球、一只白球的概率等于（）．
    A

    21/90.

    B

    21/45

    C

    21/100

    D

    21/50


    正确答案： C
    解析： 暂无解析

  • 第13题：

    一口袋装有6只球，其中4只白球、2只红球。从袋中取球两次，每次随机地取一只。采用不放回抽样的方式，取到的两只球中至少有一只是白球的概率()

    A、4/9

    B、1/15

    C、14/15

    D、5/9


    参考答案：C

  • 第14题：

    一位乒乓球学员手中拿着装有7只乒乓球的不透明口袋,其中3只黄球，4只白球。他随机取出一只乒乓球，观察颜色后放回袋中，同时放入2只与取出的球同色的球，这样连续取2次，则他取出的两只球中第1次取出的是白球，第2次取出的是黄球的概率是

    A.8/77
    B.4/21
    C.2/11
    D.4/7

    答案：B
    解析：
    第一步，第一次取出白球的概率为4/7。第二步，由题意取出白球后会再放入2个白球，球的总数为9。第二次取出黄球的概率为3/9=1/3，故第一次取出白球，第二次取出黄球的概率为4/7×1/3=4/21。因此，选择B选项。

  • 第15题：

    现有三个箱子,第一个箱子有4个红球,3个白球；第二个箱子有3个红球,3个白球；第三个箱子有3个红球,5个白球；先取一只箱子,再从中取一只球,(1)求取到白球的概率；(2)若取到红球,求红球是从第二个箱子中取出的概率.


    答案：
    解析：

  • 第16题：

    设口袋中有10只红球和15只白球,每次取一个球,取后不放回,则第二次取得红球的概率为_______.


    答案：
    解析：
    设A1={第一次取红球)，A2={第一次取白球），B={第二次取红球），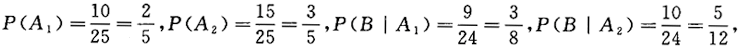　　

    则
    　　

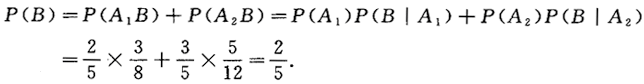
  • 第17题：

    从装有4个红球，4个白球的袋中任取4个球，则所取的4个球中包括两种不同颜色的球的概率是：
    A33/35
    B34/35
    C69/70
    D7/8


    答案：B
    解析：

  • 第18题：

    一个口袋中有4个白球，1个红球，7个黄球．搅匀后随机从袋中摸出1个是白球的概率是_________．


    答案：
    解析：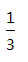

  • 第19题：

    一个口袋中有7个红球3个白球,从袋中任取一球,看过颜色后是白球则放回袋中，直至取到红球,然后再取一球，假设每次取球时各个球被取到的可能性相同，求第一、第二次都取到红球的概率（ ）。

    A.7/10
    B.7/15
    C.7/20
    D.7/30

    答案：B
    解析：
    设AB分别表演一、二次取红球，则有P（AB）=P（A）P（B|A）=7/106/9=7/15。

  • 第20题：

    口袋里装有10只外形相同的球，其中7只红球，3只白球．从口袋中任意取出2只球，则它们是一只红球、一只白球的概率等于（）．

    • A、21/90.
    • B、21/45
    • C、21/100
    • D、21/50

    正确答案:B

  • 第21题：

    袋中有红、黄、蓝球各一个，每一次从袋中任取一球，看过颜色后再放回袋中，共取球三次，颜色全相同的概率为（）

    • A、1／9
    • B、1／3
    • C、5／9
    • D、8／9

    正确答案:A

  • 第22题：

    单选题
    从装有2个红球和2个黑球的口袋内任取2个球，那么互斥而不对立的两个事件是（　　）．
    A

    至少有1个黑球与都是黑球

    B

    至少有1个黑球与至少有1个红球

    C

    恰有1个黑球与恰有2个黑球

    D

    至少有1个黑球与都是红球


    正确答案： C
    解析：
    A项，不互斥也不对立；B项，不互斥也不对立；C项，互斥而不对立；D项，互斥而且对立．

  • 第23题：

    单选题
    袋中有红、黄、蓝球各一个，每一次从袋中任取一球，看过颜色后再放回袋中，共取球三次，颜色全相同的概率为（）
    A

    1／9

    B

    1／3

    C

    5／9

    D

    8／9


    正确答案： D
    解析： 暂无解析

相关内容