itgle.com

对边相等,对角相等的凸四边形,是平行四边形吧?方法①∠B小于90°；左上为A，左下为B，右下为C，右上为D；已知∠B=∠D；AB=CD;证明：过A作AN⊥BC于N； 过C作CM⊥AD于M； 连接AC∵AN⊥BC；CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D；AB=CD∴△ANB=△DMC(AAS）∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°，AC=AC∴△ACD=△AMD（HL）∴AM=DN又∵BN=DM∴BD=AC∵BD=AC；AB=CD∴凸四边形ABCD为平行四边

题目
对边相等,对角相等的凸四边形,是平行四边形吧?

方法①∠B小于90°；

左上为A，左下为B，右下为C，右上为D；

已知∠B=∠D；AB=CD;

证明：过A作AN⊥BC于N；

      过C作CM⊥AD于M；

      连接AC

∵AN⊥BC；CM⊥AD

∴∠ANB=∠DMC=90°

又∵∠B=∠D；AB=CD

∴△ANB=△DMC(AAS）

∴AN=CM;BN=DM

又∵∠ANB=∠DMC=90°，AC=AC

∴△ACD=△AMD（HL）

∴AM=DN

又∵BN=DM

∴BD=AC

∵BD=AC；AB=CD

∴凸四边形ABCD为平行四边型。

方法②∠B大于90°

左上为A，左下为B，右下为C，右上为D；

已知∠B=∠D；AB=CD;

证明：延长CD,过A作AN⊥BC于N；

      延长AB,过C作CM⊥AD于M；

      连接AC

∵AN⊥BC；CM⊥AD

∴∠ANB=∠DMC=90°

又∵∠B=∠D；AB=CD

∴△ANB=△DMC(AAS）

∴AN=CM;BN=DM

又∵∠ANB=∠DMC=90°，AC=AC

∴△ACD=△AMD（HL）

∴AM=DN

又∵BN=DM

∴BD=AC

∵BD=AC；AB=CD

∴凸四边形ABCD为平行四边型。

方法③∠B等于90°

证明：∵∠B=∠D=90°；AB=CD；AC=AC

∴△ABC=△ADC（HL）

∴AB=CB

∵BD=AC；AB=CD

∴凸四边形ABCD为平行四边型。

有错吗？若我的证明有错请明示，我知道有个反例，但它是凹四边形。

相似考题

1.P－304电流运行时显示为()A、50AB、70AC、90AD、20A

2.在平行四边形ABCD中，∠DAB＝60°，AB＝15cm．已知⊙O的半径等于3cm，AB，AD分别与⊙O相切于点E，F，⊙O在平行四边形ABCD内沿AB方向滚动，与BC边相切时运动停止，试求⊙O滚过的路程．

3._______ useful book it is!A.What anB.How aC.What aD.What

4.平行四边形ABCD的周长是28cm，CD－AD＝2cm，则AB的长度是（ ）。A．8cmB．6cmC．7cmD．9cm

参考答案和解析
是平行四边形
更多“对边相等,对角相等的凸四边形,是平行四边形吧? 方法①∠B小于90°；左上为A，左下为B，右下为C，右上为D；已知∠B=∠D；AB=CD;证明：过A作AN⊥BC于N；过C作CM⊥AD于M；连接AC∵AN⊥BC；CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D；AB=CD∴△ANB=△DMC(AAS）∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°，AC=AC∴△ACD=△”相关问题

  • 第1题：

    测深量油尺油高读取顺序为()。

    A.m、dm、cm、mm

    B.m、mm、cm、dm

    C.mm、m、dm、cm

    D.mm、cm、dm、m


    参考答案：D

  • 第2题：

    六边形ABCDEF中，AB∥ED，AF∥CD，BC∥FE，且AB＝ED，AF＝CD，BC＝EF。又FD⊥BD，FD＝24cm，BD＝18cm，则六边形ABCDEF的面积为（）。

    A.432cm2B. 368cm2 C. 216cm2D.以上A、B、C均不正确


    过B点作BG⊥LBD，过F点作FG⊥FD交于G点，连接AG.据已知，则有AGB≌EFD，AGF≌CBD.此时，相当于把EFD平移到AGB，把CBD平移到AGF，则矩形BDFG的面积等于六边形ABCDEF的面积，应为24×l8＝432（cm2）。故正确答案为A.

  • 第3题：

    △ABC中，AB=13cm，BC=10cm，BC边上的中线AD=12cm.求AC  

  • 第4题：

    锐角三角形ABC中，sinA=√5/5，D为BC边上的点，若△ABD 和△ACD的面积分别为2和4，过D作DE ⊥AB于E，DF⊥AC于F，


    答案：
    解析：

  • 第5题：

    如右图，在直角梯形ABCD中，AB,∥CD，AD⊥CD，AB=1cm，AD=6cm，CD=9cm，则BC=________cm．



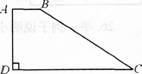    答案：
    解析：

  • 第6题：

    如图，Rt△ABC中，∠ABC=90o,AB=28 cm，以AB为直径的半圆与AC相交，图中的阴影部分①的面积比⑦的面积少28.28 cm2，求BC的长(π取3．14)。


    答案：
    解析：

  • 第7题：

    如图所示，梯形ABCD的两条对角线AD、BC相交于O，EF平行于两条边且过O点。现已知AB=6，CD=18。问EF的长度为多少？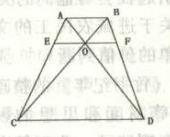


    A. 8.5
    B. 9
    C. 9.5
    D. 10

    答案：B
    解析：
    解题指导： 18*BF/BD=6*DF/BD， BF/DF＝1：3， OF/CD=1:4， OE/CD=1:4， EF=CD/2＝9，故答案为B。

  • 第8题：

    下图为以AC、AD和AF为直径画成的三个圆形，已知AB、BC、CD、DE和EF之间的距离彼此相等。问小圆x、弯月y以及弯月z三部分的面积之比为：

    A.4：5：16
    B.4：5：14
    C.4：7：12
    D.4：3：10

    答案：A
    解析：
    第一步，本题考查几何问题，属于平面几何类。
    第二步，赋值AB＝2，由AB、BC、CD、DE、EF之间的距离相等，可得AC＝4、AD＝6、AF＝10。则小圆、中圆、大圆的半径分别为2、3、5。
    第三步，小圆x、弯月y以及弯月z的面积分别为4π、9π－4π＝5π、25π－9π＝16π，故三部分的面积之比为4∶5∶16。

  • 第9题：

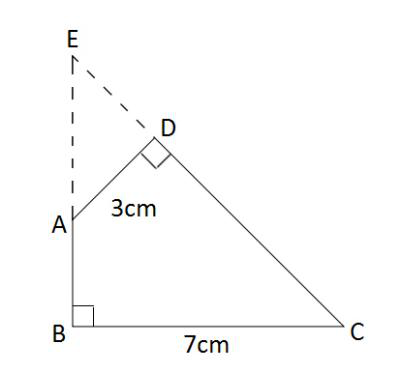
    如图，已知一个四边形中边AD长为3cm，边BC长7cm；∠DAB＝135°，∠ABC=∠ADC=90°那么这个四边形的面积是（ ）。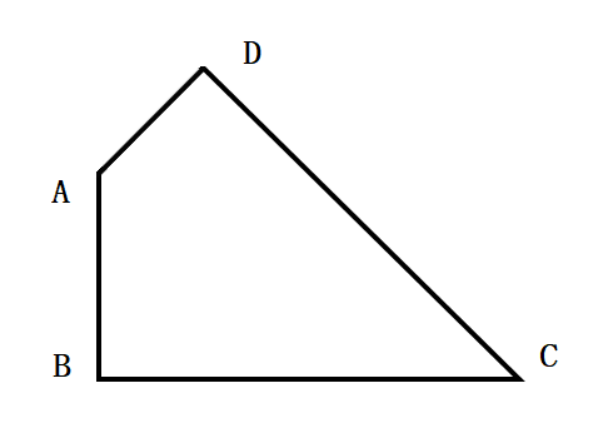


    A.49/4
    B.21
    C.
    D.20


    答案：D
    解析：

  • 第10题：

    测深量油尺油高读取顺序为（）。

    • A、m、dm、cm、mm
    • B、m、mm、cm、dm
    • C、mm、m、dm、cm
    • D、mm、cm、dm、m

    正确答案:D

  • 第11题：

    I earn dollars（）hour as（）supermarket cashier on Saturdays.

    • A、a;an  
    • B、the;a  
    • C、an;a  
    • D、an;the

    正确答案:C

  • 第12题：

    铰链四杆机构ABCD，如果以BC为机架（静件），当机构为双曲柄机构时，各杆的长度可为（）。

    • A、AB=130 BC=150 CD=175 AD=200
    • B、AB=150 BC=130 CD=165 AD=200
    • C、AB=175 BC=130 CD=185 AD=200
    • D、AB=200 BC=150 CD=165 AD=130

    正确答案:C

  • 第13题：

    ______ elephant is much heavier than ______ zebra.

    A、a,an

    B、an,a

    C、the,a

    D、the,an


    参考答案： B

  • 第14题：

    在 △ABC中，∠C=90°，AB=10。（1）∠A=30°，求BC，AC（精确到0.01）；（2）∠A=45°，求BC，AC（精确到0.01）。

  • 第15题：

    试证明如下逻辑函数等式。(1) AB－＋AB－C=AB－;(2) AB(C＋C－)＋AC=AB＋AC;(3) A(BC＋BC)＋AC=A(BC)＋AC


    答案：(1)左边=AB-+AB-C=AB-(1+C)=AB-=右边(2)左边=AB(C+C-)+AC=AB+AC=右边(3)左边=A(BC+BC)+AC=A(BC)+AC=右边

  • 第16题：

    在平行四边形ABCD中，∠DAB=60，AB=15cm，已知圆O的半径等于3cm，AB，AD分别与圆O相切于点E，F.圆0在平行四边形ABCD内沿AB方向滚动，与BC边相切时运动停止．试求圆O滚过的路程．


    答案：
    解析：

  • 第17题：

    如图，在四边形ABCD中，∠ABC=90°，CD⊥AD，AD2+CD2=2AB2.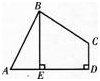

    (1)求证：AB=BC；
    (2)当BE⊥AD于E时，试证明：BE=AE+CD.


    答案：
    解析：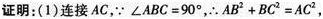



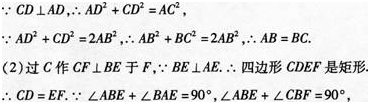
  • 第18题：

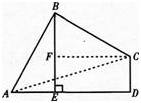
    如图⊙O和⊙O’相交于A，B两点，过A作两圆的切线分别交两圆于C，D两点，连接DB并延长交⊙O于点E.证明：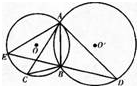

    (1)AC?BD=AD?AB；
    (2)AC=AE.


    答案：
    解析：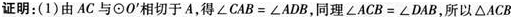


  • 第19题：

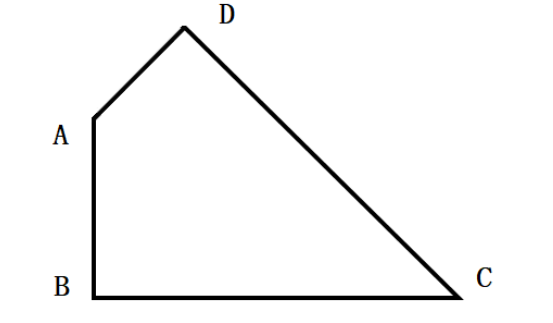
    如图，已知一个四边形中边AD长为3cm，边BC长7cm；∠DAB＝135°，∠ABC=∠ADC=90°那么这个四边形的面积是（ ）cm2。




    答案：D
    解析：
    第一步，本题考查几何问题，用割补平移法解题。
    第二步，作BA和CD的延长线交于E，如图所示，得到三角形EBC和ADE。容易知道所求四边形ABCD面积等于△EBC面积减去△ADE面积。由题意∠DAB＝135°，∠ABC＝∠ADC＝90°，可以求得∠DCB＝360°－135°－90°×2＝45°，且∠BEC＝∠EAD＝45°，所以△EBC和△ADE都是等腰直角三角形。
    第三步，因为AD长3cm，BC长7cm，则BE＝BC＝7cm，DE＝AD＝3cm，所以


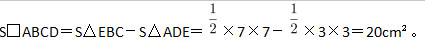
  • 第20题：

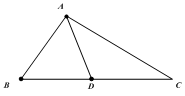
    在三角形ABC，AB=4，AC=6，BC=8，D为BC的中点，则AD=




    答案：B
    解析：

  • 第21题：

    如图1，在△ABC中，BC = 8 cm，AB的垂直平分线交AB于点Ｄ， 交边AC于点E，△BCE的周长等于18 cm，则AC的长等于（ ）

    A、6cm　
    B、8cm
    C、10cm　　
    D、12cm

    答案：C
    解析：

  • 第22题：

    所有对接接头为（）接头。

    • A、AC类
    • B、AD类
    • C、BC类
    • D、AB类

    正确答案:D

  • 第23题：

    已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC，BC为直径作半圆，面积分别记为S1和S2，则S1+S2的值等于4π。


    正确答案:错误

相关内容