itgle.com

多自由度体系的自振频率数n1与主振型数n2的大小关系是： A.n1>n2 B.n12 C.n1=n2 D.不能确定

题目
多自由度体系的自振频率数n1与主振型数n2的大小关系是：

A.n1>n2
B.n12
C.n1=n2
D.不能确定
相似考题

1.主振型的正交性为在多自由度体系中,任意两个不同的主振型之间存在着相互正交的性质。()此题为判断题(对，错)。

2.一个n个自由度的体系,可以有n+1个自振圆频率。()

3.多自由度体系的振型是反应体系自由振动形状的向量。()此题为判断题(对，错)。

4.具有n个自由度的体系,必有()个主振型。A、1B、2C、3D、n

更多“多自由度体系的自振频率数n1与主振型数n2的大小关系是： ”相关问题

  • 第1题：

    多自由度体系的地震反应可通过分解为各阶振型地震反应求解,故称为振型分解法。()

    此题为判断题(对，错)。


    正确答案:正确

  • 第2题：

    图a)体系的自振频率wa与图b)体系的自振频率wb的关系是：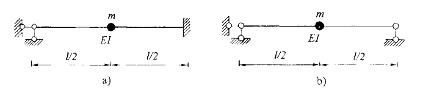


    A. wab
    B. wa>wb
    C.wa=wb
    D.不能确定

    答案：B
    解析：
    提示：w2与k成正比。

  • 第3题：

    振动法（频率法）索力测试，索力是通过下列（ ）等参数计算得到。

    A：索横向自振频率
    B：索的长度
    C：索单位长度的质量
    D：自振频率的阶数
    E：索的横向抗弯刚度

    答案：A,B,C,D,E
    解析：
    需要注意的是，对于粗短索（此时的索不是理想的弦），索的横向抗弯刚度对测试结果存在不可忽视的影响，应进行必要修正，具体修正方法参见相关教材。

  • 第4题：

    图示a、b两体系的EI相同，其自振频率ωa与ωb的关系为（）。

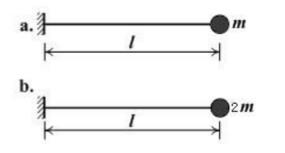
    A不确定

    Bωa＜ωb

    Cωa=ωb

    Dωa＞ωb


    D
    略

  • 第5题：

    关于主振型，下列说法中错误的（）。

    • A、体系有多少个自由度就有多少个主振型
    • B、主振型反映的是结构在振动过程中两质点的位移比值始终保持不变
    • C、主振型不是体系的固有特性，是经常变化的
    • D、主振型具有正交性

    正确答案:C

  • 第6题：

    改变叶片组的叶片数不能改变叶片组的自振频率。


    正确答案:错误

  • 第7题：

    多自由度系统的固有频率和振型（模态）是如何求得的？


    正确答案: 通过求解无阻尼自由振动方程得到

  • 第8题：

    在求解多自由度体系的频率和振型时，既可以计算基本频率也可以计算高阶频率的方法是：（）

    • A、矩阵迭代法
    • B、等效质量法
    • C、能量法
    • D、顶点位移法

    正确答案:A

  • 第9题：

    影响叶片自振频率的因素有哪些？为什么叶片组同一振型的B型振动有若干个自振频率？在大修中实测的叶片自振频率要进行哪些修正才能代表叶片在运行时的自振频率？


    正确答案: 影响动叶片自振频率的因素有：
    （1）动叶片的抗弯刚度，即材料的弹性摸量与叶片截面轴惯性矩的乘积（EI）。抗弯刚度愈大，同一振型的自振频率愈高。
    （2）叶片的长度愈大，叶片同一振型的自振频率愈低。
    （3）叶片同一振型的自振频率与其质量的二次方根成反比。
    （4）动叶片的成组状况，相同的叶片由围带连接成组后，其刚度相应增加，使叶片组的自振频率高于成组前叶片的自振频率。但叶片组产生A型振动时，其围带的质量参于叶片组的振动，使振动部分的质量增加，又使叶片组A型振动的自振频率相应降低。因此叶片组A型振动的自振频率与成组前的叶片相比是提高，还是降低，要具体分析。
    叶片组产生某一B型振动时，由于同一时刻组内各叶片振动的相位可以不同，其围带的变形不同，所产生的反弯矩也不同，使叶片组的抗弯刚度不同，故叶片组同一振型的B型振动有若干各自振频率。
    大修时是在室温条件下测量叶片或叶片组的自振静频率，而运行中叶片在高温条件下高速旋转，因此要对测量的自振静频率进行温度和转速修正，才能代表运行中叶片的自振频率。

  • 第10题：

    判断题
    振动法素力测定试验中，需准确测定索自振频率值，同时还须确定自振频率的阶数。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第11题：

    单选题
    关于主振型，下列说法中错误的（）。
    A

    体系有多少个自由度就有多少个主振型

    B

    主振型反映的是结构在振动过程中两质点的位移比值始终保持不变

    C

    主振型不是体系的固有特性，是经常变化的

    D

    主振型具有正交性


    正确答案： D
    解析： 暂无解析

  • 第12题：

    单选题
    多自由度体系的自振频率数n1与主振型数n2的大小关系是（）
    A

    n1>n2

    B

    n1

    C

    n1=n1

    D

    不能确定


    正确答案： C
    解析： 暂无解析

  • 第13题：

    图示体系的自振频率为（　　）。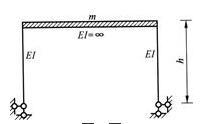



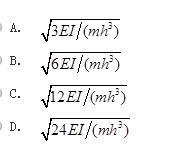    答案：B
    解析：

  • 第14题：

    图a)体系的自振频率wa与图b)体系的自振频率wb的关系是：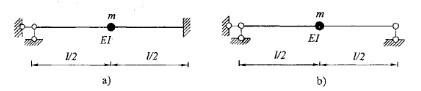

    A. wab B. wa>wb C.wa=wb D.不能确定


    答案：B
    解析：
    提示：w2与k成正比。

  • 第15题：

    振动法索力测定试验中，需准确测定索自振频率值，同时还须确定自振频率的阶数。（ ）


    答案：对
    解析：
    不计索横向刚度时，索力计算公式：T=4WL2fn2/n2式中：T——索张力（N）；W——索线密度（kg/m）；fn——索第n阶横向自振频率（Hz）；L——索计算长度（m）；n——自振频率阶数。索力算式中，索单位长度质量、计算长度可根据设计文件确定，现场需测定的只有自振频率值以及确定自振频率阶数。

  • 第16题：

    图示单自由度动力体系自振周期的关系为（）

    A（a）=（b）

    B（a）=（c）

    C（b）=（c）

    D都不等


    A
    略

  • 第17题：

    多自由度体系的自振频率数n1与主振型数n2的大小关系是（）

    • A、n1>n2
    • B、n1
    • C、n1=n1
    • D、不能确定

    正确答案:C

  • 第18题：

    等直径、等壁厚塔式容器的自振周期是将其简化成（）

    • A、单自由度体系；
    • B、双自由度体系；
    • C、多自由度体系；
    • D、弹性连续体。

    正确答案:D

  • 第19题：

    计算多自由度体系自振频率的方法有（）。

    • A、顶点位移法
    • B、振型分解法
    • C、能量法
    • D、等效质量法
    • E、矩阵迭代法

    正确答案:A,C,D,E

  • 第20题：

    转子的临界转速由（）来决定。

    • A、转子的自振频率
    • B、激振力频率
    • C、自振频率和激振力频率
    • D、自振频率，激振力频率和转子的偏心距

    正确答案:C

  • 第21题：

    单选题
    等直径、等壁厚塔式容器的自振周期是将其简化成（）
    A

    单自由度体系；

    B

    双自由度体系；

    C

    多自由度体系；

    D

    弹性连续体。


    正确答案： A
    解析： 暂无解析

  • 第22题：

    单选题
    对于多自由度振动体系，下列叙述正确的是（）。
    A

    自振频率和振型取决于干扰力的大小和方向

    B

    自振频率和振型取决于初始位移

    C

    自振频率和振型取决于初始速度

    D

    自振频率和振型取决于结构的质量分布和刚度（柔度）系数


    正确答案： B
    解析： 暂无解析

  • 第23题：

    问答题
    影响叶片自振频率的因素有哪些？为什么叶片组同一振型的B型振动有若干个自振频率？在大修中实测的叶片自振频率要进行哪些修正才能代表叶片在运行时的自振频率？

    正确答案： 影响动叶片自振频率的因素有：
    （1）动叶片的抗弯刚度，即材料的弹性摸量与叶片截面轴惯性矩的乘积（EI）。抗弯刚度愈大，同一振型的自振频率愈高。
    （2）叶片的长度愈大，叶片同一振型的自振频率愈低。
    （3）叶片同一振型的自振频率与其质量的二次方根成反比。
    （4）动叶片的成组状况，相同的叶片由围带连接成组后，其刚度相应增加，使叶片组的自振频率高于成组前叶片的自振频率。但叶片组产生A型振动时，其围带的质量参于叶片组的振动，使振动部分的质量增加，又使叶片组A型振动的自振频率相应降低。因此叶片组A型振动的自振频率与成组前的叶片相比是提高，还是降低，要具体分析。
    叶片组产生某一B型振动时，由于同一时刻组内各叶片振动的相位可以不同，其围带的变形不同，所产生的反弯矩也不同，使叶片组的抗弯刚度不同，故叶片组同一振型的B型振动有若干各自振频率。
    大修时是在室温条件下测量叶片或叶片组的自振静频率，而运行中叶片在高温条件下高速旋转，因此要对测量的自振静频率进行温度和转速修正，才能代表运行中叶片的自振频率。
    解析： 暂无解析

  • 第24题：

    多选题
    计算多自由度体系自振频率的方法有（）。
    A

    顶点位移法

    B

    振型分解法

    C

    能量法

    D

    等效质量法

    E

    矩阵迭代法


    正确答案： D,B
    解析： 暂无解析

相关内容