如果X的取值无法一一列出,可以遍取某个区间的任意数值,则称为( )。 A、离散型随机变量 B、分布型随机变量 C、连续型随机变量 D、中断型随机变量
题目
B、分布型随机变量
C、连续型随机变量
D、中断型随机变量
相似考题
更多“如果X的取值无法一一列出,可以遍取某个区间的任意数值,则称为( )。 ”相关问题
-
第1题:
认识一个随机变量X的关键就是要知道它的分布,分布包含的内容有( )。
A.X可能取哪些值
B.X在哪个区间上取值
C.X取这些值的概率各是多少
D.X在任一区间上取值的概率是多少
E.随机变量在固定区间的取值频率是多少
正确答案:ABCD
解析:随机变量的取值是随机的,但内在还是有规律性的,这个规律性可以用分布来描述。认识一个随机变量X的关键就是要知道它的分布,分布包含两方面内容:①X可能取哪些值,或在哪个区间上取值;②X取这些值的概率各是多少,或X在任一区间上取值的概率是多少。 -
第2题:
离散变量可以( )。
A.被无限分割,无法一一列举 B.按一定次序一一列举,通常取整数
C.连续取值,取非整数 D.用间断取值,无法一一列举
正确答案:B
-
第3题:
如果对于给定的一组数值,所构造出的--X树的带权路径长度最小,则该树称为【 】。
正确答案:哈夫曼树(或最优二叉树)
哈夫曼树(或最优二叉树) 解析:扩充二叉树概念:当二叉树里出现空的子树时,就增加新的特殊的结点——外部结点。对于原来的二叉树中度为1的分支结点,在它下面增加一个外部结点;对于原来二叉树的树叶,在它下面增加两个外部结点。哈夫曼树构成:利用哈夫曼算法构造的具有最小带权外部路径长度的扩充二叉树,即所构造的二叉树对于给定的权值,带权路径长度最小。由哈夫曼树的构成我们得知,题意所给条件完全符合哈夫曼树。 -
第4题:
已知(x)在区间(-∞,+∞)内为单调减函数,且(x)>(1),则x的取值范围是().A.(-∞,-l)
B.(-∞,1)
C.(1,+∞)
D.(-∞,+∞)答案:B解析:利用单调减函数的定义可知:当(x)>(1)时,必有x<1. -
第5题:
(2016年)如果X的取值无法一一列出,可以遍取某个区间的任意数值,则称为()。A.离散型随机变量
B.分布型随机变量
C.连续型随机变量
D.中断型随机变量答案:C解析:如果一个随机变量X最多只能取可数的不同值,则为离散型随机变量;如果x的取值无法一一列出,可以遍取某个区间的任意数值,则为连续型随机变量。 -
第6题:
下列关于随机变量的说法中,正确的有( )。
Ⅰ.如果一个随机变量X最多只能取可数的不同值,则为离散型随机变量
Ⅱ.如果X的取值无法一一列出,可以遍取某个区间的任意数值,则为连续型随机变量
Ⅲ.A公司发行的普通股股价在未来某一天的收盘价S可以是5元,可以是10元,也可以是5~10元的任意一个数值,于是S是一个随机变量
Ⅳ.我们将一个能取得多个可能值的数值变量X称为随机变量A:Ⅰ.Ⅱ.Ⅲ.Ⅳ
B:Ⅰ.Ⅱ.Ⅲ
C:Ⅰ.Ⅱ.Ⅳ
D:Ⅲ.Ⅳ答案:A解析:题中四个选项均是对随机变量的正确描述。 -
第7题:
函数y=x2-2ax+1,若它的增区间是[2,+∞),则a的取值是多少?若它在区间[2,+∞)上递增,则a的取值范围是什么?
正确答案: a=2;a≤2。 -
第8题:
如果一个随机变量允许在某个给定的范围内任意取值,则它就是一个()
- A、随机数
- B、随机数分布
- C、离散的随机变量
- D、连续的随机变量
正确答案:D -
第9题:
所有取值能一一列出的随机变量称为()
正确答案:离散型随机变量 -
第10题:
单选题任意一个由二进制位串组成的代码都可以和一个系数仅为‘0’和‘1’取值的多项式一一对应。则二进制代码10111对应的多项式为()。Ax4+x2+x+1
Bx6+x4+x2+x+1
Cx5+x3+x2+x+1
Dx5+x3+x+1
正确答案: C解析: 暂无解析 -
第11题:
多选题一对互为对偶的问题存在最优解,则在其最优点处有()A若某个变量取值为0,则对应的对偶约束为严格的不等式
B若某个变量取值为正,则相应的对偶约束必为等式
C若某个约束为等式,则相应的对偶变取值为正
D若某个约束为严格的不等式,则相应的对偶变量取值为0
E若某个约束为等式,则相应的对偶变量取值为0
正确答案: D,C解析: 暂无解析 -
第12题:
单选题计量值数据是可以连续取值的数据,属于连续型变量,其特点是()A在任意两个数值之间都可以取精度较高一级的数值
B在任意两个数值之问只能取精度较低一级的数值
C只能损顺序数列取值
D表示具有某一质量标准的产品数量
正确答案: B解析: 暂无解析 -
第13题:
连续型随机变量,其取值为________。
A.仅取数轴上有限个点
B.取数轴上无限可列个点
C.取数轴上的任意点
D.取数轴上某一区间上所有的点
正确答案:D
解析:若一个随机变量的所有可能取值充满数轴上某一区间(a,b),则称此随机变量为连续型随机变量。 -
第14题:
下列关于随机变量的说法,错误的是()。
A.我们将一个能取得多个可能值的数值变量X称为随机变量
B.如果一个随机变量X最多只能取可数的不同值,则为离散型随机变量
C.如果X的取值无法一一列出,可以遍取某个区间的任意数值,则为连续型随机变量
D.我们将一个能取得多个可能值的数值变量X称为分散变量
正确答案:D
我们将一个能取得多个可能值的数值变量X称为随机变量。 -
第15题:
已知-1已知-1<x+y<4且2<x-y<3,则z=2x-3y的取值范围是 .(答案用区间表示)
正确答案:
(3,8)第16题:
下列关于随机变量的说法,错误的是( )。A、我们将一个能取得多个可能值的数值变量X称为随机变量
B、如果一个随机变量X最多只能取可数的不同值,则为离散型随机变量
C、如果X的取值无法一一列出,可以遍取某个区间的任意数值,则为连续型随机变量
D、我们将一个能取得多个可能值的数值变量X称为分散变量答案:D解析:我们将一个能取得多个可能值的数值变量X称为随机变量。第17题:
下列关于随机变量的说法中,正确的有( )。
Ⅰ.如果一个随机变量X最多只能取可数的不同值,则为离散型随机变量
Ⅱ.如果X的取值无法一一列出,可以遍取某个区间的任意数值,则为连续型随机变量
Ⅲ.A公司发行的普通股股价在未来某一天的收盘价S可以是5元,可以是10元,也可以是5~10元的任意一个数值,于是S是一个随机变量
Ⅳ.我们将一个能取得多个可能值的数值变量X称为随机变量A.Ⅰ.Ⅱ.Ⅲ.Ⅳ
B.Ⅰ.Ⅱ.Ⅲ
C.Ⅰ.Ⅱ.Ⅳ
D.Ⅲ.Ⅳ答案:A解析:题中四个选项均是对随机变量的正确描述。第18题:
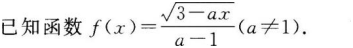
(1)若a>0,则?(x)的定义域是__________;
(2)若?(x)在区间(0,1]上是减函数,则实数a的取值范围是__________.答案:解析: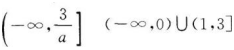
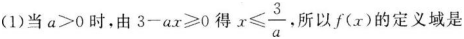

第19题:
一对互为对偶的问题存在最优解,则在其最优点处有()
- A、若某个变量取值为0,则对应的对偶约束为严格的不等式
- B、若某个变量取值为正,则相应的对偶约束必为等式
- C、若某个约束为等式,则相应的对偶变取值为正
- D、若某个约束为严格的不等式,则相应的对偶变量取值为0
- E、若某个约束为等式,则相应的对偶变量取值为0
正确答案:B,D第20题:
某个体的适应度函数值越大,则该个体的性能()
- A、越好
- B、越坏
- C、不变
- D、无法确定
正确答案:A第21题:
在逻辑运算中,能把所有可能条件组合及其结果一一对应列出的表格称为数值表。
正确答案:错误第22题:
填空题所有取值能一一列出的随机变量称为()正确答案: 离散型随机变量解析: 暂无解析第23题:
问答题函数y=x2-2ax+1,若它的增区间是[2,+∞),则a的取值是多少?若它在区间[2,+∞)上递增,则a的取值范围是什么?正确答案: a=2;a≤2。解析: 函数y=x2-2ax+1图象的对称轴为直线x=a,递增区间为[a,+∞)。若它的增区间是[2,+∞),则a=2;若它在区间[2,+∞)上递增,则区间[2,+∞)是区间为[a,+∞)子区间,从而a的取值范围是a≤2。
