itgle.com

已知效用函数为U=㏒aX+㏒aY，预算约束为：PXX+PYY=M。求：①消费者均衡条件②X与Y的需求函数③X与Y的需求的点价格弹性

题目

已知效用函数为U=㏒aX+㏒aY，预算约束为：PXX+PYY=M。求：①消费者均衡条件②X与Y的需求函数③X与Y的需求的点价格弹性

相似考题

1.某消费者消费X和Y两种商品所获得的效用函数为：U=XY+Y，预算约束为：PX X + PYY = I，求： 说明X和Y之间是替代品、互补品还是独立商品

2.某消费者对商品x和商品y的效用函数为u（x，y）=x-0.5x2+y。商品x的价格为p，商品y的价格标准化为1。问题：写出该消费者对商品x的需求函数。

3. 某消费者消费X和Y两种商品所获得的效用函数为：U=XY+Y，预算约束为：PX X + PYY = I，求： X、Y的需求函数

4.某人的效用函数为收入为m，其中x和y的价格分别为p1，p2。 求出消费者均衡时，该人对x，y两商品的需求函数。

更多“已知效用函数为U=㏒aX＋㏒aY，预算约束为：PXX＋PYY=M。求：①消费者均衡条件②X与Y的需求函数③X与Y的需求 ”相关问题

  • 第1题：

    某消费者消费X和Y两种商品所获得的效用函数为：U=XY+Y，预算约束为：PX X + PYY = I，求： （1）若PX =2元，PY=1元，I=10元，求最大的总效用及收入边际效用

    （2）若PY上升到了4元，为保持问题（1）中的总效用不变，消费者需要花多少钱？


    答案：
    解析：
    若PX =2元，PY=1元，I=10元则购买的两种商品量为X=2，Y=6 则总效用U=2·6+6=18

    若PY上升到了4元，如果此时的收入变为I*，则购买两种商品量为：


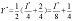
    如果保持消费者在（3）问中的总效用不变的则XY+Y=18，把求出的两种商品的购买量代入，求出此时的收入水平为：I*=22，即消费者此时需要花费22元才能维持效用水平不变。

  • 第2题：

    I = Px·X + Py·Y 是消费者的

    A．需求函数

    B．效用函数

    C．预算约束方程

    D．不确定


    q=1/(36乘p的2次方)；q=1/（36乘p的2次方）p=1/(6乘q的1/2次方)；p=1/（6乘q的1/2次方）1/3

  • 第3题：

    I = Px · X + Py•Y 是消费者的

    A．需求函数

    B．效用函数

    C．预算约束方程

    D．不确定


    q=1/(36乘p的2次方)；q=1/（36乘p的2次方）p=1/(6乘q的1/2次方)；p=1/（6乘q的1/2次方）1/3

  • 第4题：

    设某消费者的效用函数为柯布-道格拉斯类型的，即U=x^αy^β,商品x和商品y的价格分别为Px和Py，消费者收入为M，α和β为常数切α+β=1 (1)求该消费者关于商品x和商品y的需求函数。 (2)证明：当商品x和y的价格及消费者的收入均以相同的比例变化时，消费者对两商品的需求关系维持不变； (3)证明：该消费者效用函数中的参数α和β分别为商品x和商品y的消费支出占消费者收入的份额。


    答案：
    解析：

    综上，消费者效用函数中的参数α和β分别为商品x和商品y的消费支出占消费者收入的份额。

  • 第5题：

    在分析消费者行为理论中，I=PxX+PyY（其中I：收入；Px：商品X价格；Py：商品Y的价格）是消费者的（）。

    A．需求函数

    B．效用函数

    C．预算约束函数

    D．不确定函数


    预算约束函数

相关内容