itgle.com
若x*是f（x)=0的重根，则牛顿不收敛。
题目
若x*是f（x)=0的重根，则牛顿不收敛。
相似考题
参考答案和解析
更多“若x*是f（x)=0的重根，则牛顿不收敛。”相关问题
-
第1题：
解非线性方程f(x)=0的牛顿迭代法在重根附近()A、线性收敛
B、三次收敛
C、平方收敛
D、不收敛
参考答案：A
-
第2题：
设求方程f(x)=0的根的牛顿法收敛，则它具有()敛速。
A、超线性
B、平方
C、线性
D、三次
参考答案：C
-
第3题：
下列命题中，哪个是正确的？A.周期函数f（x）的傅立叶级数收敛于f（x）
B.若f（x）有任意阶导数，则f（x）的泰勒级数收敛于f（x）
C.若正项级数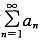
收敛，则
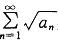必收敛
D.正项级数收敛的充分且必-条件是级数的部分和数列有界答案：D解析：提示：本题先从熟悉的结论着手考虑，逐一分析每一个结论。选项D是正项级数的基本定理，因而正确，其余选项均错误。选项A，只在函数的连续点处级数收敛于f（x）；选项B，级数收敛，还需判定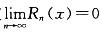
；选项C，可通过举反例说明，级数
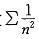收敛，但
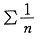发散。 -
第4题：
若f（-x）=f（x），且在（0，+∞）内f′（x）＞0，f″（x）＜0，则f（x）在（-∞，0）内（ ）。A.f′（x）＜0，f″（x）＜0
B.f′（x）＜0，f″（x）＞0
C.f′（x）＞0，f″（x）＜0
D.f′（x）＞0，f″（x）＞0答案：A解析：已知在给出的（0，+∞）内，f′（x）＞0，f″（x）＜0，故在（0，+∞）上f（x）单调递增，且图形是凸的，再根据已知条件f（-x）=f（x）可知f（x）是偶函数，利用图形的对称性可得出f（x）在（-∞，0）是单调递减且也是凸的。故应该选择A。 -
第5题：
下列命题正确的是（）A.函数f(x)的导数不存在的点，一定不是f(x)的极值点
B.若x0为函数f(x)的驻点，则x0必为f(x)的极值点
C.若函数f(x)在点x0处有极值，且f'(x0)存在，则必有f'(x0)＝0
D.若函数f(x)在点x0处连续，则f'(x0)一定存在答案：C解析：根据函数在点x0处取极值的必要条件的定理，可知选项C是正确的． -
第6题：
下列命题中正确的为（）A.若xo为f(x)的极值点，则必有，f'(xo)=0
B.若f'(xo)=0，则点xo必为f(x)的极值点
C.若f'(xo)≠0，则点xo必定不为f(x)的极值点
D.若f(x)在点xo处可导，且点xo为f(x)的极值点，则必有f'(xo)=0答案：D解析：由极值的必要条件知D正确．Y=|x|在x=0处取得极值，但不可导，知A与C不正确．y=x3在xo=0处导数为0，但Xo=0不为它的极值点，可知B不正确．因此选D． -
第7题：
若f（x）∈F[x]，若c∈F使得f（c）=0，则称c是f（x）在F中的一个根。
正确答案:正确 -
第8题：
若a，b是方程f（x）=0的两个相异的实根，f（x）在［a，b］上连续，且在（a，b）内可导，则方程f’（x）=0在（a，b）内（）．
- A、只有一个根
- B、至少有一个根
- C、没有根
- D、以上结论都不对
正确答案:B -
第9题：
判断题若f（x）∈F[x]，若c∈F使得f（c）=0，则称c是f（x）在F中的一个根。A对
B错
正确答案： 对解析： 暂无解析 -
第10题：
单选题设f（x，y）与φ（x，y）均为可微函数，且φy′（x，y）≠0。已知（x0，y0）是f（x，y）在约束条件φ（x，y）＝0下的一个极值点，下列选项正确的是（ ）。A若fx′（x0，y0）＝0，则fy′（x0，y0）＝0
B若fx′（x0，y0）＝0，则fy′（x0，y0）≠0
C若fx′（x0，y0）≠0，则fy′（x0，y0）＝0
D若fx′（x0，y0）≠0，则fy′（x0，y0）≠0
正确答案： A解析：
设z＝f（x，y）＝f（x，y（x）），由题意可知∂z/∂x＝fx′＋fy′·（dy/dx）＝0。
又φ（x，y）＝0，则dy/dx＝－φx′/φy′。故fx′－（φx′/φy′）fy′＝0。又φy′≠0，则fx′φy′＝φx′fy′。所以当fx′≠0时fy′≠0。 -
第11题：
单选题若f（－x）＝－f（x）（－∞＜x＜＋∞），且在（－∞，0）内f′（x）＞0，f″（x）＜0，则f（x）在（0，＋∞）内是（ ）。[2013年真题]Af′（x）＞0，f″（x）＜0
Bf′（x）＜0，f″（x）＞0
Cf′（x）＞0，f″（x）＞0
Df′（x）＜0，f″（x）＜0
正确答案： C解析：
由f（－x）＝－f（x）（－∞＜x＜＋∞），知f（x）为奇函数，奇函数关于原点对称。根据奇函数图形，故在（0，＋∞）内，f′（x）＞0，f″（x）＞0。 -
第12题：
单选题（2013）若f（-x）=-f（x）（-∞0，f″（x）<0，则f（x）在（0，+∞）内是：（）Af′（x）>0，f″（x）<0
Bf′（x）<0，f″（x）>0
Cf′（x）>0，f″（x）>0
Df′（x）<0，f″（x）<0
正确答案： C解析： 暂无解析 -
第13题：
设求方程f(x)=0的根的牛顿法收敛,则它具有()收敛。A、超线性
B、平方
C、线性
D、三次
参考答案：C
-
第14题：
设f（x）在（-∞，+∞）上是偶函数，若f'（-x0）=-K≠0，则f(x0)等于:
答案：B解析：提示：利用结论“偶函数的导函数为奇函数”计算。
f（-x）=f（x），求导-f'（-x）=f'（x），即f'（-x）=-f'（x）。将x=x0代入，得f'（-x0）=-f'（x0），解出f'（x0）=K。 -
第15题：
下列命题正确的是().
A若|f(x)|在x=a处连续,则f(x)在x=a处连续
B若f(x)在x=a处连续,则|f(x)|在x=a处连续
C若f(x)在x=a处连续,则f(x)在z-a的一个邻域内连续
D若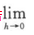
［f(a+h)－f(a-h)］=0,则f(x)在x=a处连续答案：B解析：
-
第16题：
下列命题中，哪个是正确的？
A.周期函数f(x)的傅立叶级数收敛于f (x)
B.若f(x)有任意阶导数，则f(x)的泰勒级数收敛于f(x)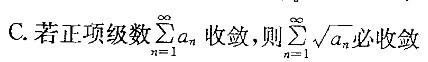
D.正项级数收敛的充分且“条件是级数的部分和数列有界答案：D解析：提示:本题先从熟悉的结论着手考虑，逐一分析每一个结论。选项D是正项级数的基本定理，因而正确，其余选项均错误。选项A，只在函数的连续点处级数收敛于f(x)；选项B，级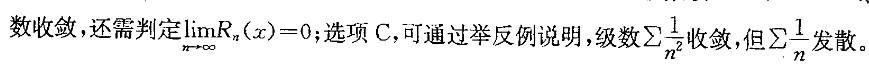
-
第17题：
若函数f(x)满足方程f"(x)+f'(x)-2f(x)=0及f"(x)+f(x)=2e……x，则f(x)=________.答案：1、e^x.解析：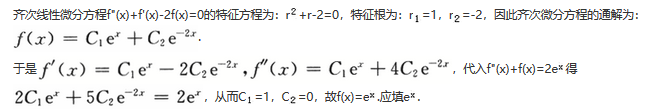
-
第18题：
用牛顿切线法解方程f（x）=0，选初始值x0满足（），则它的解数列{xn}n=0，1，2，…一定收敛到方程f（x）=0的根。
- A、f（x0）f″（x）>0
- B、f（x0）f′（x）>0
- C、f（x0）f″（x）<0
- D、f（x0）f′（x）<0
正确答案:A -
第19题：
解非线性方程f（x）=0的牛顿迭代法具有（）收敛。
正确答案:局部平方 -
第20题：
单选题用牛顿切线法解方程f（x）=0，选初始值x0满足（），则它的解数列{xn}n=0，1，2，…一定收敛到方程f（x）=0的根。Af（x0）f″（x）>0
Bf（x0）f′（x）>0
Cf（x0）f″（x）<0
Df（x0）f′（x）<0
正确答案： A解析： 暂无解析 -
第21题：
填空题解非线性方程f（x）=0的牛顿迭代法具有（）收敛。正确答案： 局部平方解析： 暂无解析 -
第22题：
单选题下列说法中正确的是（ ）。[2014年真题]A若f′（x0）=0，则f（x0）必须是f（x）的极值
B若f（x0）是f（x）的极值，则f（x）在点x0处可导，且f′（x0）=0
C若f（x0）在点x0处可导，则f′（x0）=0是f（x）在x0取得极值的必要条件
D若f（x0）在点x0处可导，则f′（x0）=0是f（x）在x0取得极值的充分条件
正确答案： B解析：
当f（x0）在点x0处可导时，若f（x）在x0处取得极值，则可知f′（x0）=0；若f′（x0）＝0，f（x）在点x0未必取得极值，例如f（x）＝x3在点x＝0处有f′（0）＝0，但x3在实数域内不存在极值点。 -
第23题：
单选题设函数f（x）在（－∞，＋∞）内单调有界，{xn}为数列，下列命题正确的是（ ）。A若{xn}收敛，则{f（xn）}收敛
B若{xn}单调，则{f（xn）}收敛
C若{f（xn）}收敛，则{xn}收敛
D若{f（xn）}单调，则{xn}收敛
正确答案： A解析：
由题意知，若{xn}单调，则{f（xn）}单调有界，则{f（xn）}一定存在极限，即{f（xn）}收敛。 -
第24题：
单选题设求方程f（x）=0的根的牛顿法收敛，则它具有（）敛速。A超线性
B平方
C线性
D三次
正确答案： D解析： 暂无解析