itgle.com

如果f(x)对任何x都满足f(1＋x)=2f(x),且f(0)存在,f’(0)=2,则f’(1)=()。A．4B．-4C．8D．-8

题目
如果f(x)对任何x都满足f(1＋x)=2f(x),且f(0)存在,f’(0)=2,则f’(1)=()。

A．4

B．-4

C．8

D．-8

相似考题

1.曲线y=f(x)在点(x0,f(x0))有拐点,且f''(x0)存在,则f''(x0)=1。()此题为判断题(对，错)。

2.设f(x)连续且F(x)=f(x)dt,则F(x)为().A.2a B.a2f(a) C.0 D.不存在

3.设随机变量X的密度函数为f(x)，且f(-x)=f(x)，F(x)是X的分布函数，则对任意实数a有( )。A. B. C.F(-a)=F(a) D.F(-a)=2F(a)-1

4.A.f′（x） B.f′（0） C.f（0） D.1/2f（0）

参考答案和解析

参考答案：A
参考解析： 只能用函数在一点的导数定义求之．因为只知道f’(0)，不知道f(x)在其他点处是否可导，所以不能在所给等式两端对x求导，再求出f’(1)．
由条件f(1+x)=2f(x)知
f(1)=f(1+0)=2f(0)．
根据导数定义得

更多“如果f(x)对任何x都满足f(1＋x)=2f(x),且f(0)存在,f’(0)=2,则f’(1)=()。 ”相关问题

  • 第1题：

    若f（-x）=f（x），且在（0，+∞）内f′（x）＞0，f″（x）＜0，则f（x）在（-∞，0）内（ ）。

    A.f′（x）＜0，f″（x）＜0
    B.f′（x）＜0，f″（x）＞0
    C.f′（x）＞0，f″（x）＜0
    D.f′（x）＞0，f″（x）＞0

    答案：A
    解析：
    已知在给出的（0，+∞）内，f′（x）＞0，f″（x）＜0，故在（0，+∞）上f（x）单调递增，且图形是凸的，再根据已知条件f（-x）=f（x）可知f（x）是偶函数，利用图形的对称性可得出f（x）在（-∞，0）是单调递减且也是凸的。故应该选择A。

  • 第2题：

    已知函数f(x）=f(x+4),f(0）=0，且在（—2，2）上有f'(x)=|x|,则f(19)=



    答案：C
    解析：
    由f(x）=f(x+4),知f(x)是周期为4的周期函数，故f(19)=f(-1），

  • 第3题：

    43、若随机变量X~N（0, 1), 其分布函数和概率密度函数分别为F（x)和f（x), 则对任意实数a有：

    A．F(a)=1-F(-a)

    B．f(-a)=f(a)

    C．P(X|≤a)=2F(a)-1

    D．F(0)=0.5


    7+24+38+24+7=100则 查表可得φ(1．5)≈0．93φ(0．5)≈0．69．由题设得 令x= （y-60)=1．5解得y=64．5即x 4 =64．5由对称性得x 1 =60-(64．5-60)=55．5再令 (y-60)=0．5解得y=61．5即x 3 =61．5由对称性得 x 2 =60-(61．5-60)=58．5 7+24+38+24+7=100,则 查表可得φ(1．5)≈0．93,φ(0．5)≈0．69．由题设得 令x= （y-60)=1．5,解得y=64．5,即x4=64．5,由对称性得x1=60-(64．5-60)=55．5,再令 (y-60)=0．5,解得y=61．5,即x3=61．5,由对称性得x2=60-(61．5-60)=58．5

  • 第4题：

    若函数f(x)满足方程f"(x)+f'(x)-2f(x)=0及f"(x)+f(x)=2e……x，则f(x)=________.


    答案：1、e^x.
    解析：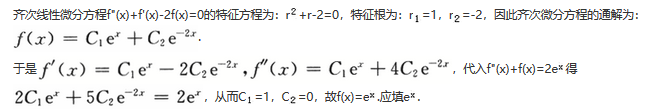

  • 第5题：

    若f（-x）=f（x），且在（0，+∞）内f′（x）＞0，f″（x）＜0，则f（x）在（-∞，0）内（ ）。《》（ ）

    A.f′（x）＜0，f″（x）＜0
    B.f′（x）＜0，f″（x）＞0
    C.f′（x）＞0，f″（x）＜0
    D.f′（x）＞0，f″（x）＞0

    答案：A
    解析：
    已知在给出的（0，+∞）内，f′（x）＞0，f″（x）＜0，故在（0，+∞）上f（x）单调递增，且图形是凸的，再根据已知条件f（-x）=f（x）可知f（x）是偶函数，利用图形的对称性可得出f（x）在（-∞，0）是单调递减且也是凸的。故应该选择A。

相关内容