itgle.com

（ 53 ）设 U 为所有属性， X 、 Y 、 Z 为属性集， Z = U - X - Y 。 下面关于平凡的多值依赖的叙述中，哪一条是正确的？A ）若 X →→ Y ， 且 Z ＝ Ф ，则称 X →→ Y 为平凡的多值依赖B ）若 X →→ Y ， 且 Z ≠Ф ，则称 X →→ Y 为平凡的多值依赖C ）若 X → Y ， 且 X →→ Y ， 则称 X →→ Y 为平凡的多值依赖D ）若 X →→ Y ， 且 X →→ Z ， 则称 X →→ Y 为平凡的多值依赖

题目

（ 53 ）设 U 为所有属性， X 、 Y 、 Z 为属性集， Z = U - X - Y 。 下面关于平凡的多值依赖的叙述中，哪一条是正确的？

A ）若 X →→ Y ， 且 Z ＝ Ф ，则称 X →→ Y 为平凡的多值依赖

B ）若 X →→ Y ， 且 Z ≠Ф ，则称 X →→ Y 为平凡的多值依赖

C ）若 X → Y ， 且 X →→ Y ， 则称 X →→ Y 为平凡的多值依赖

D ）若 X →→ Y ， 且 X →→ Z ， 则称 X →→ Y 为平凡的多值依赖

相似考题

1.设U为所有属性,X、Y、Z为属性集，Z=U-X-Y，下列关于平凡的多值依赖的叙述中，哪一条是正确的？A．若X→→Y，Z=?，则称X→→Y为平凡的多值依赖B．若X→→Y，Z≠?，则称X→→Y为平凡的多值依赖C．若X→Y，X→→Y，则称X→→Y为平凡的多值依赖D．若X→→Y，X→→Z，则称X→→Y为平凡的多值依赖

2.设U为所有属性,X、Y、Z为属性集，Z=U-X-Y，下列关于平凡的多值依赖的叙述中，哪一条是正确的？A．若X→→Y，Z=Φ，则称X→→Y为平凡的多值依赖B．若X→→Y，Z≠Φ，则称X→→Y为平凡的多值依赖C．若X→Y，X→→Y，则称X→→Y为平凡的多值依赖D．若X→→Y，X→→Z，则称X→→Y为平凡的多值依赖

3.设U为所有属性，X、Y、Z为属性集，Z=U-X-Y。下面关于平凡的多值依赖的叙述中，哪一条是正确的?A．若X→→Y，且Z=，则称X→→Y为平凡的多值依赖B．若X→→Y，且Z≠，则称X→→Y为平凡的多值依赖C．若X→Y，且X→→Y，则称X→→Y为平凡的多值依赖D．若X→→Y，且X→→Z，则称X→→Y为平凡的多值依赖

4.（53）设 U 为所有属性，X、Y、Z 为属性集，Z = U Y，下列关于平凡的多值依赖的叙述中，哪一条是正确的？A）若 X→→Y，Z=? ，则称 X→→Y 为平凡的多值依赖B）若 X→→Y，Z?? ，则称 X→→Y 为平凡的多值依赖C）若 X→Y，X→→Y ，则称 X→→Y 为平凡的多值依赖D）若 X→→Y，X→→Z，则称 X→→Y 为平凡的多值依赖

更多“( 53 )设 U 为所有属性, X 、 Y 、 Z 为属性集, Z = U － X － Y 。 下面关于平凡的多值依赖的叙述中, ”相关问题

  • 第1题：

    设U为所有属性，X、Y、Z为属性集，Z=U-X-Y，下列关于平凡的多值依赖的叙述中，哪一条是正确的?______。

    A．若X→→Y，Z=Φ，则称X→→Y为平凡的多值依赖

    B．若X→→Y，Z≠Φ，则称X→→Y为平凡的多值依赖

    C．若X→Y，X→→Y，则称X→→Y为平凡的多值依赖

    D．若X→→Y，X→→Z，则称X→→Y为平凡的多值依赖


    正确答案：A

  • 第2题：

    设U为所有属性，X、Y、Z为属性集，Z=U-X—Y，下列关于平凡的多值依赖的叙述中，哪一条是正确的?

    A．若X→→Y，Z=，则称X→→Y为平凡的多值依赖

    B．若X→→Y，Z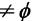，则称X一一为平凡的多值依赖

    C．若X→Y，X→→Y，则称X→→Y为平凡的多值依赖

    D．若X→→Y，X→→Z，则称X→→Y为平凡的多值依赖


    正确答案：A
    解析：本题是对函数多值依赖中的平凡的多值依赖定义的考查。如果x→Y，Z=，则称X→→Y称为平凡的多值依赖。对照题目中的4个选项可知，正确答案为选项A。

  • 第3题：

    设U为所有属性的集合，X、Y、Z为属性集，Z=U-X-Y。下列关于多值依赖的叙述中，正确的是（ ）。

    A)若X→→Y则X→→Z

    B)若X→→Y，则X→Y


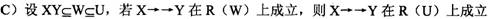
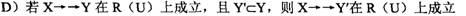    正确答案：A
    若X→→Y，而Z=Φ，则称X→→Y为平凡的多值依赖。若X→→Y在R(U)上成立，用Y'∈Y，我们不可以断言X→→Y'成立。设R是属性集U上的一个关系模式，X、Y是U的子集，Z=U-X-Y，多值依赖的性质有：①若X→→Y，则X→→Z，其中Z=U-X-Y，即多值依赖具有对称性。②若X→Y，则X→→Y，即函数依赖可以看作多值依赖的特殊情况。③设属性集之间的关系是XY∈W∈U，那么当X→→Y在R(U)上成立的时候，X→→Y在R(W)上也成立；反过来当X→→Y在R(W)上成立时，X→→Y在R(U)上不一定成立。④若X→→Y，且Y，∈Y，但不能断言X→→Y'也成立。因为多值依赖的定义中涉及了u中除x、Y之外的其余属性Z，考虑X→→Y，是否成立时涉及的其余的属性Z'=U-X-Y'比确定X→→Y成立时的其余属性Z=U-X-Y包含的属性列多，因此X→→Y'不一定成立。

  • 第4题：

    设U为所有属性，X, Y, Z为属性集，Z＝U-X-Y。若X→→Y,且Z＝，则称X→→Y为【 】的多值依赖。


    正确答案：平凡
    平凡

  • 第5题：

    设U是所有属性的集合，X、Y、Z都是u的子集，且Z=U—X—Y。下面关于多值依赖的叙述中，不正确的是（ ）o


    正确答案：C
    若X→→Y，而Z=Φ，则称X→→Y为平凡的多值依赖。若X→→Y在R(U)上成立，且Y’∈Y，我们不可以断言X→→Y’成立。设R是属性集U上的一个关系模式，X、Y是U的子集，Z=U-X-Y，多值依赖的性质有：①若X→→Y，则X→→Z，其中Z=U-X-Y，即多值依赖具有对称性。②若X→Y，则X→→Y，即函数依赖可以看作多值依赖的特殊情况。③设属性集之间的关系是XYEW∈U，那么当X→→Y在R(U)上成立的时候，X→→Y在R(W)上也成立；反过来当X→→Y在R(W)上成立时，X→→Y在R(U)上不一定成立。④若X→→Y，且Y’∈Y，但不能断言X→→Y也成立。因为多值依赖的定义中涉及了U中除X、Y之外的其余属性Z，考虑X→→Y，是否成立时涉及的其余的属性Z=U-X-Y’比确定X→→Y成立时的其余属性Z=U-X．Y包含的属性列多，因此X→→Y’不一定成立。

相关内容