设X=ab,Y=cd分别为2位二进制正整数,X>Y的逻辑表示式是( )。A.ac+aM+bcdB.ac+adb+bcdC.ad+abc+bcdD.ac+bcd+abd
题目
设X=ab,Y=cd分别为2位二进制正整数,X>Y的逻辑表示式是( )。
A.ac+aM+bcd
B.ac+adb+bcd
C.ad+abc+bcd
D.ac+bcd+abd
相似考题
更多“设X=ab,Y=cd分别为2位二进制正整数,X>Y的逻辑表示式是( )。A.ac+aM+bcdB.ac+adb+bcdC.ad+abc+bc ”相关问题
-
第1题:
逻辑变量x、Y进行逻辑“异或”(用⊕表示)运算的含义是:若x、Y取值相同(都为trlle或都为false),则x⊕Y值为false,否则x⊕Y的值为true c。用逻辑“与”(∧)、“或”(∨)、“非”(-)表示x⊕Y的式子为( )。
A.(X∧Y)∧(x∧Y)
B.(X∨Y) ∧(X∨Y)
C.(X∧Y)∨(x∧Y)
D.(X∨VY)∨(X∨Y)
正确答案:C
解析:异或是一个数学运算符,应用于逻辑运算。其运算法则为a异或b=a'b或ab'(a'为非a)。【总结与扩展】逻辑运算又称布尔运算,布尔用数学方法研究逻辑问题,成功地建立了逻辑演算。他用等式表示判断,把推理看做等式的变换。这种变换的有效性不依赖人们对符号的解释,只依赖于符号的组合规律。这一逻辑理论人们常称它为布尔代数。20世纪30年代,逻辑代数在电路系统上获得应用,随后,由于电子技术与计算机的发展,出现各种复杂的大系统,它们的变换规律也遵守布尔所揭示的规律。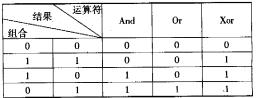
简单地说,And:同为真时为真;
0r:同为假时为假;
Xor:相同为假。 -
第2题:
1、X、Y均为四位二进制数,它们分别是一个逻辑电路的输入和输出。 设: 当 0≤X≤ 4时, Y=X+1 ;当 5≤X≤9 时,Y=X-1,且X不大于9。 (1)试列出该逻辑电路完整的真值表; (2)用卡诺图化简最简式; (3)用与非门实现该逻辑电路。
正确 -
第3题:
给定解释 I 为: 论域 D=正整数集合, f(x, y)=x+y, 谓词F(x, y)表示x=y, a=2。 那么在这个解释下,($x)("y)("z)F(f(y, z), x) 为真。
错误 -
第4题:
设X=ab,Y=cd分别为2位二进制正整数,x>Y的逻辑表示式是( )。
A.ac+abd+bcd
B.ac+adb+bcd
C.ad+abc+bcd
D.ac+bcd+abd
正确答案:D
-
第5题:
命题“有的人喜欢所有的花”的逻辑符号化表示为? 设D:全总个体域,F(x):x是花,M(x):x是人,H(x,y):x喜欢y
A.∀x(M(x)→∀y(F(y)→H(x,y)))
B.∀x(M(x)∧∀y(F(y)→H(x,y)))
C.∃x(M(x)→∀y(F(y)→H(x,y)))
D.∃x(M(x)∧∀y(F(y)→H(x,y)))
<img src='https://image.zhihuishu.com/zhs/doctrans/docx2html/202008/14d8488be9ce46ce827eb9eb578a8d04.png' width='142px' height='12px' />,其中,<img src='https://image.zhihuishu.com/zhs/doctrans/docx2html/202008/b2123a89c0494151b1379da97225926c.png' width='207px' height='10px' />
