itgle.com

设V1为无向连通图G的点割集，记G删除V1的连通分支个数为p(G- V1) = k，下列命题中一定为真的为A．k≥2B．k≥3C．k≤2D．k = 2

题目

设V1为无向连通图G的点割集，记G删除V1的连通分支个数为p(G- V1) = k，下列命题中一定为真的为

A．k≥2

B．k≥3

C．k≤2

D．k = 2

相似考题

1.在渔业生产上为获得持续最大捕捞量，海洋捕捞时，应使鱼类的种群数量保持在（ ）A．K/2B．K/3C．K/4D．K/5

2.阅读下列C程序和程序说明，将应填入(n)处的字句写在答题纸的对应栏内。【说明】用克鲁斯卡尔算法求解给定图的最小生成树。include ＜stdio. h＞include ＜stdlib. h＞define MAXN 30typedef struct{ int v1,v2; /*一条边依附的两个顶点*/int weight; /*边上的权值*/}EDGE;typedef struct{ int Vnum; /*图中的顶点数目*/EDGE e[MAXN*(MAXN-1)/2]; /*图中的边*/}Graph;typedef struct node{ /*用链表存储同一个连通分量的顶点*/int v;struct node *next;}Alist;void heapadjust(EDGE data[], int s, int m){ /*将元素序列data[s..m]调整为小顶堆, 堆顶元素(最小元素)为data[s]*/int j;EDGE t;t=data[s]; /*备份元素data[s], 为其找到适当位置后再插入*/for(j=2*s+1; j＜=m; j=j*2+1){/*沿值较小的子结点向下筛选*/if(j＜m &&(1)) ++j;if(!(t. weight＞data[j]. weight)) break;data[s]=data[j];s=j; /*用s记录待插入元素的位置(下标)*/}/*for*/data[s]=t; /*将备份元素插入由s所指出的插入位置*/}/*heapadjust*/int creat_graph(Graph *p) /*输入图中的顶点及边, 返回图中边的数目*/{ int k=0; /*记录图中边的数目*/int n;int v1,v2;int w;printf("vertex number of the graph:");scanf("%d", &n); /*输入图中的顶点数目*/if(n＜1) return 0;p-＞Vnum=n;do{ printf("edge(vertex1,vertex2,weight):");scanf("%d %d %d", &V1, &v2, &w);if(v1＞=0 && v1＜n && v2＞=0 && v2＜n){p-＞e[k]. v1=v1; p-＞e[k]. v2=v2; p-＞e[k]. weight=w;k++;}/*if*/}while(!( (2) ));return k; /*返回图中边的数目*/}/*creat_graph*/int kruskal(Graph G, int enumber, int tree[][3]){ /*用kruskal算法求无向连通图G的最小生成树, 图中边所得数目为enumber, *//*数组tree[][3]中存放生成树中边的顶点和边上的权值, 函数返回生成树的代价*/int i, k, m, c=0;int v1, v2;Alist *p, *q, *a[MAXN];for(i=0; i＜G．Vnum; ++i){ /*将每个连通分量中的顶点存放在一个单链表中*/a[i]=(Alist*)malloc(sizeof(Alist));if(!a[i]) {printf("\n mernory allocation error!");exit(0);}/*if*/a[i]-＞v=i; a[i]-＞next=NULL;}/*for*/for(i=enumber-1; i＞=0; --i)/*按照边上的权值建立小顶堆*/heapadjust( (3) );k=G. Vnum; /*k用于计算图中的连通分量数目*/m=enumber-1;i=0;do{v1=G. e[0]. v1; v2=G. e[0]. v2;p=a[v1];while(p && p-＞v!=v2){ /*判断当前选择的边的顶点是否在一个连通分量中*/q=p; p=p-＞next;}if(!p){ /*当前边的顶点不在一个连通分量中*/p=q;p-＞next=a[G. e[0]. v2];&nb

3.如果数字显示仪器的分辨力为δx，则区间半宽，可设为均匀分布，查表（）A.k=0.5B.k=3C.k=2D.k=0.29

4.阅读下列函数说明和C函数，将应填入(n)处的字句写在对应栏内。[说明]Kruskal算法是一种构造图的最小生成树的方法。设G为一无向连通图，令T是由G的顶点构成的于图，Kmskal算法的基本思想是为T添加适当的边使之成为最小生成树：初始时，T中的点互相不连通；考察G的边集E中的每条边，若它的两个顶点在T中不连通，则将此边添加到T中，同时合并其两顶点所在的连通分量，如此下去，当添加了n-1条边时，T的连通分量个数为1，T便是G的一棵最小生成树。下面的函数void Kruskal(EdgeType edges[],int n)利用Kruskal算法，构造了有n个顶点的图 edges的最小生成树。其中数组father[]用于记录T中顶点的连通性质：其初值为father[i]=-1 (i=0,1,…,n-1)，表示各个顶点在不同的连通分量上；若有father[i]=j，j＞-1，则顶点i，j连通；函数int Find(int father[],int v)用于返回顶点v所在树形连通分支的根结点。[函数]define MAXEDGE 1000typedef struct{ int v1;int v2;}EdgeType;void Kruskal(EdgeType edges[],int n){ int father[MAXEDGE];int i,j,vf1,vt2;for(i=0;i＜n;i+ +) father[i]=-1;i=0;j=0;while(i＜MAXEDGE && j＜(1)){ vf1=Find(father,edges[i].v1);vf2=Find(father,edges[i].v2);if((2)){(3)=vf1;(4);printf("%3d%3d\n",edges[i].v1,edges[i].v2);}(5);}}int Find(int father[],int v){ int t;t=v;while(father[t]＞=0) t=father[t];return(t);}

更多“设V1为无向连通图G的点割集，记G删除V1的连通分支个数为p(G- V1) = k，下列命题中一定为真的为A．k≥2B．k≥3C．k≤2D．k = 2”相关问题

  • 第1题：

    设G1=(V1,E1)和G2=(V2,E2)为两个图,如果V1ÍV2,E1ÍE2则称()。

    A、G1是G2的子图

    B、G1是G2的连通分量


    参考答案：A

  • 第2题：

    图 G 的最小支撑树中从 V1 到 Vn 的通路一定是图 G 从 V1 到 Vn 的最短路。 ()

    此题为判断题(对，错)。


    正确答案:错误

  • 第3题：

    下列命题正确的是(58)。

    A．G为n阶无向连通图，如果G的边数m≥n-1，则G中必有圈

    B．二部图的顶点个数一定是偶数

    C．若无向图C的任何两个不相同的顶点均相邻，则G为哈密尔顿图

    D．3-正则图的顶点个数可以是奇数，也可以是偶数


    正确答案：C
    解析：n阶无向连通图至少有n-1条边，但n阶无向连通图不一定有圈，所以A错误。二部图顶点个数也可以为奇数，可知D错误。由握手定理可知，n阶k-正则图中，边数m=kn/2，因而当k为奇数时，n必为偶数。所以D错误。所以选C。

  • 第4题：

    若非连通无向图G含有21条边，则G的顶点个数至少为 ( )

    A．7

    B．8

    C．21

    D．22


    正确答案：B

  • 第5题：

    设有向图G=(V，E)和G′-(V′，E′).如(G′)是G生成树，下面说法中不正确的是()

    A.G′为G的连通分量
    B.G′为G的无环子图
    C.G′为G的子图
    D.G′为G的极小连通子图且V′=V

    答案：A
    解析：
    B项、D项都是生成树的特点，而A项为概念错误：G′为连通图而非连通分量，图的连通分量是指无向图中的极大连通子图。

  • 第6题：

    图G的邻接矩阵如下图所示（顶点依次表示为v0、v1、v2、v3、v4、v5），G是（请作答此空）。对G进行广度优先遍历（从v0开始），可能的遍历序列为（ ）。


    A.无向图
    B.有向图
    C.完全图
    D.强连通图

    答案：B
    解析：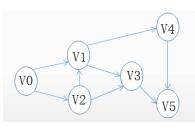

  • 第7题：

    设无向图G=（V，E）和G’=（V’，E’），如果G’是G的生成树，则下面的说法中错误的是（）。

    • A、G’为G的子图
    • B、G’为G的连通分量
    • C、G’为G的极小连通子图且V=V’
    • D、G’是G的一个无环子图

    正确答案:B

  • 第8题：

    温度不变时，气体的体积(V)与压强(P)的关系是（　）

    • A、V1／V2=P2／P1
    • B、V1／V2=P1／P2
    • C、V1=K·V2P1／P1、2
    • D、V1=K·V2P2／P1
    • E、V1·V2=P1·P2

    正确答案:A

  • 第9题：

    设G1=（V1，E1）和G2=（V2，E2）为两个图，如果V1V2，E1E2则称（）。

    • A、G1是G2的子图
    • B、G2是G1的子图
    • C、G1是G2的连通分量
    • D、G2是G1的连通分量

    正确答案:A

  • 第10题：

    实际液体在粗细均匀的水平管中层流时，管中1点比2点距流源近， 两点的流速与压强分别是：（）

    • A、v1＞v2，p1＞p2
    • B、v1＞v2，p1=p2
    • C、v1=v2，p1=p2
    • D、v1=v2，p1＞p2

    正确答案:D

  • 第11题：

    单选题
    设无向图G=（V，E）和G’=（V’，E’），如果G’是G的生成树，则下面的说法中错误的是（）。
    A

    G’为G的子图

    B

    G’为G的连通分量

    C

    G’为G的极小连通子图且V=V’

    D

    G’是G的一个无环子图


    正确答案： A
    解析： 暂无解析

  • 第12题：

    填空题
    设G为具有N个顶点的无向连通图，则G至少有（）条边。

    正确答案： N-1
    解析： 暂无解析

  • 第13题：

    将1molN2和1molO2放在一密闭的容器中,发生了如下的气相反应N2＋O2===2NO,则此系统的组分数和自由度数为()。

    A.K=1，f=2

    B.K=2，f=3

    C.K=3，f=4

    D.K=1，f=1


    正确答案：A

  • 第14题：

    设无向图G=(P，L)，P={v1，v2，v3，v4，v5，v6}，L={(v1，v2)，(v2，v2)，(v2，v4)，(v4，v5)，(v3，v4)，(v1，v3)，(v3，v1)}。G中奇数度顶点的个数是(60)。

    A．2

    B．3

    C．4

    D．5


    正确答案：C
    解析：C中各点的度如下：dG(v1)=3，dG(v2)=4，dG(v3)=3，dG(v4)=3，dG(v5)=1，dG(v6)=0。奇数度顶点的个数为4。

  • 第15题：

    设V'和E'分别为无向连通图G的点割集和边割集，下面的说法中正确的是( )。

    Ⅰ．G-E'的连通分支数p(G-E')=2

    Ⅱ．G-V'的连通分支数p(G-V')一定等于G-E'的连通分支数p(G-E')

    Ⅲ．G-V'的连通分支数p(G-V')≥2

    A．Ⅰ和Ⅱ

    B．Ⅰ和Ⅲ

    C．Ⅱ

    D．没有


    正确答案：B

  • 第16题：

    设无向图G=(V，E)和G′=(V′，E′)，如果G′是G的生成树，则下面的说法中错误的是()。

    A.G′为G的极小连通子图且V=V′
    B.G′是G的一个无环子图
    C.G′为G的子图
    D.G′为G的连通分量

    答案：D
    解析：
    连通分量是无向图的极大连通子图，其中极大的含义是将依附于连通分量中顶点的所有边都加上，所以，连通分量中可能存在回路。

  • 第17题：

    图G的邻接矩阵如下图所示（顶点依次表示为v0、v1、v2、v3、v4、v5），G是（　）。对G进行广度优先遍历（从v0开始），可能的遍历序列为（请作答此空）。


    A.v0、v1、v2、v3、v4、v5
    B.v0、v2、v4、 v5、v1、v3
    C.v0、v1、v3、v5、v2、v4
    D.v0、v2、v4、v3、v5、v1

    答案：A
    解析：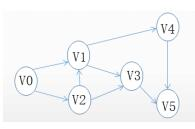

  • 第18题：

    已知无向图G描述如下： G=（V，E） V={V1，V2，V3，V4，V5} E={（V1，V2），（V1，V4），（V2，V4），（V3，V4），（V2，V5），（V3，V4），（V3，V5）} 写出每个顶点的度。
    V1、V2、V3、V4、V5的度分别为：2，3，2，3，2。
    略

  • 第19题：

    温度不变时，气体的体积（V）与压强（P）的关系是（）

    • A、V1/V2=P2/P1
    • B、V1/V2=P1/P2
    • C、V1=K·V2P1/P1、2
    • D、V1=K·V2P/P1
    • E、V1·V2=P1.P2

    正确答案:A

  • 第20题：

    一物体从t0=0时刻开始做匀减速直线运动，发生一段位移所用时间为t，设位移中点时刻为t1，速度为v1，时间中点时刻为t2，速度为v2，下列说法正确的是（）

    • A、t1=t2，v1=v2
    • B、t1＞t2，v1＞v2
    • C、t1＜t2，v1＜v2
    • D、t1＜t2，v1＞v2

    正确答案:D

  • 第21题：

    设G为具有N个顶点的无向连通图，则G至少有（）条边。


    正确答案:N-1

  • 第22题：

    单选题
    设G1=（V1，E1）和G2=（V2，E2）为两个图，如果V1V2，E1E2则称（）。
    A

    G1是G2的子图

    B

    G2是G1的子图

    C

    G1是G2的连通分量

    D

    G2是G1的连通分量


    正确答案： A
    解析： 暂无解析

  • 第23题：

    问答题
    已知无向图G描述如下： G=（V，E） V={V1，V2，V3，V4，V5} E={（V1，V2），（V1，V4），（V2，V4），（V3，V4），（V2，V5），（V3，V4），（V3，V5）} 写出每个顶点的度。

    正确答案： V1、V2、V3、V4、V5的度分别为：2，3，2，3，2。
    解析： 暂无解析

相关内容