itgle.com

设A与B是相互独立的事件，已知P(A)=1/3，P(B)=1/4，则P(A*B)=()。A:1/12 B:1/4 C:1/3 D:7/12

题目
设A与B是相互独立的事件，已知P(A)=1/3，P(B)=1/4，则P(A*B)=()。

A:1/12
B:1/4
C:1/3
D:7/12
相似考题

1.设A、B为两个随机事件，则下列叙述正确的有( )。A．A与B互不相容，则P(A∪B)=P(A)+P(B)B．A与B相互独立，则P(AB)=P(A)P(B)C．A与B为任意事件，则P(A∪B)=1-P(A)P(B)D．A与B为任意事件，则P(A∪B)=P(A)+P(B)-P(A)P(B)E．A、B为任意事件，则P(A∪B)=P(A)+P(B)-P(AB)

2.设A、B是两个事件,P(A)=1/2,P(B)=1/3,P(AB)=1/4,则P(A∪B)为________。A．5/12B．1C．3/4D．7/12

3.设随机事件A与B相互独立,P(4)=0.2,P(B)=0.4,则P(AIB)=()。A、0B、0.2C、0.4D、1

4.设A与B是相互独立的事件，已知P(A)=1/3，P(B)=1/4，则P(AxB)=( )。A．40555B．40547C．40546D．40736

更多“设A与B是相互独立的事件，已知P(A)=1/3，P(B)=1/4，则P(A*B)=()。”相关问题

  • 第1题：

    已知P(A)=0.3,P(B)=0.5,则当事件A,B相互独立时,P(A＋B)=( ),P(A|B)=( )。


    参考答案：0.65、0.3

  • 第2题：

    设事件A,B相互独立,P(A)=0.3,且P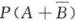=0.7,则P(B)=_______.


    答案：
    解析：

  • 第3题：

    设事件A与B相互独立，且P(A)=1/2，P(B)=1/3,则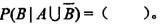

    A. 5/6 B. 1/6 C. 1/3 D.1/5


    答案：D
    解析：

  • 第4题：

    设事件A，B满足P（A+B）=P（A）+P（B），则（）.

    • A、A与B互不相容
    • B、A与B相互独立
    • C、A与B相互对立
    • D、P（A-B）=P（A）

    正确答案:D

  • 第5题：

    设A、B、C两两相互独立，满足ABC=Φ，P（A）=P（B）=（C）<1/2，且已知P（A∪B∪C）=9/16，则P（A）=（）。


    正确答案:1/4

  • 第6题：

    设事件A与B相互独立．已知P（A）=0.3，P（A+B）=0.65，则P（B）等于（）．

    • A、0.3
    • B、0.35
    • C、0.5
    • D、0.95

    正确答案:C

  • 第7题：

    设A与B是相互独立的事件，已知P（A）=1/2，P（B）=1/3，则P（A+B）=（）。

    • A、1/2
    • B、1/3
    • C、5/6
    • D、2/3

    正确答案:D

  • 第8题：

    设A、B为两事件，P（A）=0.4，P（B）=0.3，如果A与B相互独立，则：P（A－B）=（）；如果A与B互斥，则P（A－B）=（）。


    正确答案:0.28；0.4

  • 第9题：

    单选题
    设A、B、C是两两相互独立且三事件不能同时发生的事件，且P（A）＝P（B）＝P（C）＝x，则使P（A∪B∪C）取最大值的x为（　　）。
    A

    1

    B

    1/2

    C

    1/3

    D

    1/4


    正确答案： D
    解析：
    P（A∪B∪C）＝P（A）＋P（B）＋P（C）－P（AB）－P（AC）－P（BC）＋P（ABC）＝P（A）＋P（B）＋P（C）－P（A）P（B）－P（A）P（C）－P（B）P（C）＋0＝3x－3x2，设f（x）＝3x－3x2，则f′（x）＝3（1－2x）＝0，解得x＝1/2，f″（1/2）＝－6＜0，故x＝1/2为最大值点。

  • 第10题：

    单选题
    设A与B是相互独立的事件，已知P（A）=1/2，P（B）=1/3，则P（A+B）=()。
    A

    1/2

    B

    1/3

    C

    5/6

    D

    2/3


    正确答案： D
    解析： AB相互独立=P（AB）=P（A）P（B），所以，P（A+B）=P（A）+P（B）

  • 第11题：

    单选题
    设事件A与B相互独立.已知P（A）=0.3，P（A+B）=0.65，则P（B）等于（）.
    A

    0.3

    B

    0.35

    C

    0.5

    D

    0.95


    正确答案： D
    解析： 暂无解析

  • 第12题：

    填空题
    设两两相互独立的三个事件A、B、C满足条件ABC＝∅，P（A）＝P（B）＝P（C）＜1/2，且已知P（A∪B∪C）＝9/16，则P（A）＝____。

    正确答案： 1/4
    解析：
    P（A∪B∪C）＝P（A）＋P（B）＋P（C）－P（AB）－P（AC）－P（BC）＋P（ABC）＝3P（A）－3[P（A）]2＋0＝9/16（因ABC＝∅，故P（ABC）＝0），解得P（A）＝1/4，P（A）＝3/4（舍去）。

  • 第13题：

    已知事件A与B为相互独立事件，则P(AB)=()．

    A.P(A)+P(B)
    B.P(A)-P(B)
    C.P(A)+P(B)-P(A)P(B)
    D.P(A)P(B)

    答案：D
    解析：
    依据事件相互独立的定义，可知选项D正确．

  • 第14题：

    设两两相互独立的三事件A，B和C满足条件ABC=，P(A)=P(B)=P(C)<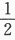，且已知P(A∪B∪C)=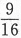，则P(A)=________.


    答案：
    解析：
    利用加法公式P(A∪B∪C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC)再加上两两独立性质解得P(A)=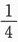，其实题设条件P(A)<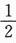没有必要，因为求解方程中有一个增根P(A)=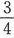是不可能要的，这一点可从P(A)≤P(A∪B∪C)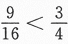直接得出

  • 第15题：

    设随机事件A与B相互独立，且P（A）=0.4，P（B）=0.5，则P（AB）=（）


    正确答案:0.2

  • 第16题：

    设A，B为随机事件，已知P（A）=1/4，P（B∣A）=1/2，P（A∣B）=1/3，则P（AUB）=（）

    • A、1/8
    • B、1/4
    • C、3/8
    • D、1/2

    正确答案:D

  • 第17题：

    设事件A，B满足P（A+B）=P（A）+P（B），则（）．

    • A、A与B互不相容
    • B、A与B相互独立
    • C、A与B相互对立
    • D、D.P（A-B.=P

    正确答案:D

  • 第18题：

    设随机变量X与Y相互独立，已知P（X≤1）=p，P（Y≤1）=q，则P（max（X，Y）≤1）等于（）．

    • A、p+q
    • B、pq
    • C、p
    • D、q

    正确答案:B

  • 第19题：

    设事件A、B相互独立，且P（A）＝0.4；P（B）＝0.05，则P（AB）＝（）；P（A＋B）＝（）。


    正确答案:0.02；0.43

  • 第20题：

    单选题
    设0＜P（A）＜1，0＜P（B）＜1，P（A|B）＋P（A(＿)|B(＿)）＝1，则（　　）。
    A

    事件A与B互不相容

    B

    事件A与B相互独立

    C

    事件A与B相互对立

    D

    事件A与B互不独立


    正确答案： C
    解析：
    根据题意P（A|B）＝1－P（A(＿)|B(＿)）＝P（A|B(＿)），故：
    P（AB）/P（B）＝P（AB(＿)）/P（B(＿)）
    P（AB）P（B(＿)）＝P（B）P（AB(＿)）
    P（AB）[1－P（B）]＝P（B）P（AB(＿)）
    P（AB）－P（AB）P（B）＝P（B）P（AB(＿)）
    P（AB）＝P（B）[P（AB）＋P（AB(＿)）]＝P（B）P（A）
    故事件A与B相互独立。

  • 第21题：

    单选题
    设随机事件A、B、C相互独立，则（　　）。
    A

    P（A∪B）P（C）＝[P（A）＋P（B）]P（C）

    B

    P（A(＿)∪B(＿)∪C(＿)）＝1－P（A(＿)）－P（B(＿)）－P（C(＿)）

    C

    事件A∪B与事件C相互独立

    D

    以上都不对


    正确答案： C
    解析：
    P[（A∪B）C]＝P（AC∪BC）＝P（AC）＋P（BC）－P（ABC）＝P（A）P（C）＋P（B）P（C）－P（A）P（B）P（C）＝[P（A）＋P（B）－P（AB）]P（C）＝P（A∪B）P（C）。

  • 第22题：

    单选题
    设A、B是两个相互独立事件，P(A)=1／2，P(B)=1／3，则P(AB)为(　　)。
    A

    7／12

    B

    1

    C

    1／6

    D

    3／8


    正确答案： B
    解析： 暂无解析

  • 第23题：

    单选题
    设随机变量X与Y相互独立，已知P（X≤1）=p，P（Y≤1）=q，则P（max（X，Y）≤1）等于（）．
    A

    p+q

    B

    pq

    C

    p

    D

    q


    正确答案： B
    解析： 随机事件{max（X，Y）≤1}={X≤1，Y≤1}，因此，由乘法公式得到P（max（X，Y）≤1）=P（X≤1，y≤1）=P（X≤1）P（Y≤1）=pq.故选（B）.本题中{max（X，Y）≤1}可以分解成两个简单事件的积，类似地，{max（X，Y）≥1}={X≥1}∪{Y≥1}，{min（X，Y）≥1}={X≥1，y≥1}，{min（X，Y）≤1}={X≤1}∪{Y≤1}.例如，由本题所给条件可以算得（按加法公式与乘法公式）：P（min（X，Y）≤1）=P（{x≤1}∪{Y≤1}）=P（X≤1）+P（Y≤1）-P（X≤1，Y≤1）=p+q-P（X≤1）P（Y≤1）=p+q-pq.

相关内容