itgle.com

已知二叉树T的结点形式为(lling,data,count,rlink),在树中查找值为X的结点,若找到,则记数(count)加1,否则,作为一个新结点插入树中,插入后仍为二叉排序树,写出其非递归算法。

题目
已知二叉树T的结点形式为(lling,data,count,rlink),在树中查找值为X的结点,若找到,则记数(count)加1,否则,作为一个新结点插入树中,插入后仍为二叉排序树,写出其非递归算法。

相似考题

1.阅读以下说明和C语言函数，将应填入(n)处。[说明]二叉排序树或者是一棵空树，或者是具有如下性质的二叉树：若它的左子树非空，则左子树上所有结点的值均小于根结点的值；若它的右子树非空，则右子树上所有结点的值均大于根结点的值；左、右子树本身就是两棵二义排序树。函数insert_BST(char *str)的功能是：对给定的字符序列按照ASCⅡ码值大小关系创建二叉排序树，并返回指向树根结点的指针。序列中重复出现的字符只建一个结点，并由结点中的Count域对字符的重复次数进行计数。二叉排序树的链表结点类型定义如下：typedef struct BSTNode{char Elem; /*结点的字符数据*/int Count; /*记录当前字符在序列中重复出现的次数*/struct BSTNode *Lch,*Rch; /*接点的左、右子树指针*/}*BiTree;[函数]BiTree insert_BST(char *str){ BiTree root,parent,p;char (1); /*变量定义及初始化 */root=(BiTree)malloc(sizeof(struct BSTNode));if(!root||*s=='\0') return NULL;root-＞Lch=root-＞Rch=NULL; foot-＞Count=1; root-＞Elem=*s++;for(; *s!='\0';s++) {(2); parent=NULL;while (p){ /*p从树跟结点出发查找当前字符*s所在结点 */parent = p;if(*s==p-＞Elem)/*若树中已存在当前字符结点，则当前字符的计数值加1*/{p-＞Count++; break;}else /*否则根据字符*s与结点*p中字符的关系，进入*p的左子树或右子树*/if (*s＞p-＞Elem) p=p-＞Rch;else p=p-＞Lch;}/*while*/if( (3)) {/* 若树中不存在字符值为*s的结点，则申请结点并插入树中 */p=(BiTree)malloc(sizeof(struct BSTNode));if(!p)return NULL;p-＞Lch=p-＞Rch=NULL; p-＞Count=1; p-＞Elem=*s;/*根据当前字符与其父结点字符值的大小关系，将新结点作为左子树或右子树插入*/if(p-＞Elem＞parent-＞Elem) (4)=p;else (5)=p;}}/*for*/return root；}

2.已知二叉排序树采用二叉链表存储结构,根结点的指针为T,链结点的结构为(lchild,data,rchild),其中lchild,rchild分别指向该结点左、右孩子的指针,data域存放结点的数据信息。请写出递归算法,从小到大输出二叉排序树中所有数据值>=x的结点的数据。要求先找到第一个满足条件的结点后,再依次输出其他满足条件的结点。

3.阅读以下说明和C代码，填补代码中的空缺，将解答填入答题纸的对应栏内。 【说明】 二叉查找树又称为二叉排序树，它或者是一棵空树，或者是具有如下性质的二叉树。 （1）若它的左子树非空，则左子树上所有结点的值均小于根结点的值。 （2）若它的右子树非空，则右子树上所有结点的值均大于根结点的值。 （3）左、右子树本身就是两棵二叉查找树。 二叉查找树是通过依次输入数据元素并把它们插入到二叉树的适当位置上构造起来的，具体的过程是：每读入一个元素，建立一个新结点，若二叉查找树非空，则将新结点的值与根结点的值相比较，如果小于根结点的值，则插入到左子树中，否则插入到右子树中；若二叉查找树为空，则新结点作为二叉查找树的根结点。 根据关键码序列{46，25，54，13，29，91}构造一个二叉查找树的过程如图4-1所示。设二叉查找树采用二叉链表存储，结点类型定义如下： typedef int KeyType； typedef struct BSTNode{ KeyType key； struct BSTNode *left,*right； }BSTNode,*BSTree； 图4-1(g)所示二叉查找树的二叉链表表示如图4-2所示。图4-2 函数int InsertBST(BSTree *rootptr,KeyType kword)功能是将关键码kword插入到由rootptr指示出根结点的二叉查找树中，若插入成功，函数返回1，否则返回0。【C代码】 int lnsertBST(BSTree*rootptr，KeyType kword) /*在二叉查找树中插入一个键值为kword的结点，若插入成功返回1，否则返回0； *rootptr为二叉查找树根结点的指针 */ { BSTree p,father; (1) ; /*将father初始化为空指针*/ p=*rootptr; /*p指示二叉查找树的根节点*/ while(p&& （2） ){ /*在二叉查找树中查找键值kword的结点*/ father=p; if(kword＜p-＞key) p=p-＞left； else p=p-＞right； } if( (3) )return 0; /*二叉查找树中已包含键值kword，插入失败*/ p=(BSTree)malloc( (4) ); /*创建新结点用来保存键值kword*/ If(!p)return 0; /*创建新结点失败*/ p-＞key=kword； p-＞left=NULL； p-＞right=NULL； If(!father) (5) =p； /*二叉查找树为空树时新结点作为树根插入*/ else if(kword＜father-＞key) (6) ； /*作为左孩子结点插入*/ else (7) ； /*作右孩子结点插入*/ return 1； }/*InsertBST*/

4.若二叉排序树非空,则新结点的值和根结点比较,若小于根结点,则插入到右子树;否则插入到左子树。()此题为判断题(对，错)。

更多“已知二叉树T的结点形式为(lling,data,count,rlink),在树中查找值为X的结点,若找到,则记数(count)加1,否则,作为一个新结点插入树中,插入后仍为二叉排序树,写出其非递归算法。 ”相关问题

  • 第1题：

    试题三（共15分）

    阅读以下说明和C函数，填充函数中的空缺，将解答填入答题纸的对应栏内。

    【说明】

    函数Insert _key (*root,key)的功能是将键值key插入到*root指向根结点的二叉查找树中（二叉查找树为空时*root为空指针）。若给定的二叉查找树中已经包含键值为key的结点，则不进行插入操作并返回0；否则申请新结点、存入key的值并将新结点加入树中，返回l。

    提示：

    二叉查找树又称为二叉排序树，它或者是一棵空树，或者是具有如下性质的二叉树：

    ●若它的左子树非空，则其左子树上所有结点的键值均小于根结点的键值；

    ●若它的右子树非空，则其右子树上所有结点的键值均大于根结点的键值；

    ●左、右子树本身就是二叉查找树。

    设二叉查找树采用二叉链表存储结构，链表结点类型定义如下：

    typedef struct BiTnode{

    int key _value; ／*结点的键值，为非负整数*／

    struct BiTnode *left,*right; ／*结点的左、右子树指针*／

    }BiTnode, *BSTree；

    【C函数】

    int Insert _key( BSTree *root,int key)

    {

    BiTnode *father= NULL,*p=*root, *s;

    while( (1)＆＆key!=p->key_value){／*查找键值为key的结点*／

    father=p；

    if（key< p->key_value）p= (2) ； ／*进入左子树*／

    else p= (3) ； ／木进入右子树*／

    }

    if (p) return 0； ／*二叉查找树中已存在键值为key的结点，无需再插入*／

    s= (BiTnode *)malloc( (4) )；／*根据结点类型生成新结点*／

    if (!s) return -1;

    s->key_value= key; s->left= NULL; s->right= NULL;

    if( !father)

    (5) ； ／*新结点作为二叉查找树的根结点*／

    else ／*新结点插入二叉查找树的适当位置*／

    if( key< father->key_value)father->left = s;

    elsefather->right = s;

    retum 1：

    }


    正确答案：
    (1)p   
    (2)p->left   
    (3) p->right  
    (4) sizeof(BiTnode)   
    (5)  *root=s

  • 第2题：

    在二叉排序树中插入一个新结点，总是作为叶子结点插入。


    错误

  • 第3题：

    41、在二叉排序树中插入一个新结点，总是作为叶子结点插入。


    错误

  • 第4题：

    阅读以下说明和C代码，填补代码中的空缺，将解答填入答题纸的对应栏内。【说明】二叉查找树又称为二叉排序树，它或者是一棵空树，或者是具有如下性质的二叉树。（1）若它的左子树非空，则左子树上所有结点的值均小于根结点的值。（2）若它的右子树非空，则右子树上所有结点的值均大于根结点的值。（3）左、右子树本身就是两棵二叉查找树。二叉查找树是通过依次输入数据元素并把它们插入到二叉树的适当位置上构造起来的，具体的过程是：每读入一个元素，建立一个新结点，若二叉查找树非空，则将新结点的值与根结点的值相比较，如果小于根结点的值，则插入到左子树中，否则插入到右子树中；若二叉查找树为空，则新结点作为二叉查找树的根结点。根据关键码序列{46，25，54，13，29，91}构造一个二叉查找树的过程如图4-1所示。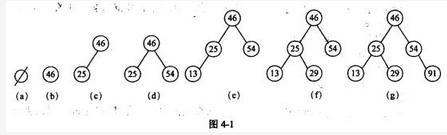

    设二叉查找树采用二叉链表存储，结点类型定义如下：

    typedef int KeyType；typedef struct BSTNode{KeyType key；struct BSTNode *left,*right；}BSTNode,*BSTree；

    图4-1(g)所示二叉查找树的二叉链表表示如图4-2所示。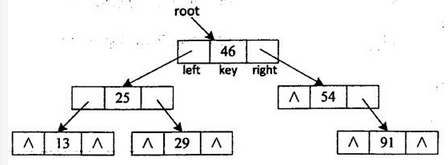

    函数int InsertBST(BSTree *rootptr,KeyType kword)功能是将关键码kword插入到由rootptr指示出根结点的二叉查找树中，若插入成功，函数返回1，否则返回0。【C代码】

    int lnsertBST(BSTree*rootptr，KeyType kword)/*在二叉查找树中插入一个键值为kword的结点，若插入成功返回1，否则返回0；*rootptr为二叉查找树根结点的指针*/{BSTree p,father;(1) /*将father初始化为空指针*/p=*rootptr; /*p指示二叉查找树的根节点*/while(p&&（2）){ /*在二叉查找树中查找键值kword的结点*/father=p;if(kword＜p-＞key)p=p-＞left；elsep=p-＞right；}if((3))return 0; /*二叉查找树中已包含键值kword，插入失败*/ p=(BSTree)malloc((4)); /*创建新结点用来保存键值kword*/If(!p)return 0; /*创建新结点失败*/p-＞key=kword；p-＞left=NULL；p-＞right=NULL； If(!father)(5) =p； /*二叉查找树为空树时新结点作为树根插入*/elseif(kword＜father-＞key)(6)；/*作为左孩子结点插入*/else(7)；/*作右孩子结点插入*/return 1；}/*InsertBST*/


    答案：
    解析：
    father=(void*)0keyword!=p-keypsizeof(BSTNode)*rootptrfather-left=pfather-right=p

  • 第5题：

    二叉排序树的基本运算，完成如下两个函数 bool InsertBST（bstree *pt,ElementType X);//在以*pt为根结点的二叉排序树中，插入一个关键字为X的结点，返回二叉排序树的根结点，若存在关键字为X的结点，不插入并返回false,否则插入该结点，并返回true bstree SearchBST（bstree t,ElementType X);//在以t为根结点的二叉排序树中，查找一个关键字为X的结点，若不存在关键字为X的结点，返回NULL，否则返回该结点的指针。


    算术

相关内容