某工程单代号搭接网络计划如下图所示,节点中下方数字为该工作的持续时间,其中关键工作是( )。A、工作AB、工作BC、工作CD、工作DE、工作E
题目
某工程单代号搭接网络计划如下图所示,节点中下方数字为该工作的持续时间,其中关键工作是( )。

A、工作A
B、工作B
C、工作C
D、工作D
E、工作E

A、工作A
B、工作B
C、工作C
D、工作D
E、工作E
相似考题
更多“某工程单代号搭接网络计划如下图所示,节点中下方数字为该工作的持续时间,其中关键工作是( )。 ”相关问题
-
第1题:
某工程单代号网络计划如下图所示,节点中下方数字为该工作的持续时间,其中的关键工作有( )。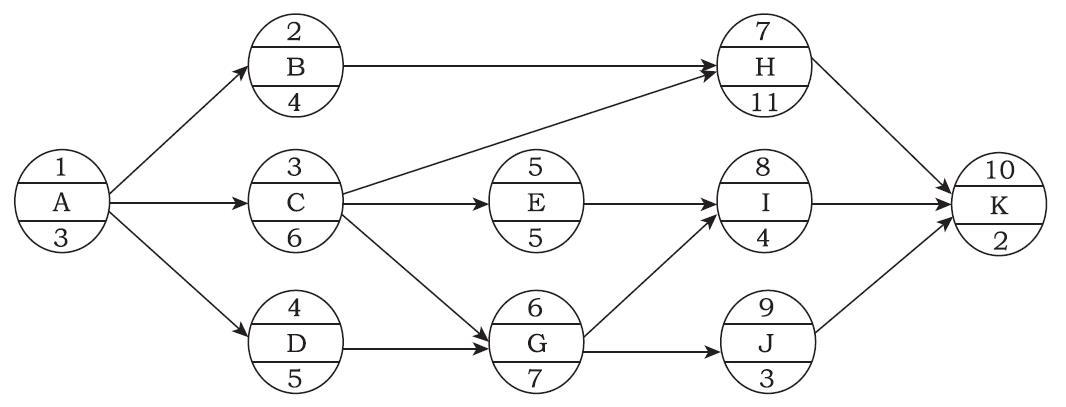
A、工作A
B、工作B
C、工作C
D、工作D
E、工作E答案:A,C解析:本题考查的是单代号网络计划时间参数的计算。单代号网络计划可以利用相邻两项工作之间的时间间隔来判定关键线路。即从网络计划的终点节点开始,逆着箭线方向依次找出相邻两项工作之间的时间间隔为零的线路就是关键线路。关键线路为A→C→G→I→K和A→C→H→K。 -
第2题:
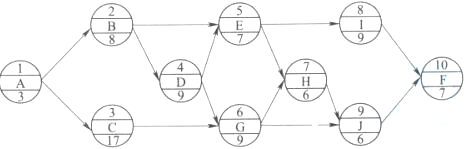
某分部工程单代号网络计划如下图所示,节点中下方数字为该工作的持续时间(单位:天),其关键线路有( )条。
 A:1
A:1
B:2
C:3
D:4答案:B解析:2019版教材P131
关键路线是持续时间最长的线路,因此,先列举网络的线路,再计算各线路的时间,时间最长的就是关键路线。本题的线路包括:ABEIF,ABEHJF,ABDEIF,ABDEHJF,ABDGHJF,ABDGJF,ACGHJF,ACGJF,他们的持续时间分别为:34,37,43,46,48,42,48,42。当然,本题也可以按教材的解法对整个网络进行计算,但这样太麻烦,而且没有必要。
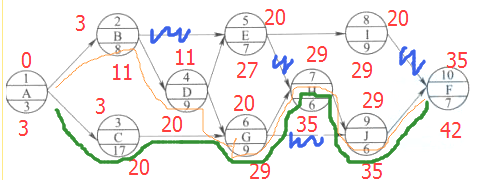
-
第3题:
某工程单代号搭接网络计划如图3-14所示,节点中下方数字为该工作的持续时间,其中的关键工作为()。 A.工作A、工作C和工作E
A.工作A、工作C和工作E
B.工作B、工作D和工作F
C.工作C、工作E和工作F
D.工作B、工作E和工作F答案:B解析:2020教材P79-83
首先根据已知条件,算出各工作的最早开始时间和最早完成时间;第二步计算相邻两项工作之间的时间间隔;第三步利用相邻两项工作之间的时间间隔来判定关键线路。关键线路上的工作即为关键工作。各工作的最早开始时间和最早完成时间如下:
(1)ESA=0,EFA=6。
(2)根据FTF=1,EFB=7,ESB=7-8=-1,显然不合理。为此,应将工作B与虚拟工作S(起点节点)相连,重新计算工作B的最早开始时间和最早完成时间得:ESB=0,EFB=8。
(3)根据STF=14,EFC=14,ESC=2。
(4)根据FTS=10,ESD=8+10=18,EFD=18+5=23。
(5)首先根据FTF=6,EFE=14+6=20,ESE=20-7=13,其次根据STS=4,ESE=4,EFE=11,取大值,ESE=13,EFE=20。
(6)根据STS=4,ESF=22,EFF=26,根据STF=6,ESF=19-4=15,EFF=13+6=19,所以取大值ESF=22,EFF=26,工期为26。
计算相邻两项工作之间的时间间隔:
LAGA,B=EFS(=8)-EFA(=6)-1=1;
LACB,D=ESD(=18)-EFB(=8)-10=0;LAGD,F=ESF(=22)-ESD(=18)-4=0。
因为B工作是和S虚工作相连的,所以SBDF是一条关键线路。
LAGB,E=ESE(=13)-ESB(=0)-4=9;
LAGA,C=EFC(=14)-ESA(=0)-14=0;
LAGC,E=EFE(=20)-EFC(=14)-6=0;
LAGE,F=EFF(=26)-ESE(=13)-6=7。
工作B的最早开始时间为0,所以它也是一个起始工作。根据“从搭接网络计划的终点开始,逆着箭线方向依次找出相邻两项工作之间时间间隔为零的线路就是关键线路。”其关键线路为BDF。所以只有BDF是关键线路。 -
第4题:
某工程单代号搭接网络计划如图341所示,节点中下方数字为该工作的持续时间,其中的关键工作有()。 A.工作A
A.工作A
B.工作B
C.工作C
D.工作D
E.工作E答案:A,B,E解析:2020教材P79-83
本题考查的是单代号搭接网络计划。
(1)ESA=0,EFA=0+4=4;
(2)EFB=ESA+STFA,B=0+4=4,ESB=4-3=1:
(3)ESC=ESA+STSA,C=0+2=2;
(4)C→E;EFE=ESC+STFC,E=2+7=9
B→E;EFE=EFB+FTFB,E=4+15=19
从左到右,取两者较大值,所以EFE=19,ESE=19-6=13:
(5)EFD=EFB+FTFB,D=4+10=14,ESD=14-8=6:
(6)D→F;ESF=EFD=14
E→F;ESF=EFE=19
从左到右,取两者较大值,所以ESF=19,EFF=19+0=19:
(7)LAGA,C=ESC=(ESA+STSA,C)=2-(0+2)=0;
(8)LAGA,B=EFB-(ESA+STFA,B)=4-(0+4)=0;
(9)LAGC,E=EFE-(ESC+STFC,E)=19-(2+7)=10:
(10)LAGB,E=EFE-(EFB+FTFB,E)=19-(4+15)=0:
(11)LAGB,D=EFD-(EFB+FTFB,D)=14-(4+10)=0;
(12)LAGD,F=ESF-EFD=19-14=5;
(13)LAGF,F=ESF-EFE=19-19=0:
(14)LAGA,B=LAGB,E=LAGE,F=0;
所以A→B→E→F为关键线路。 -
第5题:
某工程单代号搭接网络计划如下图所示,节点中下方数字为该工作的持续时间,其中关键工作是( )
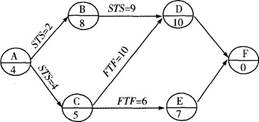 A.工作A
A.工作A
B.工作B
C.工作C
D.工作D
E.工作E答案:A,B,D解析:单代号搭接网络计划可以利用相邻两项工作之间的时间间隔来判定关键线路。即从搭接网络计划的终点节点开始,逆着箭线方向依次找出相邻两项工作之间的时间间隔为零的线路就是关键线路。由图分析可知关键工作为C、E、F。@## -
第6题:
某工程单代号网络计划如下图所示,节点中下方数字为该工作的持续时间,其中的关键工作有()。 A.工作A
A.工作A
B.工作B
C.工作C
D.工作D
E.工作E答案:A,C解析:考核单代号网络计划时间参数的计算。单代号网络计划可以利用相邻两项工作之间的时间间隔来判定关键线路。即从网络计划的终点节点开始,逆着箭线方向依次找出相邻两项工作之间的时间间隔为零的线路就是关键线路。关键线路为A→C→G→I→K和A→C→H→K。参见教材P59。 -
第7题:
某工程单代号搭接网络计划如下图所示,节点中下方数字为该工作的持续时间,其中的关键工作有()。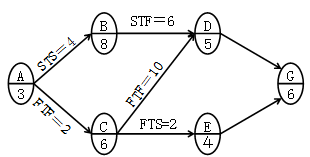 A.工作A和工作D
A.工作A和工作D
B.工作C和工作D
C.工作A和工作E
D.工作C和工作E答案:B解析:考核单代号搭接网络计划。关键线路是A→C→D→G。参见教材P83。 -
第8题:
某分部工程单代号搭接网络计划如图3-50所示,节点中下方数字为该节点所代表工作的持续时间,关键工作是()。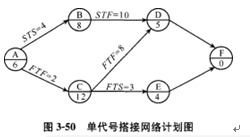 A.工作C和工作D
A.工作C和工作D
B.工作A和工作B
C.工作C和工作E
D.工作B和工作D答案:A解析:2020教材P79-83
本题考查的是单代号搭接网络计划。从图中的A工作和C工作搭接关系KTF=2可以推断出A工作不是起始工作,需要在单代号网络图中增加一个起始工作S作为起始节点。依据各项的搭接关系和持续时间可以得到该网络图中C工作和D工作是关键工作。 -
第9题:
某工程单代号搭接网络计划如下图所示,节点中下方数字为该工作的持续时间,其中关键工作有( ) 。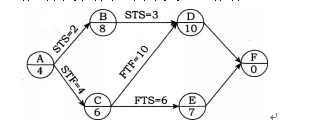
A.工作A
B.工作B
C.工作C
D.工作D
E.工作E答案:C,E解析:本题考查的是单代号搭接网络计划。单代号搭接网络计划可以利用相邻两项工作之间的时间间隔来判定关键线路。即从搭接网络计划的终点节点开始,逆着箭线方向依次找出相邻两项工作之间的时间间隔为零的线路就是关键线路。关键线路为C—E—F。 -
第10题:
某工程单代号搭接网络计划如下图所示,节点中下方数字为该工作的持续时间,其中关键工作是()。 A.工作A和工作B
A.工作A和工作B
B.工作C和工作D
C.工作B和工作E
D.工作C和工作E答案:D解析: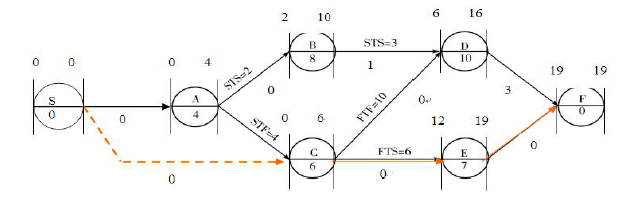
-
第11题:
某工程单代号搭接网络计划如下图所示,节点中下方数字为该工作的持续时间,其中关键工作有( )。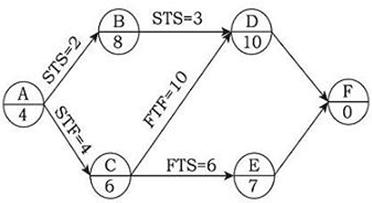 A.工作A
A.工作A
B.工作B
C.工作C
D.工作D
E.工作E答案:C,E解析:本题考查的是搭接网络计划方法。总时差最小的工作为关键工作。从网络的起点到终点均为关键工作,且所有工作的时间间隔均为零的路线为关键路线。考前押题,瑞牛题库软件考前更新,下载链接 www.niutk.com 关键线路为C→E→F。 -
第12题:
多选题某工程单代号搭接网络计划如下图所示,节点中下方数字为该工作的持续时间,其中的关键工作有()。A工作A
B工作B
C工作C
D工作D
E工作E
正确答案: B,C解析: 暂无解析 -
第13题:
某工程单代号搭接网络计划如下图所示,节点中下方数字为工作的持续时间,其中关键工作有( )。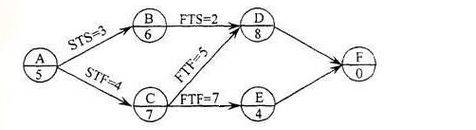
A、工作A
B、工作B
C、工作C
D、工作D
E、工作E答案:A,B,D解析:本题考查的是单代号搭接网络计划。单代号搭接网络计划可以利用相邻两项工作之间的时间间隔来判定关键线路。即从搭接网络计划的终点节点开始,逆着箭线方向依次找出相邻两项工作之间的时间间隔为零的线路就是关键线路。通过时间参数的计算,可以得出关键线路为ABDF。参见教材P83。 -
第14题:
某分部工程单代号网络计划如下图所示,节点中下方数字为该工作的持续时间(单位:天),其关键线路有( )条。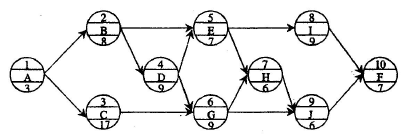 A.1
A.1
B.2
C.3
D.4答案:B解析: -
第15题:
某工程单代号搭接网络计划如下图所示,节点中下方数字为该工作的持续时间,其中的关键工作有()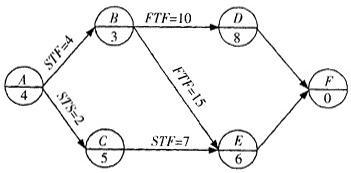 A、工作A
A、工作A
B、工作B
C、工作C
D、工作D
E、工作E答案:A,B,E解析:①ESA=0,EFA=0+4=4。②EFB=ESA+STFA,B=0+4=4,ESB=4-3=1。③ESC=ESA+STSA,C=0+2=2。④C→E:EFE=ESC+STFC,E=2+7=9。B→E:EFE=EFB+FTFB,E=4+15=19。从左到右,取两者较大值,所以EFE=19,ESE=19-6=13。⑤EFD=EFB+FTFB,D=4+10=14。ESD=14-8=6。⑥D→F:ESF=EFD=14。E→F:ESF=EFE=19。从左到右,取两者较大值,ESF=19,EFF=19+0=19。⑦LAGA,C=ESC-(ESA+STSA,C)=2-(0+2)=0。⑧LAGA,B=EFB-(ESA+STFA,B)=4-(0+4)=0。⑨LAGC,E=EFE-(ESC+STFC,E)=19-(2+7)=10。⑩LAGB,E=EFE-(EFB+FTFB,E)=19-(4+15)=0。(11)LAGB,D-EFD-(EFB+FTFB,D)=14-(4+10)=0。(12)LAGD,F=ESF-EFD=19-14=5。(13)LAGE,F=ESF-EFE=19-19=0。(14)LAGA,B=LAGB,E=LAGE,F=0。所以A、B、E、F为关键线路。 -
第16题:
某工程单代号连接网络计划如下图所示,节点中下方数字为工作的持续时间,其中关键工作有()。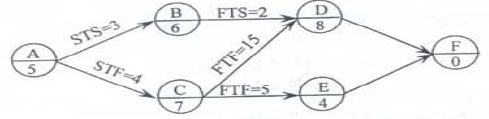 A.工作A和工作B
A.工作A和工作B
B.工作B和工作D
C.工作C和工作D
D.工作C和工作E答案:C解析: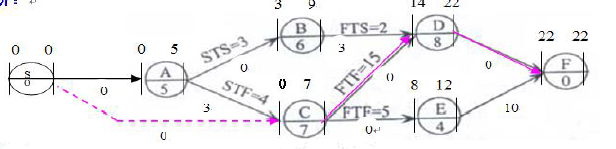
-
第17题:
某工程单代号搭接网络计划如下图所示,节点中下方数字为该工作的持续时间,其中的关键工作有()。
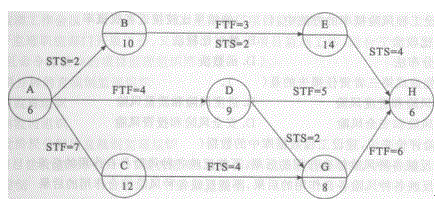 A.工作A.B.E
A.工作A.B.E
B.工作A.C.G
C.工作B.E.H
D.工作C.G、H答案:A解析:首先计算各项工作最早时间,再计算相邻工作之间的时间间隔,即可找出关键线路。@##
-
第18题:
某工程单代号搭接网络计划如下图所示,节点中下方数字为该工作的持续时间,其中的关键工作为( )。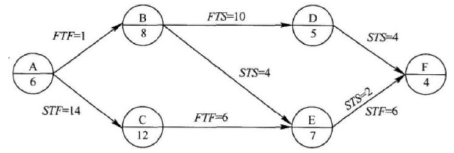 A.工作A、工作C 和工作E
A.工作A、工作C 和工作E
B.工作B、工作D 和工作F
C.工作C、工作E 和工作F
D.工作B、工作E 和工作F答案:B解析:本题考核的是单代号搭接网络计划中关键工作的确定。本题中工作A 的最早开始时间就等于零,即:ESA=0,EFA=6。其他工作的最早开始时间和最早完成时间计算如下。
-
第19题:
某工程单代号搭接网络计划如图3-16所示,节点中下方数字为该工作的持续时间,其中的关键工作有()。 A.工作A
A.工作A
B.工作B
C.工作C
D.工作D
E.工作E答案:B,E解析:2020教材P79-83
本题考查的是关键工作的确定。第一步根据已知条件,算出各工作的最早开始时间和最早完成时间;第二步计算相邻两项工作之间的时间间隔;第三步利用相邻两项工作之间的时间间隔来判定关键线路。关键线路上的工作即为关键工作。从单代号搭接网络计划的终点节点开始,逆着箭头方向依次找出相邻两项工作之间时间间隔为零的线路即为关键线路。关键线路上的工作即为关键工作。本题中,先计算出各工作的最早开始时间和最迟开始时间,如图3-17所示。
第一步:各工作的最早开始时间和最早完成时间为如下所述:
工作A:ESA=0,EFA=4。
工作B:根据STF=4,得EFB=4,ESB=-2,显然不合理,为此,应将工作B与虚拟工作S(起点节点)相连,重新计算工作B的最早开始时间和最早完成时间为ESB=0,EFB=6。
工作C:根据STS=2得ESC=2,EFC=12。
工作D:根据STS=8得ESD=8,EFD=15。
工作E:根据FTS=1得ESE=13;根据 FTF=20得EFE=26,ESE=17,取大值, 得EFE=26,ESE=17。
工作G:根据STF=10得EFG=18, ESG=12;根据STS=2得ESG=19,EFG=25;取大值即计算工期为25。
由于在搭接网络计划中,决定工期的工作不一定是最后进行的工作。因此,在用上述方法完成计算之后,还应检查网络计划中其他工作的最早完成时间是否超过已计算出的计算工期。经查,工作E的最早完成时间26为最大,故网络计划的计算工期是由工作E的最早完成时间决定的。为此,应将工作E与一个虚拟工作F(终点节点)用虚箭线相连,得到工作F的最早开始时间和最早完成时间为26。
第二步:计算相邻两项工作之间的时间间隔。
计算中由于工作B的最早开始时间出现负值,故应将工作B与虚拟起点节点S用虚箭线相连。另外由于工作E的最早完成时间为最大,故应将工作E与虚拟结束结点F用虚箭线相连(图3-17)。
然后依据相邻两项工作之间的搭接关系的不同,分别计算出相邻两项工作之间的时间间隔LAG,本题中的各相邻两项工作间的时间间隔标注于图3-17中箭线的下方。由图中可知,经计算只有工作B和工作E之间的时间间隔为0,而工作B是和一个虚拟的起始工作S相连,而工作E是和一个虚拟的终点节点相连的,该网络计划的关键线路为S—B—EF,关键工作为工作B和工作E。 -
第20题:
某工程单代号搭接网络计划如下图所示,节点中下方数字为该工作的持续时间,其中关键工作有()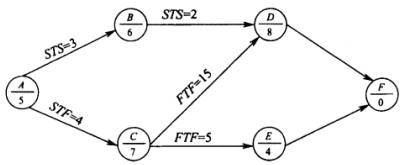 A、工作A和工作B
A、工作A和工作B
B、工作B和工作D
C、工作C和工作D
D、工作C和工作E答案:C解析:首先计算各工作的最早开始时间和最早结束时间,在计算工作C的最早开始时间时出现负值,应增加虚拟的开始节点,将其与工作A和工作C节点用虚箭线相连,重新计算工作A和工作C的时间参数;再计算相邻工作之间的时间间隔,最后从结束节点返回,无时间间隔的就画,所连接的线路A-C-D-F就是关键线路,C、D两项工作为关键工作,故选C项。 -
第21题:
某工程单代号搭接网络计划如下图所示,其中关键工作有()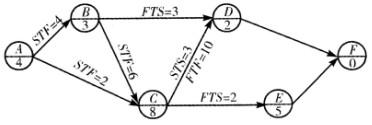 A、工作A和工作答案:A解析:在单代号搭接网络中,可以利用相邻两项工作间的时间间隔来判定关键线路。即从搭接网络计划的终点节点开始,逆着箭线方向依次找出相邻两项工作之间时间间隔为零的线路就是关键线路。关键线路上的工作即为关键工作。
A、工作A和工作答案:A解析:在单代号搭接网络中,可以利用相邻两项工作间的时间间隔来判定关键线路。即从搭接网络计划的终点节点开始,逆着箭线方向依次找出相邻两项工作之间时间间隔为零的线路就是关键线路。关键线路上的工作即为关键工作。 -
第22题:
某分部工程单代号搭接网络计划如下图所示,节点中下方数字为该节点所代表工作的持续时间,关键工作是()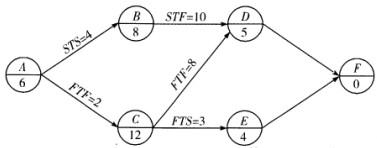 A、工作C和工作D
A、工作C和工作D
B、工作A和工作B
C、工作C和工作E
D、工作B和工作D答案:A解析:总时差最小的工作为关键工作。由图可知,此网络图的工期为23天,其中关键工作有:C、D、F。 -
第23题:
某工程项目的单代号网络计划如下图所示。图中节点下方的数字为该工作的持续时间(单位:月)。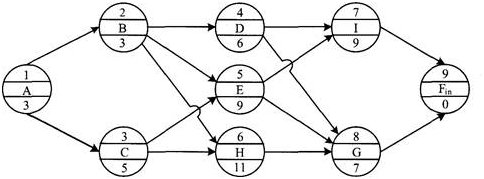
该工程项目进度计划的关键线路为( )。A.①—②—④—⑦—⑨
B.④—③—⑤—⑦—⑨
C.①—②—⑥—⑧—⑨
D.①—③—⑥—⑧—⑨答案:B,D解析:此题考查网络图的线路。网络图中从起点节点开始,沿箭头方向顺序通过一系列箭线与节点,最后达到终点节点的通路称为线路。线路上各项工作持续时间的总和称为该线路的计算工期。一般网络图有多条线路,可依次用该线路上的节点代号来记述,其中最长的一条线路称为关键线路,位于关键线路上的工作称为关键工作。本题中,①—③—⑥—⑧—⑨为一条关键线路,①—③—⑤—⑦—⑨为另一条关键线路,时间都为26个月。@##
