如下图所示,A、B、C、D为一块梯形田地的4个顶点。已知BC比AD长16米,三角形ACD面积比ABC小200平方米。问AD到BC的距离是多少米?A.12.5 B.18.5 C.20 D.25
题目
如下图所示,A、B、C、D为一块梯形田地的4个顶点。已知BC比AD长16米,三角形ACD面积比ABC小200平方米。问AD到BC的距离是多少米?
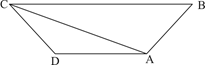

A.12.5
B.18.5
C.20
D.25
B.18.5
C.20
D.25
相似考题
更多“如下图所示,A、B、C、D为一块梯形田地的4个顶点。已知BC比AD长16米,三角形ACD面积比ABC小200平方米。问AD到BC的距离是多少米? ”相关问题
-
第1题:
将一块三角形绿地沿一条直线分成两个区域,一块为三角形,一块为梯形,已知分出的三角行区域的面积为1.2亩,梯形区域的上、下底边分别为80米、240米,问分出的梯形区域的面积为多少亩? ( )
A.9.6
B.11.2
C.10.8
D.12.0
正确答案:A
39.A【解析】如图,因为梯形区域的上、下底边分别为80米、240米,所以分出的三角形区域的面积和整个大三角形面积比就是1:9,分出的三角行区域的面积和分出的梯形区域的面积比就是1:8,所以分出的梯形区域的面积为1.2×8=9.6亩。 -
第2题:
△ABC是直角三角形,阴影Ⅰ的面积比阴影Ⅱ的面积小25平方厘米,AB长度为8厘米,则BC的长度约是( )厘米。(π=3.14)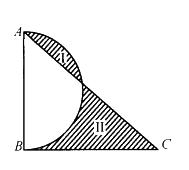 A. 12. 47
A. 12. 47
B. 20. 47
C. 12.53
D. 17.33答案:C解析:已知阴影Ⅱ减去阴影Ⅰ等于25平方厘米,则△ABC的面积减去半圆的面积也等于25平方厘米,故△ ABC的面积为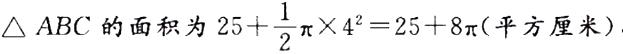 ,BC =(25 +8π) X2 ÷ 8 = 6. 25 + 2π=12. 53(厘米)。
,BC =(25 +8π) X2 ÷ 8 = 6. 25 + 2π=12. 53(厘米)。 -
第3题:
如图,已知一个四边形中边AD长为3cm,边BC长7cm;∠DAB=135°,∠ABC=∠ADC=90°那么这个四边形的面积是( )cm2。
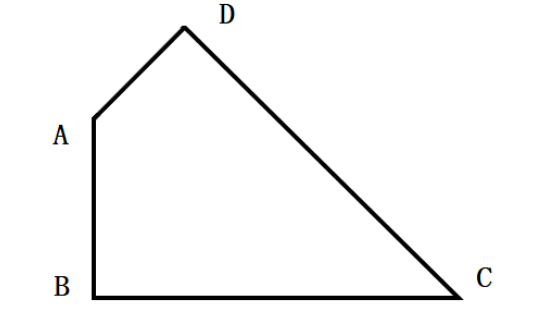
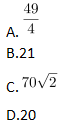 答案:D解析:第一步,本题考查几何问题,用割补平移法解题。
答案:D解析:第一步,本题考查几何问题,用割补平移法解题。
第二步,作BA和CD的延长线交于E,如图所示,得到三角形EBC和ADE。容易知道所求四边形ABCD面积等于△EBC面积减去△ADE面积。由题意∠DAB=135°,∠ABC=∠ADC=90°,可以求得∠DCB=360°-135°-90°×2=45°,且∠BEC=∠EAD=45°,所以△EBC和△ADE都是等腰直角三角形。
第三步,因为AD长3cm,BC长7cm,则BE=BC=7cm,DE=AD=3cm,所以
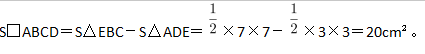
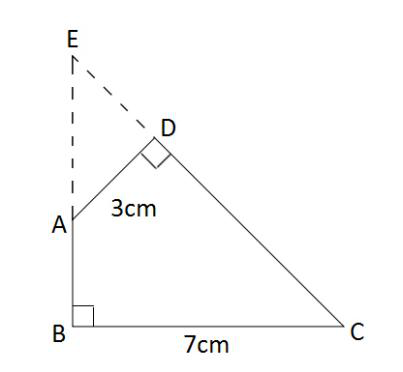
-
第4题:
如图所示,半圆与等腰三角形ABC的斜边AC相切,AB=BC=1。问半圆的直径是多少?
A. 根号2减1
B. 1比根号2
C. 2乘根号2减2
D. 3减2乘根号2答案:C解析: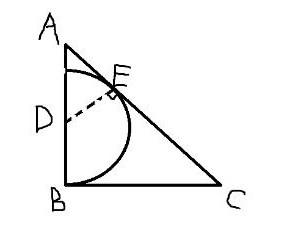
设:圆心为点D,半圆与△ABC的斜边的切点为点E,连接DE 由“圆心和切点的连线垂直于切线”可知DE⊥AC 即∠AED=90° 由AB=BC=1 得此三角形为等腰直角三角形即 ∠BAC=∠BCA=45° 所以∠ADE=45° 即△ADE为等腰直角三角形 AE=DE 设 DE=x 则 BD=DE=AE=x AD=√2x 所以 AB=AD+DB=√2x+x=1 解之得 x=√2-1 即DE=√2-1 因此 半圆的直径 d=2(√2-1)=2√2-2 -
第5题:
如图所示,△ABC中DE∥BC,且BO和CO分别是∠ABC和∠ACB的角平分线。已知AB=25.4 cm,BC=24.5 cm,AC=20 cm。问△ADE的周长是多少?
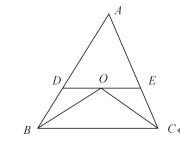
A.45.4 cm B.45.1 cm C.44.8 cm D.44.5 cm答案:A解析:根据题意可知,DO=BD,OE=EC,则△ADE的周长=AB+AC=45.4 cm。 -
第6题:
如右图所示,梯形ABCD的对角线AC⊥BD,其中AD=1/2,BC=3,AC=14/5 ,BD=2.1.问梯形ABCD的高AE的值是: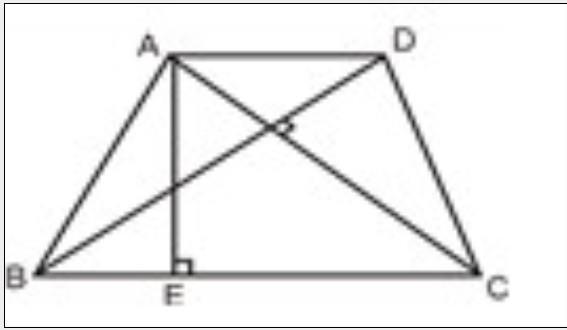
A. 43/24
B. 1.72
C. 42/25
D. 1.81答案:C解析:解题指导: C。 -
第7题:
如图所示,梯形ABCD,AD//BC,DE丄BC,现在假设AD、BC的长度 ’都减少10%,DE的长度增加10%,则新梯形的面积与原梯形的面积相比,会( )。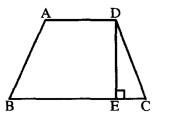
A.不变 B.减少1% B-ECC.增加10% D.减少10%答案:B解析:梯形 ABCD 的面积= (AD+BC)XDE/2;AD、BC的长度都减少10%,DE的长度增加10%,则梯形ABCD的面积=(1 一 10%) X (AD+BC) X (1 +10 %) X DE/2 = 99 % X ( AD+BC) X DE/2。 新梯形的面积与原梯形的面积相比,减少1%。 -
第8题:
如图,已知一个四边形中边AD长为3cm,边BC长7cm;∠DAB=135°,∠ABC=∠ADC=90°那么这个四边形的面积是( )。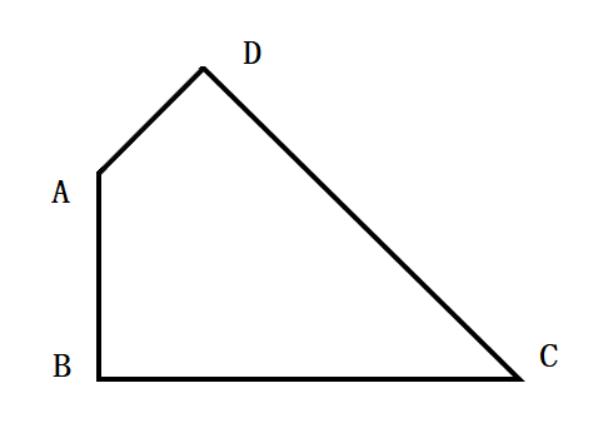
A.49/4
B.21
C.
D.20答案:D解析:
-
第9题:
下图为以AC、AD和AF为直径画成的三个圆形,已知AB、BC、CD、DE和EF之间的距离彼此相等。问小圆x、弯月y以及弯月z三部分的面积之比为: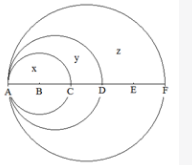 A.4:5:16
A.4:5:16
B.4:5:14
C.4:7:12
D.4:3:10答案:A解析:第一步,本题考查几何问题,属于平面几何类。
第二步,赋值AB=2,由AB、BC、CD、DE、EF之间的距离相等,可得AC=4、AD=6、AF=10。则小圆、中圆、大圆的半径分别为2、3、5。
第三步,小圆x、弯月y以及弯月z的面积分别为4π、9π-4π=5π、25π-9π=16π,故三部分的面积之比为4∶5∶16。 -
第10题:
如图6-9所示,在△ABC中,AD⊥BC于D点,BD=CD,若BC=6,AD=5,则图中阴影部分的面积为( )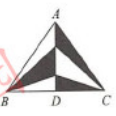 A.3
A.3
B.7.5
C.15
D.30
E.5.5答案:B解析:
-
第11题:
如右图所示,梯形ABCD的对角线AC丄BD,其中AD=1/2,BC=3,AC=2,BD=2.1,则梯形ABCD的髙AE的值是()。
 答案:C解析:由ACXBD=(AD+BC)XAE=>AE=42/45。
答案:C解析:由ACXBD=(AD+BC)XAE=>AE=42/45。 -
第12题:
已知Rt△ABC中,斜边BC上的高AD=4,cosB=4/5,则AC=5。
正确答案:正确 -
第13题:
一块三角形农田ABC(如下图所示)被DE、EF两条道路分为三块。已知BD=2AD,CE=2AE,CF=2BF,则三角形ADE、三角形CEF和四边形BDEF的面积之比为: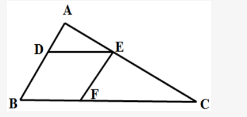 A.1∶3∶3
A.1∶3∶3
B.1∶3∶4
C.1∶4∶4
D.1∶4∶5答案:C解析:解法一:
第一步,本题考查几何问题,属于平面几何类,用比例法解题。
第二步,由BD=2AD,CE=2AE,CF=2BF,则DE∥BC,EF∥AB,即四边形BDEF是平行四边形,可得BD=EF,DE=BF。△ADE与△EFC与△ABC相似,所以边长比的平方等于面积比,所以
因此三角形ADE与四边形BDEF的面积比为1∶4,所以三者比值为1∶4∶4。
因此,选择C选项。
解法二:
第一步,本题考查几何问题,属于平面几何类,用代入排除法解题。
第二步,由题意知,△ADE与△ABC相似,且AD∶AB=1∶3,根据几何比例关系,=1∶9。代入A选项,1∶(1+3+3)=1∶7≠1∶9,排除;代入B选项,1∶(1+3+4)=1∶8≠1∶9,排除;代入C选项,1∶(1+4+4)=1∶9,满足;代入D选项,1∶(1+4+5)=1∶10≠1∶9,排除。 -
第14题:
如图.已知圆⊙O是△ABC的外接圆,AD是圆⊙0的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB。
(1)求证:BE是⊙0的切线;
(2)若BC=√3,AC=5,求圆的直径AD及切线BE的长。答案:解析:(1)连接OB,∵AD是圆⊙O的直径'∴∠OBD+∠EBD=90°, ∵BD=BC,∴其劣弧所对的圆周角相等,即∠CAB=∠BAD,
∵AO=BO,∴∠BAD=∠ABO,
又∠EBD=∠CAB,∴∠EBD=ABO,∴∠OBD+∠ABO=90°,∴∠OBE=90°,
∵B0是圆的半径,∴BE是⊙O的切线。
(2)设圆的半径为r,连接CD交OB于F,
设圆的半径为R,连接CD,.
-
第15题:
下图中阴影1的面积比阴影2的面积多28平方厘米,AB=40cm,BC垂直于AB,求BC 的长。(π 取 3.14)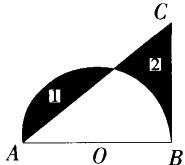 A.20cm
A.20cm
B.25cm
C.30cm
D.35cm答案:C解析: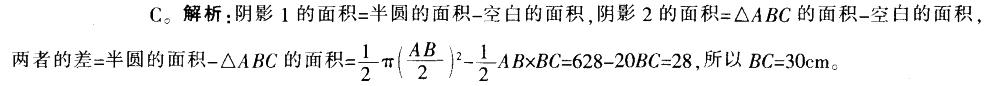
-
第16题:
如下图所示,A、B、C、D为一块梯形田地的4个顶点。已知BC比AD长16米,三角形ACD面积比ABC小200平方米。问AD到BC的距离是多少米?
 A.12.5
A.12.5
B.18.5
C.20
D.25答案:D解析:第一步,本题考查几何问题,属于平面几何类。
第二步,设AD为x,AD距离BC为h,根据题意得
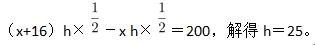
-
第17题:
如图所示,梯形ABCD,AD∥BC,DE⊥BC,现在假设AD、BC的长度都减少10%,DE的长度增加10%,则新梯形的面积与原梯形的面积相比,会怎样变化?
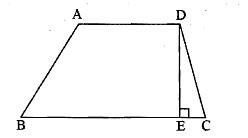
A. 不变
B. 减少1%
C. 增加10%
D. 减少10%答案:B解析:解题指导: S=90%(AD+BC)*100%DE÷2=99(AD+BC)*DE÷2,所以减少了1%。故答案为B。 -
第18题:
如图所示,梯形ABCD的两条对角线AD、BC相交于O,EF平行于两条边且过O点。现已知AB=6,CD=18。问EF的长度为多少?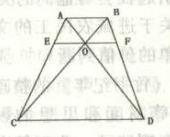 A. 8.5
A. 8.5
B. 9
C. 9.5
D. 10答案:B解析:解题指导: 18*BF/BD=6*DF/BD, BF/DF=1:3, OF/CD=1:4, OE/CD=1:4, EF=CD/2=9,故答案为B。 -
第19题:
如下图所示,已知△ABC的面积为240平方厘米,D是BC的中点,AD的长是AE长的3倍,EF的长是BF长的3倍,那么,△AEF的面积是多少平方厘米?( )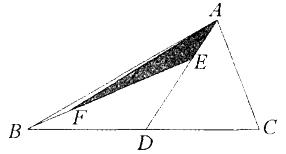 A. 27.5
A. 27.5
B. 40
C. 30
D. 25答案:C解析:若已知两个三角形的高相等,则二者面积之比等于底边之比。本题中D是BC的中点,故
-
第20题:
人行道ABC,BC长286cm,D为BC中点。AD直线距离为324cm,过B点做直线BE,过C点做垂线与BE交于E点,问AE最小距离为多少? A.38cm
A.38cm
B.168cm
C.176cm
D.181cm答案:D解析:第一步,本题考查几何问题,属于平面几何类。
第二步,如图所示,E点的轨迹应该是一个以BC为直径、D为圆心的半圆。最短的距离为AD连线交圆于E点的AE,此距离为324-ED。在直角三角形BEC中DE是斜边的中线,距离是斜边的一半即286÷2=143cm,则最短距离为324-143=181cm。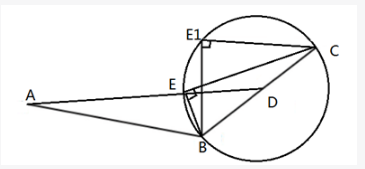
-
第21题:
在三角形ABC,AB=4,AC=6,BC=8,D为BC的中点,则AD=
 答案:B解析:
答案:B解析:
-
第22题:
如,在直角三角形ABC中,AC=4,BC=3,DE//BC,已知梯形BCDE的面积为3,则DE长为( )
 答案:D解析:
答案:D解析:
-
第23题:
如图,等腰梯形ABCD中,AD∥BC,AD=5,AB=6,BC=8, AB∥DE,求△DEC的周长。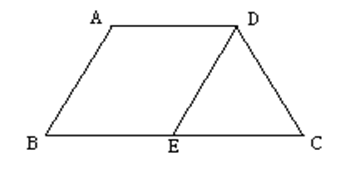 答案:解析:15
答案:解析:15 -
第24题:
判断题已知Rt△ABC中,斜边BC上的高AD=4,cosB=4/5,则AC=5。A对
B错
正确答案: 对解析: 暂无解析
