阅读下列函数说明和C函数,将应填入(n)处的字句写在对应栏内。[说明]邻接表是图的一种顺序存储与链式存储结合的存储方法。其思想是:对于图G中的每个顶点 vi,将所有邻接于vi的顶点vj连成一个单链表,这个单链表就称为顶点vi的邻接表,其中表头称作顶点表结点VertexNode,其余结点称作边表结点EdgeNode。将所有的顶点表结点放到数组中,就构成了图的邻接表AdjList。邻接表表示的形式描述如下: define MaxVerNum 100 /*最大顶点数为100*/typedef struct no
题目
阅读下列函数说明和C函数,将应填入(n)处的字句写在对应栏内。[说明]
邻接表是图的一种顺序存储与链式存储结合的存储方法。其思想是:对于图G中的每个顶点 vi,将所有邻接于vi的顶点vj连成一个单链表,这个单链表就称为顶点vi的邻接表,其中表头称作顶点表结点VertexNode,其余结点称作边表结点EdgeNode。将所有的顶点表结点放到数组中,就构成了图的邻接表AdjList。邻接表表示的形式描述如下: define MaxVerNum 100 /*最大顶点数为100*/
typedef struct node{ /*边表结点*/
int adjvex; /*邻接点域*/
struct node *next; /*指向下一个边表结点的指针域*/ }EdgeNode;
typedef struct vnode{ /*顶点表结点*/
int vertex; /*顶点域*/
EdgeNode *firstedge; /*边表头指针*/
}VertexNode;
typedef VertexNode AdjList[MaxVerNum]; /*AdjList是邻接表类型*/
typedef struct{
AdjList adjlist; /*邻接表*/
int n; /*顶点数*/
}ALGraph; /*ALGraph是以邻接表方式存储的图类型*/
深度优先搜索遍历类似于树的先根遍历,是树的先根遍历的推广。
下面的函数利用递归算法,对以邻接表形式存储的图进行深度优先搜索:设初始状态是图中所有顶点未曾被访问,算法从某顶点v出发,访问此顶点,然后依次从v的邻接点出发进行搜索,直至所有与v相连的顶点都被访问;若图中尚有顶点未被访问,则选取这样的一个点作起始点,重复上述过程,直至对图的搜索完成。程序中的整型数组visited[]的作用是标记顶点i是否已被访问。
[函数]
void DFSTraverseAL(ALGraph *G)/*深度优先搜索以邻接表存储的图G*/
{ int i;
for(i=0;i<(1);i++) visited[i]=0;
for(i=0;i<(1);i++)if((2)) DFSAL(G,i);
}
void DFSAL(ALGraph *G,int i) /*从Vi出发对邻接表存储的图G进行搜索*/
{ EdgeNode *p;
(3);
p=(4);
while(p!=NULL) /*依次搜索Vi的邻接点Vj*/
{ if(! visited[(5)]) DFSAL(G,(5));
p=p->next; /*找Vi的下一个邻接点*/
}
}
相似考题
参考答案和解析
(1) G->n (2) ! visited[i] (3) visited[i]=1 (4) G->adjlist[i].firstedge (5) p->adjvex 解析:(1)此处循环是访问标志向量的初始化,应遍历 G的全体点,共计G→n个;
(2)若Vi未被访问,则从Vi开始搜索;
(3)标记Vi已访问;
(4)为递归搜索Vi的邻接点,需先取出Vi边表的头指针;
(5)若Vi的邻接点p->adjvex尚未被访问,则从它出发进行纵深搜索。
更多“阅读下列函数说明和C函数,将应填入(n)处的字句写在对应栏内。[说明] 邻接表是图的一种顺序存储与 ”相关问题
-
第1题:
阅读以下函数说明和C语言函数,将应填入(n)处的字句写在答题纸的对应栏内。
【函数2.1说明】
递归函数sum(int a[], int n)的返回值是数组a[]的前n个元素之和。
【函数2.1】
int sum (int a[],int n)
{
if(n>0) return (1);
else (2);
}
【函数2.2说明】
有3个整数,设计函数compare(int a,int b,int c)求其中最大的数。
【函数2.2】
int compare (int a, int b, int c )
{ int temp, max;
(3) a:b;
(4) temp:c;
}
【函数2.3说明】
递归函数dec(int a[],int n)判断数组a[]的前n个元素是否是不递增的。不递增返回 1,否则返回0。
【函数2.3】
int dec( int a[], int n )
{
if(n<=1) return 1;
if(a[0]<a[1]) return 0;
return (5);
}
正确答案:(1)a[n-1]+sum(an-1)或者a[0]+sum(a+1n-1); (2)return 0; (3)temp=(a>b)? (4)max=(temp>c)? (5)dec(a+1n-1);
(1)a[n-1]+sum(a,n-1)或者a[0]+sum(a+1,n-1); (2)return 0; (3)temp=(a>b)? (4)max=(temp>c)? (5)dec(a+1,n-1); 解析:本题考查C语言函数和一些基本运算。
下面我们分别来分析这几个函数。在函数2.1中,题目要求用此递归函数求数组前 n个元素之和。递归函数的特点是在函数体中不停地调用函数本身,只是将其函数的参数范围改变。题目中要求我们求数组前n个元素之和,我们可以这样理解,即前n个元素之和等于第n个元素加上前n-1个元素之和,现在的问题转化成如何求前n-1个元素之和。同样的道理,可以将求前n-1个元素之和转化成求前n-2个元素之和,直到这个数小于0。从函数2.1的代码中可以知道,在计算以前,首先判断n与0的关系,如果n小于0,说明数组中无元素,因此,返回0值;如果n大于等于0,说明数组中有元素,应该返回的结果是第n个元素加上前n-1个元素之和,而前n-1个元素之和是调用函数本身来计算的。因此,第(1)空和第(2)空的答案分别是a[n-1)+sum(a,n-1),return()。
在函数2.2中,题目要求我们在三个数中取最大数,在数学中,我们从三个数中取最大数时,一般是首先拿其中两个数比较,取较大的数再与第三个数比较,再取其较大的数,这个数就是三个数中的最大数。从函数2.2的代码中知道,三个数a、b、c,两个整型变量temp与max。根据求三个数中最大数的数学过程和函数中已给出的代码可知,第(3)空处语句应该为temp=(a>b)?a:b,求得a、b中较大数并存放在变量temp中。第(4)空处语句为max=(temp>c)?temp:c。
在函数2.3中,题目要求判断数组a[]的前n个元素是否是不递增的。不递增返回1,否则返回0。要判断前n个元素是否是不递增的,需要判断前n-1个元素是否是不递增的,以及第n个元素与第n-1个元素的关系。此处与函数2.1一样,用的都是递归函数,只是出口不同,在函数2.1中,只要数组中没有元素了,递归结束,这里只要第n个元素大于第n-1个元素,则返回0,递归结束。又由if(a[0]a[1])语句可知,在每次调用函数时,都将其数组中的第一个元素与第二个元素比较来作为递归的出口,如果结果为假,就说明数组的前面两项的关系是不递增的,在下次调用中不用再考虑第一项。因此第(5)空应该是dec(a+1,n-1)。 -
第2题:
●试题二
阅读下列函数说明和C代码,将应填入(n)处的字句写在答题纸的对应栏内。
【说明】
该程序运行后,输出下面的数字金字塔

【程序】
include<stdio.h>
main ()
{char max,next;
int i;
for(max=′1′;max<=′9′;max++)
{for(i=1;i<=20- (1) ;++i)
printf(" ");
for(next= (2) ;next<= (3) ;next++)
printf("%c",next);
for(next= (4) ;next>= (5) ;next--)
printf("%c",next);
printf("\n");
}
}
正确答案:
●试题二【答案】(1)(max-′0′)(2)′1′(3)max(4)max-1(5)′1′【解析】该程序共有9行输出,即循环控制变量max的值是从1~9。每行输出分3部分,先用循环for语句输出左边空白,(1)空填"(max-′0′)";再用循环输出从1到max-′0′的显示数字,即(2)空和(3)空分别填1和max;最后输出从max-′1′~1的显示数字,即(4)空和(5)空分别填和max-1和′1′。 -
第3题:
阅读下列说明和C++-代码,将应填入(n)处的字句写在答题纸的对应栏内。 【说明】 某发票(lnvoice)由抬头(Head)部分、正文部分和脚注(Foot)部分构成。现采用装饰(Decorator)模式实现打印发票的功能,得到如图5-1所示的类图。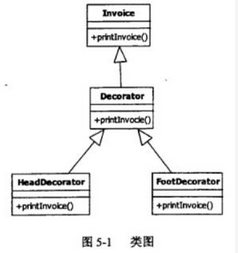
【C++代码】 #includeusing namespace std; class invoice{ public: (1){ cout<<"This is the content of the invoice!"< 答案:解析:(1) virtual void printInvoice() (2) ticket->printInvoice() (3) Decorator::printInvoice() (4) Decorator::printInvoice() (5) &a
【解析】
试题分析
1.Invoice类下,义虛函数,按类图,函数名是printInvoice
2.前面定义对象名是ticket,那么在ticket不为空的时候调用函数printInvoice
3.这部分填写发票的抬头,看类图应该实现函数printInvoice ,Decorator装饰模式使用该方法
4.这部分是发票的脚注,看类图应该实现函数printlnvoice,Decorator装饰模式使用该方法
5.FootDecorator a(NULL) ;脚步的装饰参数是a,调用a参数,第4题:
阅读以下函数说明和C语言函数,将应填入(n)处的字句写在对应栏内。
[说明]
已知r[1...n]是n个记录的递增有序表,用折半查找法查找关键字为k的记录。若查找失败,则输出“failure",函数返回值为0;否则输出“success”,函数返回值为该记录的序号值。
[C函数]
int binary search(struct recordtype r[],int n,keytype k)
{ intmid,low=1,hig=n;
while(low<=hig){
mid=(1);
if(k<r[mid].key) (2);
else if(k==r[mid].key){
printf("succesS\n");
(3);
}
else (4);
}
printf("failure\n");
(5);
}
正确答案:(1) (low+hig)/2 (2) hig=mid-1 (3) returnmid (4) low=mid+1 (5) return 0
(1) (low+hig)/2 (2) hig=mid-1 (3) returnmid (4) low=mid+1 (5) return 0 解析:折半查找法也就是二分法:初始查找区间的下界为1,上界为len,查找区间的中界为k=(下界+上界)/2。所以(1)应填“(low+hig)/2”。中界对应的元素与要查找的关键字比较。当kr[mid].key时,(2)填“hig=mid-1”;当k==r[mid].key时,(3)填“return mid”;当k>r[mid].key时,(4)填“low=mid+1”。如果low>hig时循环终止时,仍未找到需查找的关键字,那么根据题意返回0,即空(5)填“return 0”。第5题:
试题三(共 15 分)
阅读以下说明和 C 程序,将应填入 (n) 处的字句写在答题纸的对应栏内。
 正确答案:
正确答案:
第6题:
阅读下列说明和?C++代码,将应填入(n)处的字句写在答题纸的对应栏内。
【说明】
阅读下列说明和?Java代码,将应填入?(n)?处的字句写在答题纸的对应栏内。
【说明】
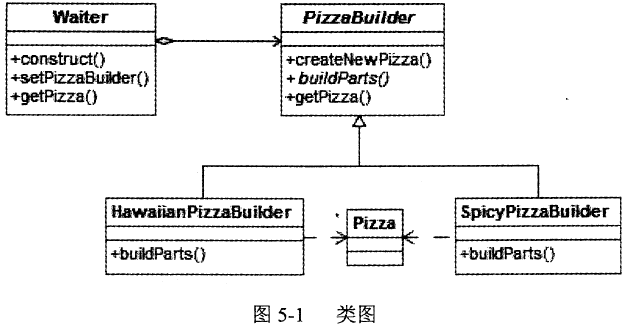
某快餐厅主要制作并出售儿童套餐,一般包括主餐(各类比萨)、饮料和玩具,其餐品种
类可能不同,但其制作过程相同。前台服务员?(Waiter)?调度厨师制作套餐。现采用生成器?(Builder)?模式实现制作过程,得到如图?6-1?所示的类图。


 答案:解析:
答案:解析:
