某商品的销售量对于进货量的百分比与销售价格成反比例,已知销售单价为8元时,可售出进货量的 80%。又销售价格与进货价格成正比例,已知进货价格为5元时,销售价格为8元,在以上的比例系数不变的情况下,当进货价格为6元时,可售出进货量的百分比为(28)。A.67%B.74%C.76%D.78%
题目
某商品的销售量对于进货量的百分比与销售价格成反比例,已知销售单价为8元时,可售出进货量的 80%。又销售价格与进货价格成正比例,已知进货价格为5元时,销售价格为8元,在以上的比例系数不变的情况下,当进货价格为6元时,可售出进货量的百分比为(28)。
A.67%
B.74%
C.76%
D.78%
相似考题
参考答案和解析
正确答案:A
解析:设该商品的销售量相对于进货量的百分比为A,销售价格为B,进货价格为C。依题意得,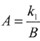 ,B=k2C,其中,k1、k2,为比例系数。
,B=k2C,其中,k1、k2,为比例系数。
又由80%=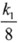 ,8=5k2,求得k1=6.4,k2=1.6,故
,8=5k2,求得k1=6.4,k2=1.6,故 ,B=1.6C。
,B=1.6C。
当C=6时,B=1.6×6=9.6, ,故正确答案为A。
,故正确答案为A。
解析:设该商品的销售量相对于进货量的百分比为A,销售价格为B,进货价格为C。依题意得,
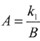 ,B=k2C,其中,k1、k2,为比例系数。
,B=k2C,其中,k1、k2,为比例系数。又由80%=
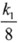 ,8=5k2,求得k1=6.4,k2=1.6,故
,8=5k2,求得k1=6.4,k2=1.6,故 ,B=1.6C。
,B=1.6C。当C=6时,B=1.6×6=9.6,
 ,故正确答案为A。
,故正确答案为A。
更多“某商品的销售量对于进货量的百分比与销售价格成反比例,已知销售单价为8元时,可售出进货量的 80%。 ”相关问题
-
第1题:
将进货单价为90元的某商品按100元一个出售时,能卖出500个,已知这种商品如果每个涨价1元,其销售量就会减少10个,为了获得最大利润,售价应定为:
A. 110元
B. 120元
C. 130元
D. 150元答案:B解析:解题指导: 假设为了获得最大利润,需要在售价100元的基础上再涨价x元,这时候的销售数量在500个的基础上减少的是y个,总利润是M元,则有:总利润=单个利润×出售的个数,M=(100-90+x)×(500-y)=(10+x)×(500-y)= 5000-10y+500x-xy (1)又:题目上说“商品如果涨1元,出售数量就少10个”,也就是x等于1的时候,y等于10;x等于2的时候,y等于20,所以有: y=10x (2) 把式子(2)代入式子(1)得: M=-10x^2+400x+5000 这是一个开口向下的抛物线,其中:a=-10,b=400,c=5000,要想M取得最大值, x=-b/2a=-400÷[2×(-10)]=20, 即在售价100元的基础上再涨价20元,也就是售价120元,这时候的最大利润就是9000元。故答案为B。 -
第2题:
将进货单价为90元的某商品按100元一个出售时,能卖出500个,已知这种商品如果每个涨价1元,其销售量就会减多10个,为了获得最大利润,售价应定为( )
A.110元 B.120元 C.130元 D.150元答案:B解析:
-
第3题:
(本题满分10分)设有某商品的需求量r分布如下表: r 400 500 600 700 800 900 P(r) 0.05 0.10 0.25 0.35 0.15 0.10 已知该商品的购进单价为15元,出售单价为18元,若当天未能售出,第二天的处理价格为11元,这时一定可售完,试求合理的进货数量。
AD -
第4题:
将进货单价为90元的某商品按100元一个出售时,能卖出500个,已知这种商品如果每个涨价1元,其销售量就会减少10个,为了获得最大利润,售价应定为:( )。
A.110元
B.130元
C.120元
D.150元答案:C解析:设涨价x元,此时利润为y,则y=(100+x-90)×(500-10×x),该函数为二次函数,其最值可使用导数求得。当x=20时,利润最大。故正确答案为C。 -
第5题:
某商品的进货单价为80元,销售单价为100元,每天可售出120件。已知销售单价每降低1元,每天可多售出20件。若要实现该商品的销售利润最大化,则销售单价应降低的金额是()《》A.5元
B.6元
C.7元
D.8元答案:C解析:
