itgle.com
阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏内。 【说明】 下面流程图的功能是:在给定的一个整数序列中查找最长的连续递增子序列。设序列存放在数组 A[1:n](n≥2)中，要求寻找最长递增子序列 A[K: K+L-1] (即A[K]<A[K+1]<…<A[K+L-1])。流程图中，用 Kj 和Lj 分别表示动态子序列的起始下标和长度，最后输出最长递增子序列的起始下标 K 和长度 L。 例如，对于序列 A={1 ，2，4，4 ，5，6，8，9，4，5，8}，将输出K
题目
阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏内。 【说明】 下面流程图的功能是:在给定的一个整数序列中查找最长的连续递增子序列。设序列存放在数组 A[1:n](n≥2)中，要求寻找最长递增子序列 A[K: K+L-1] (即A[K]<A[K+1]<…<A[K+L-1])。流程图中，用 Kj 和Lj 分别表示动态子序列的起始下标和长度，最后输出最长递增子序列的起始下标 K 和长度 L。 例如，对于序列 A={1 ，2，4，4 ，5，6，8，9，4，5，8}，将输出K=4， L=5。
【流程图】
注:循环开始框内应给出循环控制变量的初值和终值，默认递增值为1，格式为: 循环控制变量=初值，终值
相似考题
更多“阅读以下说明和流程图,填补流程图中的空缺,将解答填入答题纸的对应栏内。 【说明】 下面流程图的 ”相关问题
-
第1题：
阅读以下说明和流程图，填补流程图中的空缺(1)～(9)，将解答填入对应栏内。
【说明】
假设数组A中的各元素A(1)，A(2)，…，A(M)已经按从小到大排序(M≥1)；数组B中的各元素B(1)，B(2)，…，B(N)也已经按从小到大排序(N≥1)。执行下面的流程图后，可以将数组A与数组B中所有的元素全都存入数组C中，且按从小到大排序 (注意：序列中相同的数全部保留并不计排列顺序)。例如，设数组A中有元素：2，5， 6，7，9；数组B中有元素2，3，4，7：则数组C中将有元素：2，2，3，4，5，6，7， 7， 9。
【流程图】
正确答案：(1)1 (2)A(i) (3)B(j) (4)i (5)j (6)B(j) (7)A(i) (8)j (9)i
(1)1 (2)A(i) (3)B(j) (4)i (5)j (6)B(j) (7)A(i) (8)j (9)i 解析：这是最常见的一种合并排序方法。为对较大的序列进行排序，先将其分割成容量相当的几个部分，分别进行排序，最后再合并在一起。当然，这些排序要么都是升序，要么都是降序。本题全部是按升序排序的。
例如，为了将整副扑克牌按升序进行排序，先将其分割成两个部分(数量大致相当)，对每个部分完成升序排序后，就形成了两叠已排序的牌。如何将其合并呢?办法如下。
每次都比较各叠最上面的两张牌，取出比较小的，放入新堆，再继续比较。直到其中一堆空了，就将另一堆剩余的牌逐张放入新堆。新堆就是合并后的已完成排序的序列。
在数据排序时，遇到相同的数比较时，任取一个就可以了。
对本题来说，i、j、k是数组A、B、C的下标，初始时，都应该是1。因此，空(1)处应填写1。
将A(i)与B(j)进行比较后，如果A(i)≤B(j)，那么应该将A(i)→C(k)。这是升序的要求。因此，空(2)处应填A(i)。如果A(i)＞B(j)，则应将B(j)→C (k)。因此，空(3)处应填B(j)。
在A(i)→C(k)后，i应增加1，为下次取A(i)再比较做准备(k也需要增加1，为下次存入C(k)做准备)。这时，需要比较数组A是否已经取完，即判断i＞M是否成立。如果i＞M，则表示数组A中的元素已经全部取出，需要将数组B中剩余的元素逐个移入C(k)。因此，空(4)处应填i，空(6)处应填B(j)。数组B处的元素何时移完呢?这就需要判断i＞N是否成立。因此，空(8)处应填j。
同样，空(3)处将B(j)存入C(k)，直到，j＞N时数组B中的元素取完。此时，需要将数组A中剩余的元素逐个移入C(k)，直到i＞M时全部完成。因此，空(5)处应填j，空(7)处应填A(i)，空(9)处应填i。 -
第2题：
阅读下列说明，回答问题1至问题2，将解答填入答题纸的对应栏内。
[说明]
如图10-4所示是电子商务系统平台结构示意图。
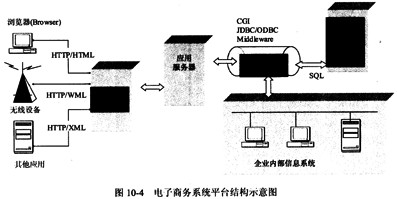
请把空缺的地方填写完整。
正确答案：(1)接口中间层。 (2)Web服务器。 (3)数据库服务器。
(1)接口中间层。 (2)Web服务器。 (3)数据库服务器。 -
第3题：
阅读以下说明和流程图，回答问题1-2，将解答填入对应的解答栏内。
[说明]
下面的流程图采用欧几里得算法，实现了计算两正整数最大公约数的功能。给定正整数m和 n，假定m大于等于n，算法的主要步骤为：
(1)以n除m并令r为所得的余数；
(2)若r等于0，算法结束；n即为所求；
(3)将n和r分别赋给m和n，返回步骤(1)。
[流程图]
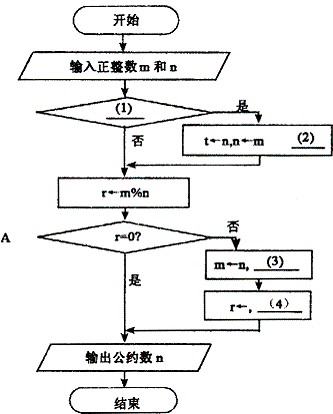
[问题1] 将流程图中的(1)～(4)处补充完整。
[问题2] 若输入的m和n分别为27和21，则A中循环体被执行的次数是(5)。
正确答案：[问题1] (1) n＞m或nm或其它等效形式 (2) m←t (3) n←r (4) m%n [问题2] (5) 1
[问题1] (1) n＞m或nm或其它等效形式 (2) m←t (3) n←r (4) m%n [问题2] (5) 1 解析：(1)～(2)当n的值大于(等于)m时，应交换两者的值，再使用欧几里得算法；
(3)～(4)略；
(5)m，n和r在执行循环A前后的值分别为：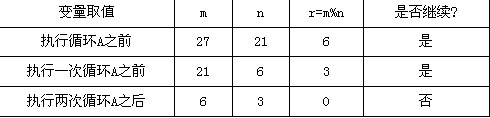
-
第4题：
阅读下列说明，回答问题1至问题2，将解答填入答题纸的对应栏内。
[说明]
小舟很喜欢网上购物，不但自己经常上网买东西，还自己经营了一家商业网站，大到卖电器，衣物，小到可以和注册用户交换东西等等。
图2-15是网上小舟经营的网站的购物流程图，请把空缺的部分补充完整。
正确答案：①购买过程②验证过程③银行。
①购买过程②验证过程③银行。 -
第5题：
阅读以下说明和流程图，回答问题，并将解答填入对应栏内。
【说明】
求解约瑟夫环问题。算法分析：n个士兵围成一圈，给他们依次编号，班长指定从第w个士兵开始报数，报到第s个士兵出列，依次重复下去，直至所有士兵都出列。
【流程图】
【问题】
将流程图中的(1)～(5)处补充完整。
正确答案：(1)L[i].nextp=1 (2) k=w-1 (3) count!=n (4) ++I (5) ++count
(1)L[i].nextp=1 (2) k=w-1 (3) count!=n (4) ++I (5) ++count -
第6题：
阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏内。 【说明】 设有整数数组A[1：N]（N>1），其元素有正有负。下面的流程图在该数组中寻找连续排列的若干个元素，使其和达到最大值，并输出其起始下标K、元素个数L以及最大的和值M。 例如，若数组元素依次为3，-6，2，4，-2，3，-1，则输出K=3，L=4,M=7。该流程图中考察了A[1：N]中所有从下标i到下标j（j≥i）的各元素之和S，并动态地记录其最大值M。
【流程图】
注：循环开始框内应给出循环控制变量的初值和终值，默认递增值为1，格式为：循环控制变量=初值，终值正确答案：（1）i，N
（2）S+A[j]
（3）S
（4）j-i+1
（5）S
-
第7题：
阅读以下说明和Java程序，填补代码中的空缺(1)～(6)，将解答填入答题纸的
对应栏内。
【说明】
很多依托扑克牌进行的游戏都要先洗牌。下面的Java代码运行时先生成一副扑克
牌，洗牌后再按顺序打印每张牌的点数和花色。
【Java代码】
正确答案：
本题考查Java语言程序设计的能力，涉及类、对象、方法的定义和相关操作。要求考生根据给出的案例和代码说明，认真阅读，理清程序思路，然后完成题目。先考查题目说明。本题目中涉及到扑克牌、牌桌、玩家等类以及洗牌和按点数排序等操作。根据说明进行设计。Card类内定义了两个static枚举类型，Face枚举扑克牌点数，Suit枚举扑克牌花色。Card类有两个枚举类型的属性，face和suit，而且值不再变化，故用final修饰。在使用构造方法publicCard(Faceface，Suitsuit)新建一个Car:d的对象时，所传入的参数指定face和suit这两个属性值。因为参数名称和属性名称相同，所以用this前缀区分出当前对象。在类Card中包含方法getFace（）和getSuit（），分别返回当前对象的face和suit属性值。getCard（）方法返回string来表示一张牌，包括扑克牌点数和花色。牌桌类Deckofcands包含持有Card类型元素的List类型对象的声明List，用以存储牌。List是Java中的一种集合接口，是Collection的子接口。构造方法中用Card对象填充牌桌并进行洗牌。先用Card对象填充牌桌，即创建52个Card对象加入deck数组，表示牌桌上一副牌(52张)。然后洗牌，即将数组中的Card对象根据花色和点数随机排列，使用集合工具类Collechons中的shuffle方法，对以List类型表示的deck数组进行随机排列。Collectians是Java集合框架中两个主要工具类之一，用以进行集合有关的操作。printCards（）方法将所有Card对象打印出来，按4列显示52张牌。每张拍的打印用list.get(i)获得list表示的deck中的第i个Card对象，然后进一步调用此对象的getCard（）方法，得到String表示的当前一张牌。玩家类中包括启动发牌洗牌等操作，主入口方法main中实现创建牌桌对象，并调用按4列显示52张牌。在main（）中，先初始化Deckofcards类的对象player，即生成一个牌桌：Deckofcardsplayer=newDeckofcards()并发牌，即调用player的printCards()方法，实现按4列显示52张牌打印一副扑克牌中每张牌的点数和花色。在pnntCards()方法体内部，用list调用每个数组元素，井为每个数组元素调用getCard()返回当前对象所表示一张牌的花色和点数。用格式化方法进行打印，即：因此，主(1)和(2)需要表示当前对象的this.；空(3)需要牌桌上纸牌对象，并将数组元素下标加1，即数组元素deck[count++]；空(4)也需要用list对象获得纸牌对象的字符串表示，即list后的get(1)getCard（）；空(5)处为创建DeckOf℃ards类的对象指针player的newDeckOfCards（）；空(6)需要用对象player调用打印所有纸牌的printCards（）函数，即player.。试题六参考答案(l)this(2)this.(3)deck[count++]或等价表示(4)get(i)getCard()(5)newDeckOfCards(）(6)player. -
第8题：
试题一（共 15 分）
阅读以下说明和流程图，填补流程图中的空缺（1）～（9） ，将解答填入答题纸的对应栏内。
[说明]
假设数组 A 中的各元素 A(1)，A(2) ，…，A(M)已经按从小到大排序（M≥1） ；数组 B 中的各元素 B(1)，B(2)，…，B(N)也已经按从小到大排序（N≥1） 。执行下面的流程图后， 可以将数组 A 与数组 B 中所有的元素全都存入数组 C 中， 且按从小到大排序 （注意：序列中相同的数全部保留并不计排列顺序） 。例如，设数组 A 中有元素：2，5，6，7，9；数组B 中有元素：2，3，4，7；则数组 C 中将有元素：2，2，3，4，5，6，7，7，9。
[流程图]
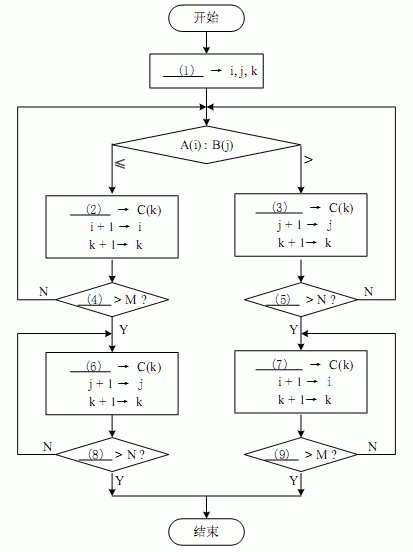正确答案：
-
第9题：
阅读下列说明和流程图，填补流程图中的空缺（1）~（9），将解答填入答题纸的对应栏内。【说明】假设数组A中的各元素A⑴，A (2)，…，A (M)已经按从小到大排序(M>1):数组B中的各元素B(1) , B (2) . B (N)也已经按从小到大排序(N≥1)。执行下面的流程图后，可以将数组A与数组B中所有的元素全都存入数组C中，且按从小到大排序(注意：序列中相同的数全部保留并不计排列顺序)。例如，设数组A中有元素： 2,5,6,7,9;数组B中有元素： 2,3,4,7;则数组C中将有元素： 2,2,3,4,5,6,7，7,9.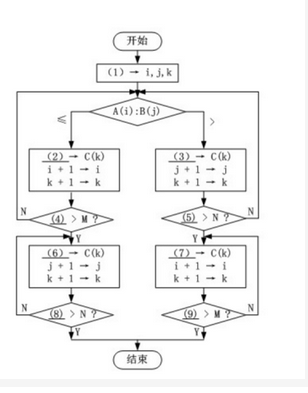
答案：解析：(1)1 (2)A (i) (3) B (j)⑷ i (5)J(6) B (j)(7) A (i)(8) j(9) i -
第10题：
阅读说明和流程图，填补流程图中的空缺（1）?（5），将答案填入答题纸对应栏内。【说明】本流程图用于计算菲波那契数列{a1=1，a2=1，…,an=an-1+an-2!n=3,4,…}的前n项（n>=2) 之和S。例如，菲波那契数列前6项之和为20。计算过程中，当前项之前的两项分别动态地保存在变量A和B中。【流程图】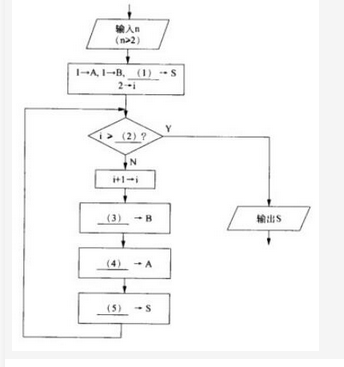
答案：解析：（1）2或A+B（2）n（3）A+B（4）B-A（5）S+B
【解析】
菲波那契数列的特点是首2项都是1，从第3项开始，每一项都是前两项之和。该数列的前几项为1，1，2, 3，5，8，…。在流程图中，送初始值1—A，2—B后，显然前2项的和S应等于2,所以（1）处应填2 (或A+B)。此时2→i (i表示动态的项编号），说明已经计算出前2项之和。接着判断循环的结束条件。显然当i=n时表示已经计算出前n项之和，循环可以结束了。因此（2）处填n。判断框中用“>”或“≥”的效果是一样的，因为随着i的逐步增1，只要有i=n结束条件就不会遇到i>n的情况。不过编程的习惯使循环结束条件扩大些，以防止逻辑出错时继续循环。接下来i+1→i表示数列当前项的编号增1，继续往下计算。原来的前两项值（分别在变量A和B中）将变更成新的前两项再放到变量A和B中。
首先可以用A+B—B实现（原A) + (原B)—(新B)，因此（3）处填A+B。为了填新A值（原来的B值)，不能用B—A，因为变量B的内容已经改变为（原A) + (原B)，而B-A正是（（原A) + (原B))-(原A)=(原B)，因此可以用B-A—A来实现新A的赋值。这样，（4）处填B-A。最后应是前n项和值的累加（比原来的S值增加了新B值)，所以（5）处应填S+B。填完各个空后，最好再用具体的数值来模拟流程图走几个循环检查所填的结果（这是防止逻辑上出错的好办法）。 -
第11题：
第一题 阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏内。
【说明】
对于大于1的正整数n，(x+1)n可展开为
问题：1.1 【流程图】
注：循环开始框内应给出循环控制变量的初值和终值，默认递增值为1。
格式为：循环控制变量=初值，终值，递增值。答案：解析：（1）2，n，1
（2）A[k]
（3）k-1，1，-1
（4）A[i]+A[i-1]
（5）A[i]
【解析】
（1）（3）空为填写循环初值终值和递增值，题目中给出的格式为循环控制变量=初值，终值，递增值。按照题意，实质为求杨辉三角。如下图：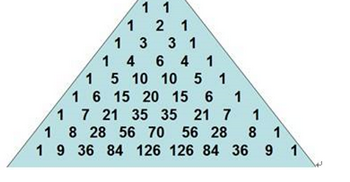
-
第12题：
阅读以下说明和流程图，填写流程图中的空缺，将解答填入答题纸的对应栏内。【说明】设[a1b1],[a2b2],...[anbn]是数轴上从左到右排列的n个互不重叠的区间（a1
答案：解析：1.A2.ai3.bi4.A 、B5.B
【解析】
若A≤ai则输出A，反之输出ai。若A≤bi不满足则输出bi，依次类推。 -
第13题：
阅读以下说明和流程图，填补流程图中的空缺(1)～(5)，将解答填入对应栏内。
[说明]
下面的流程图旨在统计指定关键词在某一篇文章中出现的次数。
设这篇文章由字符A(0)，…，A(n-1)依次组成，指定关键词由字符B(0)，…，B(m-1)依次组成，其中，n＞m≥1。注意，关键词的各次出现不允许有交叉重叠。例如，在“aaaa”中只出现两次“aa”。
该流程图采用的算法是：在字符串A中，从左到右寻找与字符串B相匹配的并且没有交叉重叠的所有子串。流程图中，i为字符串A中当前正在进行比较的动态予串首字符的下标，j为字符串B的下标，k为指定关键词出现的次数。
[流程图]
正确答案：0-k i+j i+m i+1 i
0-k i+j i+m i+1 i 解析：本题考查用流程图描述算法的能力。
在文章中查找某关键词出现的次数是经常碰的问题。例如，为了给文章建立搜索关键词，确定近期的流行语，迅速定位文章的某个待修改的段落，判断文章的用词风格，甚至判断后半本书是否与前半本书是同一作者所写(用词风格是否一致)等，都采用了这种方法。
流程图最终输出的计算结果K就是文章字符串A中出现关键词字符串B的次数。显然，流程图开始时应将K赋值0，以后每找到一处出现该关键词，就执行增1操作K=K+1。
因此(1)处应填0→K。
字符串A和B的下标都是从0开始的。所以在流程图执行的开始处，需要给它们赋值0。接下来执行的第一个小循环就是判断A(i)，A(i+1)，…，A(i+j-1)是否完全等于B(0)，B(1)，…，B(m-1)，其循环变量j=0，1，…，m-1。只要发现其中对应的字符有一个不相等时，该小循环就结束，不必再继续执行该循环。因此，该循环中继续执行的判断条件应该是A(i+j)=B(j)且jm。只要遇到A(i+j)≠B(j)或者j=m(关键词各字符都己判断过)就不再继续执行该循环了。因此流程图的(2)处应填州i+j。
许多考生在(2)处填i，当j增1变化后，仍然使用A(i)进行比较就不对了。因此，在检查循环程序段时应多走查一次循环。
如果(2)处整体的判断条件不成立，则该判断关键词的小循环结束。此时可能有两种情况。一是在j=0，1，…，m-1时全都成立A(i+j)=B(j)(找到了一处关键词)，直到j=m时才结束小循环；二是在jm时就发现了字符不等的情况，这说明此处并不出现关键词。因此流程图中用jm来区分找到与没有找到关键词的两种情况。
对于j=m，已找到一处关键词的情况，显然应该执行k=k+1，对关键词出现次数的变量k进行增1计算。同时，为了继续进行以后的判断，应将字符串A的下标i右移m(这是因为题中假设关键词的出现不允许重叠)。因此(3)处应填写i+m，表示应该从已出现的关键词后面开始再继续进行判断。由于此时的j=m，书写i+j的答案也是正确的，但这不是程序员的好习惯，因为这不符合逻辑思维的顺势，在程序不断修改的过程中容易出错。不少考生在(3)处填写i+1，这意味着下次判断关键词将从A(i+1)开始，这就使关键词的出现有可能发生部分重叠的现象。
流程图中，对于jm的情况，表示刚才判断关键词时并非各个字符都完全相同，也就是说，刚才的判断结论是此处并没有出现关键词。即A(i)开始的子串并不是关键词。因此，下次判断关键词应该以A(i+1)开始，即(4)处应填i+1。
在下次判断关键词之前还应该判断是否全文已经判断完。最后一次小循环判断应该是对A(n-m)，A(n-m+1)，…，A(n-1)的判断。下标n-m来自从n-1倒数m个数。可以先试验写出A(n-m)，A(n-m+1)，…，A(n-1)，再判断其个数是否为m。经检查，个数为(n-1)-(n-m)+1=m个，所以这是正确的。也可以用例子来检查次数是否正确。检查次数是程序员的基本功，数目的计算很容易少一个或多一个。
既然最后一次判断关键词应该是对A(n-m)，A(n-m+1)，…，A(n-1)的判断，即对i=n-m进行的小循环判断，所以当i＞n-m时就应该停止大循环，停止再查找关键词了。
-
第14题：
阅读下列说明，回答问题1至问题2，将解答填入答题纸的对应栏内。
[说明]
电子商务系统的外部社会环境如图10-5所示。
请把空缺的地方填写完整。
正确答案：(1)原料供应商。 (2)企业电子商务系统。 (3)消费者。
(1)原料供应商。 (2)企业电子商务系统。 (3)消费者。 -
第15题：
阅读以下说明，回答问题，将解答填入对应的解答栏内。
. [说明] 请完成流程图以描述在数据A(1)至A(10)中求最大数和次大数的程序的算法。并将此改成PAD图。该算法的流程图如下图：
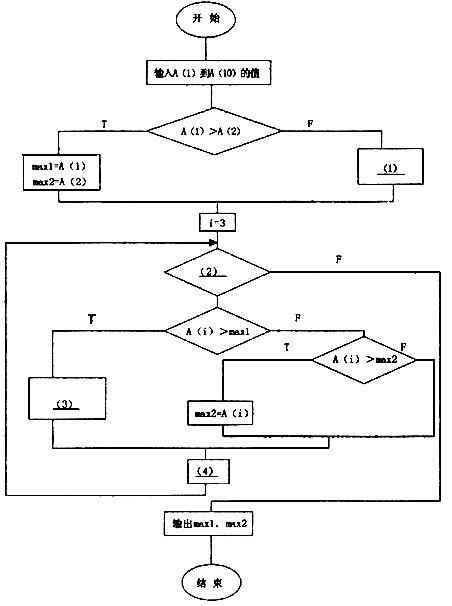正确答案：(1)max2 =A(1) mex1 =A(2) (2)i< =10 (3)max1 =A(i)1 max2 = max1 (4)i=i+1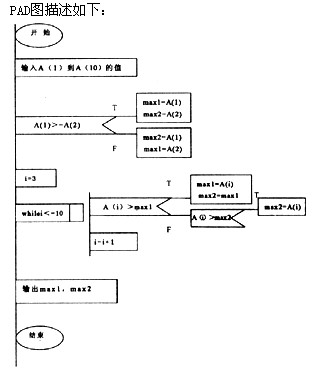
(1)max2 =A(1) mex1 =A(2) (2)i< =10 (3)max1 =A(i)1 max2 = max1 (4)i=i+1 解析：本题的算法思想是：先输入A(1)到A(10)的值，然后判断前两个数的大小。用变量max1存储最大数，用变量max2．存储次大数。然后逐个读入数据，分别和max1，max2比较，保证最大的存入max1，次大的存入max2。
-
第16题：
阅读以下说明和流程图，将应填入(n)处的字句写在对应栏内。
[说明]
下面的流程图用于计算一个英文句子中最长单词的长度(即单词中字母个数)MAX。假设该英文句子中只含字母、空格和句点“.”，其中句点表示结尾，空格之间连续的字母串称为单词。
[流程图]
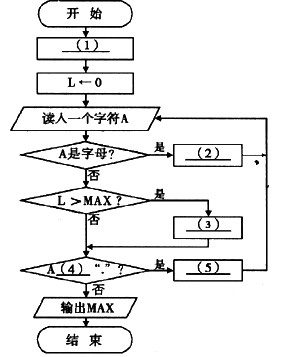正确答案：(1)MAX←0 (2)←L+1 (3)MAX←L (4)≠ (5)L←0
(1)MAX←0 (2)←L+1 (3)MAX←L (4)≠ (5)L←0 解析：本题用到的三个变量及其作用分别为：A，存放输入的一个字符；MAX，存放当前为止最长单词的长度；L，存放当前单同的长度。
(1)使用变量MAX应先赋予初值，由上下文知其初值为0；
(2)读取当前单词时，每读人一个字母，单词长度值L应增1；
(3)当前单词长度L比MAX时，应更新MAX的值；
(4)若当前字符不是句点，应当继续读取字符；
(5)读取下一个单词前，应当重置L的值。 -
第17题：
阅读下列说明和流程图，将应填入(n)处的语句写在对应栏内。
【说明】
设学生(学生数少于50人)某次考试的成绩按学号顺序逐行存放于某文件中，文件以单行句点“.”为结束符。下面的流程图用于读取该文件，并把全部成绩从高到低排序到数组B[50]中。
【流程图】
正确答案：(1)B[0]←a (2)i←0 (3)a="." (4)aB[j] (5)j--
(1)B[0]←a (2)i←0 (3)a="." (4)aB[j] (5)j-- 解析：本题考查用程序流程图来描述排序。
题目要求将文件中学生的成绩读出，并把全部成绩从高到低排序到数组B[50]中。这里面涉及两个问题，第一是从文件中读数，文件中的数据是以单行句点“.”为结束符的，在未读到此符号前，应该将继续取数据。第二是排序，每取到一个学生的成绩都要与数组的学生成绩比较，按照从高到低的顺序在数组中找到合适的位置存放。下面来具体分析流程图。
第(1)空在条件判断为假的情况下执行流程中，如果条件为假说明从文件中取到的数据是学生成绩。从程序流程图中可以看到，从文件中读的数据存放在变量a中，而此空是第一次取数据，应该存放数组B的第一个位置，因此此空答案为B[0]←a。
第(2)空是紧接着第(1)空来的，在上面已经把从文件中读到的第一个数存放到了数组中，接下来应该处理数组的下标问题，从后面的流程中可以推断出变量i是存放数组当前下标的，而且没有初值，那么此空的任务应该是用来给变量i赋一个初值，而对数组的操作应该从头开始，因此此空答案为i←0。
第(3)空是循环的判断条件，如果条件成立则结束，在这之前又对文件进行了一次读数，根据我们上面的分析只有在读到了结束符时程序才结束，那么此空肯定是判断从文件中读到的数据是否为结束符，因此此空答案为a="."?。
第(4)空也是一个循环的判断条件，如果条件成立，则将取到的数存放到数组的当前下标位置；如果不成立，则循环找到合适的位置再存放。从这里我们不难推断出，流程图中是将从文件取到的成绩与当前数组中的最小成绩进行比较的，而当前数组中的最小成绩存放在位置j中，因此此空答案为aB[i]?。
第(5)空在循环体中，这个循环的作用是为当前从文件中读到的成绩在已经排好序的数组元素中找到合适的位置，找到了就要插入，数组中的元素是按从大到小排列的，在查找合适位置时是从后往前依次比较，因此此空的任务应该是将数组的下标往前移动，所以此空答案为“i--”。 -
第18题：
?????? 阅读以下说明和流程图，填补流程图中的空缺(1)～(5)，将解答填入答题纸的
对应栏内。
【说明】
本流程图旨在统计一本电子书中各个关键词出现的次数。假设已经对该书从头到尾
依次分离出各个关键词{A(i)li=l，…，n}(n＞1)}．其中包含了很多重复项，经下面的流程
处理后，从中挑选出所有不同的关键词共m个{K（j）[j=l，…，m}，而每个关键词K（j）出现的次数为NK（j）．j=l，…，m。
??????
正确答案：
??流程图中的第1框显然是初始化。A(1)→K(1)意味着将本书的第1个关键词作为选出的第1个关键词。1→NK(1)意味着此时该关键词的个数置为1。m是动态选出的关键词数目，此时应该为1，因此(1)处应填1。?本题的算法是对每个关键词与已选出的关键词进行逐个比较。凡是遇到相同的，相??应的计数就增加1；如果始终没有遇到相同关键词的，则作为新选出的关键词。流程图第2框开始对i=2,n循环，就是对书中其他关键词逐个进行处理。流程图第3框开始j=l，m循环，就是按已进出的关键词依次进行处理。接着就是将关键词A(i)与选出的关键词K(j)进行比较。因此(2)处应填K(j)。如果A(i)=K(j)，则需要对计数器NK(j)增1．即执行NK(j)+1→NK(j)。因此(3)处应填NK(j)+I→NK(j)。执行后，需要跳出j循环，继续进行i循环，即根据书中的下一个关键词进行处理。如果A(i)不等于NK(j)，则需要继续与下个NK(j)进行比较，即继续执行j循环。如果直到j循环结束仍没有找到匹配的关键词，则要将该A(i)作为新的已选出的关键词。因此，应执行A(i)→K(m+1)以及m+l→m。更优的做法是先将计数器m增1，再执行A（j)→K(m)。因此(4)处应填m+l→m，(5)处应填A(i)。试题一参考答案(1)1(2)K(j)(3)Nk(j)+I→NK(j)或NK(j)十十或等价表示(4)m+l→m或m++或等价表示(5)A(i)?? -
第19题：
●试题一
阅读下列说明和流程图，将应填入(n)的字句写在答题纸的对应栏内。
【说明】
下列流程图(如图4所示)用泰勒(Taylor)展开式
sinx=x-x3／3!+x5／5!-x7／7!+…+(-1)n×x 2n+1／(2n+1)!+…
【流程图】
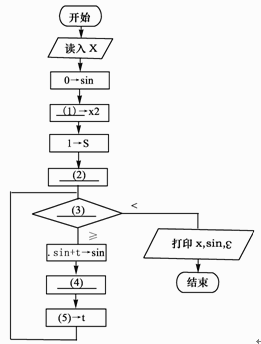
图4
计算并打印sinx的近似值。其中用ε(>0)表示误差要求。
正确答案：
●试题一【答案】(1)x*x(2)x->t(3)|t|∶ε(4)s+2->s(5)(-1)*t*x2／(s*(s-1))【解析】该题的关键是搞清楚几个变量的含义。很显然变量t是用来保存多项式各项的值，变量s和变量x2的作用是什么呢?从流程图的功能上看，需要计算1!、3!、5!，……，又从变量s的初值置为1可知，变量s主要用来计算这此数的阶乘的，但没有其他变量用于整数自增，这样就以判断s用来存储奇数的，即s值依次为1、3、5，……。但x2的功能还不明确，现在可以不用管它。(2)空的作用是给t赋初值，即给它多项式的第一项，因此应填写"x->t"。(3)空处需填写循环条件，显然当t的绝对值小于ε(>0)就表示已经达到误差要求，因此(3)空应填入"|t|∶ε"。由变量s的功能可知，(4)空应当实现变量s的增加，因此(4)空应填入"s+2->s"。(5)空应当是求多项式下一项的值，根据多项式连续两项的关系可知，当前一项为t时，后一项的值为(-1)*t*x*x／(s*(s-1))。但这样的话，每次循环都需要计算一次x*x，计算效率受到影响，联想到变量x2还没用，这时就可以判断x2就是用来存储x*x的值，使得每次循环者少进行一次乘法运算。因此(1)空处应填入"x*x"，(5)空处应填入"(-1)*t*x2／(s*(s-1))"。 -
第20题：
阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏内。
[说明]
两个包含有限个元素的非空集合A、B的相似度定义为|A∩B|/|A∪B|，即它们的交集大小(元素个数)与并集大小之比。
以下的流程图计算两个非空整数集合(以数组表示)的交集和并集，并计算其相似度。已知整数组A[1:m]和B[1:n]分别存储了集合A和B的元素(每个集合中包含的元素各不相同)，其交集存放于数组C[1:s]，并集存放于数组D[1:t]，集合A和B的相似度存放于SIM。
例如，假设A={1，2，3，4}，B={1，4，5，6}，则C={1，4)，D={1，2，3，4，5，6}，A与B的相似度SIM=1/3。
[流程图]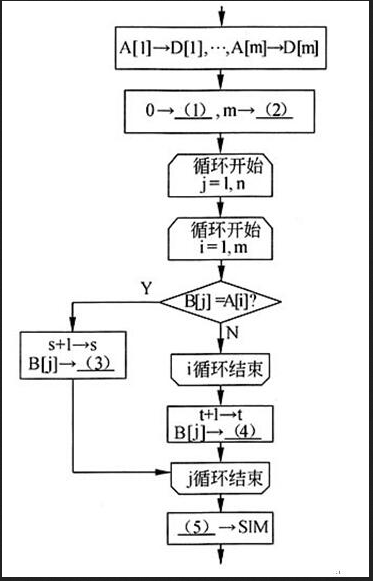
答案：解析：s
t
C[s]
D[t]
s/t
【解析】
本题考查程序处理流程图的设计能力。
首先我们来理解两个有限集合的相似度的含义。两个包含有限个元素的非空集合A、B的相似度定义为它们的交集大小(元素个数)与并集大小之比。如果两集合完全相等，则相似度必然为1(100%)；如果两集合完全不同(没有公共元素)，则相似度必然为0；如果集合A中有一半元素就是集合B的全部元素，而另一半元素不属于集合B，则这两个集合的相似度为0.5(50%)。因此，这个定义符合人们的常理性认识。
在大数据应用中，经常要将很多有限集进行分类。例如，每天都有大量的新闻稿。为了方便用户检索，需要将新闻稿分类。用什么标准来分类呢?每一篇新闻稿可以用其中所有的关键词来表征。这些关键词的集合称为这篇新闻稿的特征向量。两篇新闻稿是否属于同一类，依赖于它们的关键词集合是否具有较高的相似度(公共关键词个数除以总关键词个数)。搜索引擎可以将相似度超过一定水平的新闻稿作为同一类。从而，可以将每天的新闻稿进行分类，就可以按用户的需要将某些类的新闻稿推送给相关的用户。
本题中的集合用整数组表示，因此，需要规定同一数组中的元素各不相同(集合中的元素是各不相同的)。题中，整数组A[1:m]和B[1:n]分别存储了集合A和B的元素。流程图的目标是将A、B中相同的元素存放入数组C[1:s](共s个元素)，并将A、B中的所有元素(相同元素只取一次)存放入数组D[1:t](共t个元素)，最后再计算集合A和B相似度s/t。
流程图中的第一步显然是将数组A中的全部元素放入数组D中。随后，只需要对数组B中的每个元素进行判断，凡与数组A中某个元素相同时，就将其存入数组C；否则就续存入数组D(注意，数组D中已有m个元素)。这需要对j(遍历数组B)与i(遍历数组A)进行两重循环。判断框B[j]=A[i]成立时，B[j]应存入数组C；否则应继续i循环，直到循环结束仍没有相等情况出现时，就应将B[i]存入数组D。存入数组C之前，需要将其下标s增1；存入数组D之前，需要将其下标t增1。因此，初始时，应当给i赋0，使数组C的存数从C[1]开始。从而，(1)处应填s，(3)处应填C[s]。而数组D是在已有m个元素后续存，所以，初始时，数组D的下标t应当是m，续存是从D[m+1]开始的。因此，(2)处应填t，(4)处应填D[t]。
两重循环结束后，就要计算相似度s/t，将其赋予SIM，因此(5)处应填s/t。 -
第21题：
阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏内。
[说明]
本流程图旨在统计一本电子书中各个关键词出现的次数。假设已经对该书从头到尾依次分离出各个关键词{A(i)|i=1,…,n}(n＞1)}，其中包含了很多重复项，经下面的流程处理后，从中挑选出所有不同的关键词共m个{K(j)|j=1,…,m}，而每个关键词K(j)出现的次数为NK(j),j=1,…,m。
[流程图]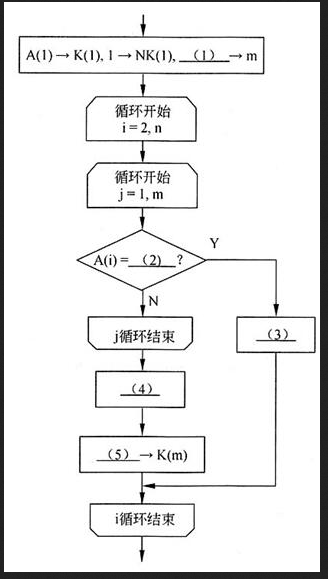
答案：解析：1
K(j)
NK(j)+1→NK(i) 或NK(j)++ 或等价表示
m+1→m或m++ 或等价表示
A(i)
【解析】
流程图中的第1框显然是初始化。A(1)→K(1)意味着将本书的第1个关键词作为选出的第1个关键词。1→NK(1)意味着此时该关键词的个数置为1。m是动态选出的关键词数目，此时应该为1，因此(1)处应填1。
本题的算法是对每个关键词与已选出的关键词进行逐个比较。凡是遇到相同的，相应的计数就增加1；如果始终没有遇到相同关键词的，则作为新选出的关键词。
流程图第2框开始对i=2,n循环，就是对书中其他关键词逐个进行处理。流程图第3框开始j=1，m循环，就是按己选出的关键词依次进行处理。
接着就是将关键词A(i)与选出的关键词K(j)进行比较。因此(2)处应填K(j)。
如果A(i)=K(i)，则需要对计数器NK(j)增1，即执行NK(j)+1→NK(j)。因此(3)处应填NK(j)+1→NK(j)。执行后，需要跳出j循环，继续进行i循环，即根据书中的下一个关键词进行处理。
如果A(i)不等于NK(j)，则需要继续与下个NK(j)进行比较，即继续执行j循环。如果直到j循环结束仍没有找到匹配的关键词，则要将该A(i)作为新的已选出的关键词。因此，应执行A(i)→K(m+1)以及m+1→m。更优的做法是先将计数器m增1，再执行A(i)→K(m)。因此(4)处应填m+1→m，(5)处应填A(i)。 -
第22题：
试题（15 分）阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏 内。【说明】设有整数数组 A[1：N]（N>1），其元素有正有负。下面的流程图在该数组 中寻找连续排列的若干个元素，使其和达到最大值，并输出其起始下标 K、元素 个数 L 以及最大的和值 M。例如，若数组元素依次为 3，-6，2，4，-2，3，-1，则输出 K=3，L=4,M=7。 该流程图中考察了 A[1：N]中所有从下标 i 到下标 j（j≥i）的各元素之和 S，并动态地记录其最大值 M。【流程图】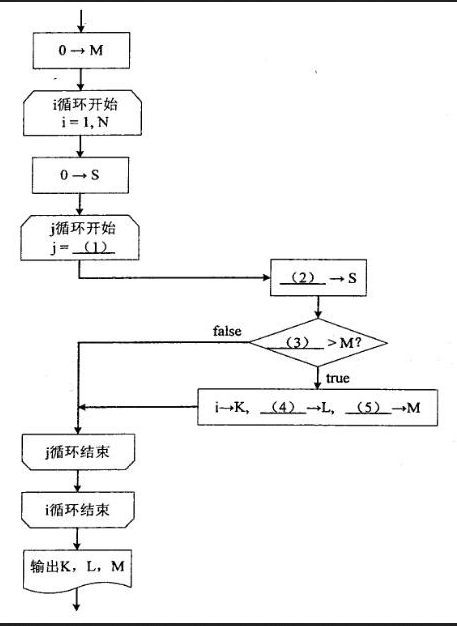
注：循环开始框内应给出循环控制变量的初值和终值，默认递增值为 1，格式为：循环控制变量=初值，终值答案：解析：1、j=i+1
2、S+A[j]
3、S
4、j-i+1
5、S -
第23题：
阅读下列说明，补充（1）-（9），将解答填入答题纸的对应栏内。
答案：解析：